Méthode du dynamique et du funiculaire

Exemple de construction d'un dynamique et d'un funiculaire (deux tracés à partir de deux points différents)

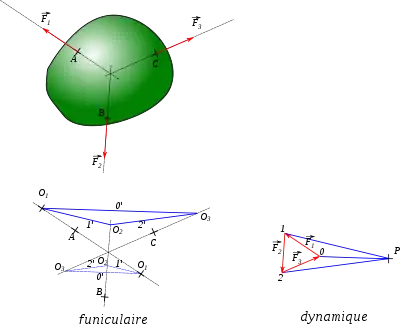
Considérons un problème de statique résolu (toutes les forces sont connues). La première étape consiste à tracer le dynamique, c'est-à-dire à dessiner à une échelle donnée les n forces mises bout à bout (les forces sont les vecteurs rouge dans la figure ci-contre). On a donc un polygone fermé ; bien que cela ne soit pas une nécessité, on prend les forces en progressant dans un sens, par exemple de gauche à droite, ce qui permet d'éviter que le funiculaire soit un polygone croisé. On numérote les sommets du dynamique, de 0 à n-1, dans le sens des flèches des vecteurs.

Nous considérons ci-contre un exemple avec trois forces ${\displaystyle {\vec {\mathrm {F} }}_{1}}$, ${\displaystyle {\vec {\mathrm {F} }}_{2}}$ et ${\displaystyle {\vec {\mathrm {F} }}_{3}}$.

Puis, on écrit un tableau de deux lignes :

• la première ligne contient les noms des forces dans l'ordre donné par le sens des flèches ;
• la deuxième ligne indique les sommets que relient chaque force : 0 → 1, 1 → 2, …, n-1 → 0.

Forces	${\displaystyle {\vec {\mathrm {F} }}_{1}}$	${\displaystyle {\vec {\mathrm {F} }}_{2}}$	${\displaystyle {\vec {\mathrm {F} }}_{3}}$
Sommets	0 → 1	1 → 2	2 → 0

On prend un point quelconque ; par convention, on le prend hors de ce polygone, à droite ou à gauche du polygone. Pour que le tracé du funiculaire soit précis et compact, il faut le prendre suffisamment loin du polygone, et sur une ligne horizontale passant à peu près au centre du polygone ; cela permet d'avoir des droites polaires (voir plus loin) peu inclinées. Ce point est appelé pôle et habituellement noté P, ou S lorsque la lettre P est déjà utilisée.

Ensuite, on relie le pôle aux sommets ; les segments de droite ainsi formés, les droites polaires (en bleu sur la figure ci-contre), portent le nom des sommets auxquels ils sont attachés.

Puis on trace le polygone funiculaire : sur le dessin du système, on prend un point arbitraire O₁ quelconque de la ligne d'action de la première force du tableau (celle reliant le sommet 0 au sommet 1 du dynamique), et on trace un segment de droite parallèle à la droite polaire 1 que l'on arrête sur la ligne d'action de la deuxième force. Ce segment est appelé 1’ (1 est le sommet du dynamique commun aux forces dont les lignes d'action sont reliées par 1’), et le point d'arrêt est appelé O₂. On part de O₂ et l'on construit 2’, le segment parallèle au segment 2 du dynamique et s'arrêtant sur la ligne d'action de la troisième force du tableau (2 est le sommet du dynamique commun aux forces dont les lignes d'action sont reliées par 2’). Et ainsi de suite.

On obtient ainsi un polygone fermé.

Résumé synthétique de la méthode : tout segment du funiculaire (parallèle à un rayon polaire du dynamique) joint les deux droites d'action des forces successives dont le point commun génère le rayon polaire considéré.

Le funiculaire est en fait un câble dont les angles sont sur les droites d'action des forces.

Pour qu'un solide soit en équilibre, il faut

1. Que la somme des forces soit nulle, et
2. Que la somme des moments de forces par rapport à un point quelconque soit nulle.

Ce qui importe pour le moment, c'est la hauteur du point considéré à la droite portant la force, dite ligne d'action de la force ; c'est la longueur du segment perpendiculaire à la ligne d'action passant par le point. Dans le cadre de la statique, on peut donc placer le point d'application de la force n'importe où sur cette droite d'action (ceci devient faux lorsque l'on considère les déformations ou les notions d'équilibre stable ou instable).

Le funiculaire consiste à remplacer l'objet étudié par un câble qui est en équilibre sous l'action des mêmes forces, d'où le terme « funiculaire ». Les segments joignant le pôle aux angles du dynamique sont les forces qui s'exercent dans ces segments de câble (traction) :

• chaque angle du funiculaire est à l'équilibre sous l'effet de trois forces (la force extérieure et les forces des deux segments de câble), le dynamique de ce point est donc un triangle dont un côté est la force extérieure et les deux autres sont parallèles aux segments de câble ;
• les différents dynamiques ainsi obtenus ont des côtés communs, puisque les forces aux extrémités des segments de câble sont égales et opposées, donc de même direction et de même longueur ;
• en assemblant les différents dynamiques, à l'instar d'un tangram, on obtient le dynamique final avec les droites polaires.

Exemple d'utilisation de la méthode pour résoudre un problème. La détermination de la ligne de fermeture (LF) sur le funiculaire permet de déterminer la longueur des vecteurs force sur le dynamique.

L'intérêt de cette construction est de pouvoir déterminer des forces inconnues et/ou des lignes d'action inconnues. Dans ce cas-là, le funiculaire est incomplet, le segment permettant de fermer le funiculaire — et donc de résoudre le problème — est appelé ligne de fermeture.

Dans l'analyse d'un problème, on peut souvent déterminer la direction d'une force inconnue, en fonction de la nature de la liaison avec son environnement ; par exemple, dans le cas d'un appui ponctuel sur un plan sans frottement, la force est perpendiculaire au plan. Si l'on ne connaît ni l'intensité ni la direction d'une force, il peut être intéressant de tracer le funiculaire à partir du point d'application de cette force, puisque c'est le seul point de la ligne d'action connu.

Lorsqu'un objet n'est pas en équilibre, la méthode permet de déterminer la résultante des forces s'exerçant sur l'objet (puisque c'est l'opposé de la force unique qui mettrait le solide en équilibre). Dans ce cas-là, les polygones ne sont pas fermés (puisque l'on n'est pas à l'équilibre) ; les extrémités du dynamique donnent le vecteur de la force résultante, et un point de la ligne d'action de la force résultante est donné sur le funiculaire par l'intersection des droites extrêmes.

On peut utiliser la méthode pour trouver le centre de gravité d'un système. En effet, le centre de gravité est l'endroit où on peut appliquer une force mettant le solide en équilibre si celui-ci n'est soumis qu'à son poids. Si le solide est composé de plusieurs parties dont on connaît les centres de gravité et les masses, il suffit de tracer le funiculaire en considérant les poids des différentes parties, et ce pour deux orientations différentes de l'objet ; l'intersection des lignes d'action des résultantes donne la position du centre de gravité. Par simplicité, on fait tourner le funiculaire et le dynamique plutôt que l'objet, et on considère deux directions perpendiculaire (l'horizontale et la verticale).

Étude de la flexion d'un ballon de reflux sous l'effet du poids : modélisation

Utilisation du funiculaire pour déterminer le diagramme des moments fléchissants ; la charge répartie q est remplacée par des charges ponctuelles, le polygone ainsi formé donne une approximation de la courbe

Utilisation du funiculaire pour déterminer la déformée : les moments fléchissants sont considérés comme une charge répartie, le funiculaire donne la déformée, si l'on choisit bien la position du pôle

Comparaison des résultats obtenus graphiquement (en cyan) avec la méthode des éléments finis (en rouge).

Le funiculaire est un moyen de faire une intégration graphique. On peut ainsi déterminer le diagramme des moments fléchissants ainsi que la déformée ; la détermination graphique de la déformée est appelée méthode de Mohr.

Le dynamique étant fait, on déplace le pôle pour que la ligne joignant les forces extrêmes soit horizontale. Le coefficient directeur des droites polaires est ainsi proportionnel aux intensités des forces cumulées. Le funiculaire que l'on trace présente des segments de droite y = ƒ(x ) où y est proportionnel à l'intensité de la force (pente de la droite) et à l'éloignement x, y représente donc un moment. Le funiculaire forme en fait le diagramme des moments fléchissants M_f, à l'échelle près. Cette échelle est déterminée par l'échelle des longueurs a (1 mm sur le dessin représente a mm réels soit 1:a), l'échelle des forces b (1 mm sur le dessin représente b N soit b N/mm) et la distance polaire p (distance du point P à la droite des forces) : 1 mm sur le diagramme des moments fléchissants représente abp Nmm.

Si l'on place le pôle à droite, on est en convention des efforts à droite de la coupure.

Si l'on découpe le diagramme des moments fléchissants en bandes d'égale largeur, l'aire de ces bandes est une primitive de la fonction. En considérant que ces aires sont des poids, appelés « charges fictives », et en traçant le funiculaire, on fait une intégrale graphique double de la charge répartie, ce qui donne le profil de la déformée u(x ). À un facteur près, la largeur réelle H des trapèzes, l'aire est égale à l'ordonnée au milieu du segment. La charge fictive est en fait M_f/(EI_Gz), E étant le module de Young du matériau et I_Gz le moment quadratique de la section droite par rapport à l'axe de flexion z ; si h est la largeur des trapèzes, l'échelle des charges fictives est donc 1 mm pour ha²bp/(EI_Gz) mm^-1.

Le pôle doit être placé à gauche ; cela correspond au fait qu'il y a un signe moins dans l'équation de la déformée lorsque l'on est en convention des efforts à droite de la coupure (M_f = -EI_Gzu"), et un signe plus lorsque l'on est en convention des efforts à gauche de la coupure (M_f = EI_Gzu"). Si p’ est la distance polaire utilisée pour tracer la déformée, alors 1 mm sur la figure correspond à ha³bpp’/(EI_Gz) mm dans la réalité. Le choix de distances polaires p et p’ permet de simplifier le calcul de l'échelle.

Si la section droite varie, il faut alors tracer un diagramme des charges fictives M_f/(EI_Gz) prenant en compte les variations du moment quadratique avant de tracer le funiculaire.

La précision de la méthode dépend de la précision du tracé et du nombre de trapèzes utilisés pour découper les charges réparties et le diagramme des moments fléchissants. Pour un tracé précis, on réalise une épure au format A0. Les erreurs se cumulent, le tracé de la déformée est donc plus éloigné de la solution théorique que le diagramme des moments fléchissants.