Méthode de la fausse position
La méthode de la fausse position ou méthode regula falsi ou méthode des excédents et déficits est au départ une méthode arithmétique.
Plus récemment, on appelle ainsi en analyse numérique, un algorithme de recherche d'un zéro d'une fonction, qui combine les possibilités de la méthode de dichotomie et de la méthode de la sécante.
La méthode arithmétique originelle
De l'Antiquité au XVIIe siècle, son efficacité a longtemps permis de régler les problèmes linéaires sans recours à l'algèbre. Il en existe deux versions : simple et double, qui établissent la solution cherchée en exploitant le défaut présenté par une (resp. 2) solution(s) supposée(s).
On trouve cette méthode notamment chez Fibonacci, Luca Pacioli, Nicolas Chuquet, Robert Recorde et antérieurement, en Chine, dans Les Neuf Chapitres sur l'art mathématique.
Fausse position simple
Elle règle les problèmes linéaires à une inconnue. Pour cela, on part d'une solution supposée et on évalue son résultat. En supposant la proportionnalité, une règle de trois donne la vraie solution.
Employée sinon explicitée en Égypte[1] , à Babylone[2] et dans l'Antiquité grecque tardive, on la trouve ensuite en Inde[3] et dans le monde arabe, puis en Occident.
Exemple
Les personnes A, B et C se sont partagé une certaine somme. A a reçu un tiers, B un quart, et C 1 760 écus. Quelle était la somme ?
- Résolution par fausse position
Si la somme à partager était de 12 écus - le choix de 12 est arbitraire, l'intérêt de ce nombre est que l'on peut en prendre facilement le quart et le tiers - la personne A aurait reçu le tiers de 12 écus soit 4 écus, la personne B aurait reçu le quart de 12 écus soit 3 écus et la personne C aurait reçu le reste soit 12 - 4 - 3 = 5 écus. Or il en a reçu 1 760. En appliquant une règle de trois sur 12, il est possible de trouver la somme à partager pour que la personne C recoive, non pas 5 écus, mais 1 760.
- La somme à partager est donc de écus;
- La personne A en reçoit le tiers soit 1 408;
- La personne B en reçoit le quart, soit 1 056;
- La personne C reçoit le reste soit 4 224 - 1 408 - 1 056 = 1 760.
- Résolution moderne
Si l'on appelle S la somme totale, et A, B, et C les parts respectives des personnes A, B et C on a :
- A = S/3, B = S/4, C = 1 760
et l'on sait que :
- A + B + C = S
ce qui donne l'équation :
- S/3 + S/4 + 1 760 = S
qui est bien une équation linéaire en S, puisqu'elle s'écrit :
- -5S/12 + 1 760 = 0
La méthode de la fausse position permet d'éviter l'étape de la mise en équation, mais ne fonctionne que pour un problème faisant intervenir une loi proportionnelle : ici la part de C est proportionnelle à la somme à partager.
Méthode
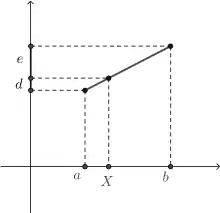
Elle règle les problèmes linéaires à deux inconnues. Pour cela, on part de deux solutions supposées, distinctes, dont on compare les écarts à l'objectif. La confrontation des excédents ou déficits mène à la solution comme somme pondérée d'écart nul des 2 solutions supposées.
Dans l'algorithme chinois[4], si la solution a conduit à un déficit d, et si la solution b conduit à un excédent de e, la bonne solution est .
La méthode se généralise à tout écart algébrique : si la première valeur x1 conduit à un écart δ1 et la seconde valeur x2 conduit à un écart δ2 alors la valeur permettant d'atteindre la cible est .
Cette propriété se démontre aisément en remarquant que, dans toute fonction affine, les écarts entre les images sont proportionnels aux écarts entre les antécédents. Ce qui donne:
Les plus anciens documents retrouvés relatifs à cette méthode remontent à une date estimée entre 200 av. J.-C. et 100, comme le texte chinois intitulé Les Neuf Chapitres sur l'art mathématique (Jiǔzhāng Suànshù)[5] et celui intitulé Livre sur les nombres et le calcul (Suàn shù shū)[6]. La méthode y est explicite et la démonstration utilise un principe analogue à la réduction au même dénominateur, une sorte d'homogénéisation des excédent-déficit[7]. Si la valeur a conduit à un déficit de d par rapport à la valeur pour X, la valeur ae conduit à un déficit de de par rapport à la valeur pour eX. Pour les mêmes raisons, la valeur bd conduit a un excédent de de par rapport à la valeur pour dX. Donc la valeur pour ae+bd est identique à celle pour eX+dX - car le déficit et l'excédent se compensent - et la valeur pour correspond à la valeur pour X. L'analogie avec la réduction au même dénominateur est tellement prégnante que, dans la procédure, a et b sont appelés les dividendes tandis que d et e sont appelés les diviseurs[6]. Longtemps utilisée seulement en Chine, cette méthode l'a ensuite été dans le monde arabe[8] puis en Occident.
Sur une cotisation commune
Cet exemple est tiré des Neuf Chapitres sur l'art mathématique[9] :
- Pour un achat en commun, si chacun paie 8, il y a 3 d'excédent et, si chacun paie 7, il y a 4 de déficit. Combien chacun doit-il payer ? Quel est le nombre de participants ? Quel est le montant de l'achat ?
Il s'agit d'un problème linéaire, la pente est le nombre de personnes, les x sont les quotas de chacun et les y la somme fournie.
- Résolution par fausse position
Le problème posé indique déjà les deux fausses positions : pour b=8, l'excédent est e=3 et pour a=7, le déficit est d=4
- la cotisation de chacun doit être de
- le nombre de cotisants (coefficient de colinéarité) est
- le montant de l'achat est
- Résolution moderne
Les inconnues sont : N pour le nombre de participants et S pour le montant de l'achat. Les données conduisent au système d'équations
Sur un système de deux équations à deux inconnues
Ce marchand a acheté 120 foulards, les uns à 2 écus, les autres à 5 écus, pour une somme de 468 écus. Combien a-t-il acheté de foulards de chaque sorte ?
- Résolution par fausse position
Les fausses positions vont porter sur le nombre de foulards à 2 écus.
- Si l'on achète 60 foulards à 2 écus : on achète alors 120 - 60 = 60 foulards à 5 écus et le montant de l'achat aurait été de 60×2 + 60×5 = 420 écus, d'où un déficit de 468 - 420 = 48 écus.
- Si l'on achète 50 foulards à 2 écus : on achète 120 - 50 = 70 foulards à 5 écus et le montant de l'achat aurait été auraient été 50×2 + 70×5 = 450 écus, d'où un déficit de 468 - 450 = 18 écus.
Ici, il s'agit de deux déficits, il faut prendre la formule généralisée : le nombre exact de foulards à 2 écus est donc de . Il a donc acheté 44 foulards à 2 écus (soit 88 écus) et 120 - 44 = 76 foulards à 5 écus (soit 380 écus).
- Résolution moderne
La méthode permet de résoudre un système de deux équations linéaires à deux inconnues. En effet, si l'on appelle n2 le nombre de foulards à 2 écus et n5 le nombre de foulards à 5 écus, alors le problème se traduit par :
Interpolation linéaire dans un problème non linéaire
Cet exemple est tiré du Livre sur les nombres et le calcul (Suàn shù shū)[10]
Soit un champ d'un mǔ (en métrologie chinoise, un mǔ correspond à 240 bù-carré, soit environ 600 m²) : de combien de bù est-il carré ?
Ce problème n'est pas un problème linéaire, mais on peut approcher localement la parabole correspondante par un segment de droite
- Résolution par fausse position
- Si le côté est de 15 bù, l'aire est de 225 bù² soit un déficit de 240 - 225 = 15
- Si le côté est de 16 bù, l'aire est de 256 bù² soit un excédent de 256 - 240 = 16
Le processus par excédent et déficit donne un carré de côté bù.
- Résolution par extraction de racine carrée
On trouve ce système d'interpolation linéaire également dans trois problèmes (11-18-20) du chapitre VII sur excédent et déficit dans Les Neuf Chapitres sur l'art mathématique (Jiǔzhāng Suànshù)[11] sans que ne soit clair dans le texte qu'il ne s'agisse que d'une approximation. Cette utilisation préfigure, sans son itération, la méthode de fausse position développée en analyse.
La méthode de fausse position en analyse numérique
C'est une méthode itérative pour trouver un zéro d'une fonction continue, méthode dont chaque étape relève de la fausse position double originelle.
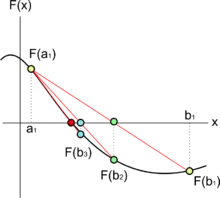
Recherche du zéro de la sécante
Étant donnés a et b, on construit la droite passant par les points (a, f(a)) et (b, f(b)), comme dans la figure ci-contre.Cette droite est une sécante ou une corde du graphe de la fonction f. En utilisant la pente et un point, l’équation de la droite peut s’écrire :
On détermine maintenant c, l’abscisse du point d’intersection de cette droite avec l’axe des abscisses (zéro de la sécante) donnée par :
La résolution de l’équation précédente donne c :
Déroulement du calcul
Comme la méthode de dichotomie, la méthode de la fausse position commence par deux points a1 et b1 tels que f(a1) et f(b1) soient de signes opposés, ce qui implique d’après le théorème des valeurs intermédiaires que la fonction continue f possède au moins un zéro dans l’intervalle [a1, b1]. La méthode consiste à produire une suite décroissante d’intervalles [ak, bk] qui contiennent tous un zéro de f. À l’étape k, le nombre :
est calculé. Comme expliqué ci-dessus, ck est l’abscisse de l’intersection de la droite passant par (ak, f(ak)) et (bk, f(bk)) avec l'axe des abscisses, appelée pour simplifier zéro de la sécante. Si f(ak) et f(ck) sont de même signe, alors on pose ak+1 = ck et bk+1 = bk, sinon ak+1 = ak et bk+1 = ck. Ce procédé est répété jusqu’à ce que le zéro soit suffisamment approché, c'est-à-dire que l'écart entre ck+1 et ck soit inférieur à un écart ε acceptable.
La formule ci-dessus est également employée dans la méthode de la sécante, mais cette dernière retient systématiquement les deux derniers points calculés, alors que la méthode de la fausse position retient deux points qui encadrent certainement un zéro. D'autre part, la seule différence entre la méthode de la fausse position et la méthode de dichotomie est l’utilisation dans cette dernière de la relation ck = (ak + bk) / 2.
Analyse
Si les valeurs initiales a0 et b0 sont prises telles que f(a0) et f(b0) soient de signes opposés, alors la méthode de fausse position convergera vers un zéro de f. La vitesse de convergence sera typiquement superlinéaire, ainsi plus rapide que la méthode de dichotomie, mais plus lente que la méthode de Newton. Il faut toutefois rappeler que la méthode de Newton peut diverger, tout comme la méthode des sécantes.
Note et référence
- Jérôme Gavin et Alain Schärlig 2015, p. 113.
- Jérôme Gavin et Alain Schärlig 2012, p. 37-40.
- Jérôme Gavin et Alain Schärlig 2012, p. 51-52.
- Chemla 1988, p. 67-68.
- Chemla 1988, p. 63.
- C. Cullen 2004, p. 81.
- Chemla 1988, p. 72-74.
- C. Cullen 2004, p. 63-64.
- Chemla 1988, p. 66.
- C. Cullen 2004, p. 88.
- Karine Chemla et Guo Shuchun, Les neuf chapitres : Le classique mathématique de la Chine ancienne et ses commentaires [détail de l’édition], pp 553; 577; 589-593;597
Voir aussi
Article connexe
Bibliographie
- (en) Steven C. Chapra et Raymond P. Canale, Numerical methods for Engineers, McGraw-Hill, , 6e éd. (ISBN 978-0-07-126759-5)
- (en) Richard L. Burden et J. Douglas Faires, Numerical Analysis, Brooks/Cole, , 9e éd. (ISBN 978-0-538-73351-9)
- Jérôme Gavin et Alain Schärlig, Longtemps avant l'algèbre : La Fausse Position, ou comment on a posé le faux pour connaître le vrai..., Lausanne, Presses Polytechniques et Universitaires Romandes, , 222 p. (présentation en ligne)
- Jérôme Gavin et Alain Schärlig, « Fausse position et heuristique au Moyen Empire », ENiM, no 8, , p. 113-132 (lire en ligne)
- C. Cullen, The Suàn shù shū (Writings on reckoning) : A translation ofa Chinese mathematical collection of thesecond century BC, with explanatory commentary, Needham Research Institute Working Papers, (lire en ligne), p. 81-88
- Karine Chemla, « La pertinence du concept de classification pour l'analyse de textes chinois », Extrême-Orient, Extrême-Occident, no 10, , p. 61-87
Liens externes
- Alaeddine Ben Rhouma, « Master : Autour de la proportionnalité », INSMI, sur HAL,
- Serge Mehl, « Méthodes de fausse position », sur ChronoMath
- De la « fausse position » aux timides débuts de l’algèbre, article (2014) de J. Gavin et A. Schärlig sur le site BibNum.
- Jérôme Gavin et Alain Schärlig, « La regula falsi », sur Images des maths,
- Portail de l'analyse
- Portail de l'informatique théorique