Méthode mathématique d'analyse multicritère
Les méthodes mathématiques d'analyse multicritère ont pour but la résolution des problèmes d'Aide à la décision multicritère[1]. Elles constituent une étape importante du processus de décision, qui suit celle d'identification et de définition du problème, et aboutissent au choix d'une ou plusieurs solutions optimale(s), au sens de Pareto, parmi un ensemble discret de solutions, via une procédure de sélection. Elles permettent également de répondre aux problématiques de tri et de rangement, par l'intermédiaire d'une procédure d'affectation et de classement respectivement.
Ces méthodes sont issues principalement des travaux de Thomas L. Saaty et du chercheur Bernard Roy, créateur du LAMSADE (Laboratoire d'analyse et modélisation de systèmes pour l'aide à la décision).
Elles sont confrontées à deux limites : l'une liée au manque de données fiables sur une durée suffisante, ce qui peut empêcher la construction ou la validation de la méthode ; l'autre liée à la technicité inhérente à de telles méthodes puisque ces dernières nécessitent l'usage de concepts délicats qui peuvent déboucher sur des résultats erronés ou une analyse confuse. Ces méthodes héritent également des problèmes informatiques, notamment celui de l'explosion combinatoire.
Il existe de nombreuses méthodes mathématiques d'analyse multicritère, mais celles-ci peuvent être regroupées en deux approches[2] :
- agrégation a priori de critères en un critère unique ;
- approche fondée sur le surclassement[3].
Définitions
Action
L'Aide à la décision multicritère s'intéresse au choix parmi un nombre fini d'actions possibles (projet, investissement, décision, solution, plan, variante, candidat...) pour atteindre un objectif.
Critère
Un critère est une fonction définie sur l'ensemble des actions représentant les préférences de l'utilisateur selon son point de vue.
Poids
Le poids mesure l'importance d'un critère par rapport aux autres du point de vue du décideur[4].
Agrégation a priori de critères en un critère unique
Somme pondérée
La méthode de la somme pondérée est connue de par son accessibilité mathématique.
Formulation mathématique
Données de départ
- m actions A1, A2, A3...Am
- n critères C1, C2, C3...Cn
- Vecteur poids (W1, W2,...Wn) et Wj > 0
- aij = Uj(Ai), fonction d'utilité cardinale quotient, c'est-à-dire que cette fonction représente les écarts en plus de respecter l'ordre et pour laquelle il existe un zéro véritable. Ces données représentent les performances de chaque action sur chacun des critères.
Transformation des données
- Normalisation de tous les aij afin de conserver la proportionnalité entre les valeurs.
- Normalisation des poids (la somme des poids = 1).
- Mise en œuvre de la méthode Somme pondérée.
- Donc un critère unique pour toute action i
Exemple d'utilisation de cette méthode
On propose d'appliquer cette méthode au choix de sélection d'une ville ou d'un territoire en fonction de son attractivité à développer les déplacements doux et/ou ayant adopté une démarche de développement durable et notamment avec la réduction des gaz à effet de serre. Il s'agit de trouver la ville ou les villes qui sont les plus attractives sur les 5 villes, puis de les classer de la plus pertinente à la moins pertinente.
Objet de la décision : Mobilité responsable et développement d'infrastructures pour le développement durable
On considère les six critères suivants :
- Attractivité climatique : C1 : Si un territoire présente un climat doux avec une pluviométrie acceptable, il favorise les déplacements pédestres et des transports doux (vélo,...). Il est évalué à partir de la température moyenne annuelle, du nombre d'heures d'ensoleillement et de la hauteur des précipitations. Ce critère est à maximiser.
- Accessibilité piéton/vélo : C2 : Si les différents secteurs de la ville sont accessibles facilement à pied ou à vélo ; si le relief est faiblement pentu : il favorise l'usage de la marche ou la bicyclette. Son indicateur est le % de marche utilisé + % d'usage du vélo. Ce critère est à maximiser.
- Transports en commun : C3 : L'usage des transports en commun est lié à la politique locale de l'agglomération qui a favorisé son développement : il s'agit en fait d'un indicateur de l'adhésion des populations à ces transports. Ce critère est à maximiser.
- Automobile : C4 : L'usage des véhicules personnels est un indicateur de la ville concernant d'une part son accessibilité, et du comportement urbain des habitants lié à différents facteurs : il est caractérisé par le % d'usage de la voiture dans la mobilité. Ce critère est à minimiser.
- Mobilité : C5 : Nombre de déplacement par jour et par habitant. Il exprime soit une nécessité ou un intérêt à se déplacer pour les habitants du territoire. Ce critère est à minimiser.
- Profil de la population : C6 : L'indicateur donné est le pourcentage de la population ayant plus de 60 ans. Ce critère est à maximiser.
Les valeurs des poids sont données dans le tableau ci-dessous (choix du décideur) :
Critère Description Poids 1 Attractivité climatique 16 2 Accessibilité piéton/vélo 18 3 Transports en commun 18 4 Automobile 18 5 Mobilité 24 6 Profil de la population 6
Voici la matrice des décisions (tableau des performances) :
N° Ville Attractivité climatique Accessibilité piéton/vélo Transports en commun Automobile Mobilité profil de la population 1 3 32 11 42 3,54 21,85 2 2 32 14 41 3,63 18,6 3 2 31 7 45 3,99 12,9 4 2 32 6 43 3,75 27,3 5 2 25 10 49 3,52 16,5
Afin d'avoir une somme pondérée cohérente, il est nécessaire de ne considérer que des critères à maximiser. Toutefois, les critères Automobile et Mobilité sont à minimiser. Une transformation de ces données s'impose alors afin d'obtenir deux critères à maximiser. La transformation adéquate est la suivante :
Cette transformation maintient les écarts et permet de conserver un zéro véritable, et échange l'ordre afin de considérer alors un critère à maximiser. On les notera C4' et C5'.
Voici la matrice des décisions sur laquelle la méthode Somme pondérée peut alors s'appliquer :
N° Ville Attractivité climatique Accessibilité piéton/vélo Transports en commun Automobile C4' Mobilité C5' Profil de la population 1 3 32 11 7 0,45 21,85 2 2 32 14 8 0,36 18,6 3 2 31 7 4 0 12,9 4 2 32 6 6 0,24 27,3 5 2 25 10 0 0,47 16,5
On applique alors la méthode des Sommes pondérées et on choisit comme procédure de normalisation :
- Normalisation des aij
Considérons l'exemple de la première ligne :
N° Ville Attractivité climatique Accessibilité piéton/vélo Transports en commun Automobile C4' Mobilité C5' Profil de la population Somme de la ligne 1 3 32 11 7 0,45 21,85 75,3
On réalise alors l'opération suivante : . Voici le critère la première ligne normalisée :
N° Ville Attractivité climatique Accessibilité piéton/vélo Transports en commun Automobile C4' Mobilité C5' Profil de la population 1 0,0397 0,4238 0,1457 0,0927 0,0086 0,2894
- Normalisation des poids
Critère Description Poids 1 Attractivité climatique w1 = 0,16 2 Accessibilité piéton/vélo w2 = 0,18 3 Transports en commun w3 = 0,18 4 Automobile w4 = 0,18 5 Mobilité w5 = 0,24 6 Profil de la population w6 = 0,06
- Somme pondérée
On effectue finalement l'opération suivante
Par exemple, pour la ligne 1, on effectue cette opération :
On effectue alors cette opération pour chacune des lignes.
Interprétation de la méthode de la somme pondérée
Une fois ce travail réalisé, l'interprétation des résultats s'impose. On trie alors les sommes pondérées résultantes dans l'ordre décroissant, ce qui permet la réalisation d'un classement des villes.
Voici les trois premières villes du classement :
Préférence N° Ville Somme pondérée 1 Ville n° 3 0,1524 2 Ville n° 2 0,1502 3 Ville n°1 0,1450
Attention : Le classement obtenu dépend de la procédure de normalisation.
Le décideur peut alors soit se fier à cette analyse et choisir la ville n°3, soit demander que soient mises en œuvre d'autres méthodes de Somme pondérée avec d'autres procédures de normalisation et obtenir ainsi une position moyenne des différentes villes et choisir celle qui a la meilleure position moyenne.
Il est important de noter que la pondération a été fournie par le décideur et que celle-ci répond à ses préférences personnelles. D'autres pondérations donneraient des résultats tout à fait différents.
Limites et désavantages de cette méthode
La méthode de la somme pondérée possède deux avantages principaux :
- Il s'agit d'un modèle simple
- La solution optimale d'une somme pondérée est efficace
Cependant de nombreuses limites existent vis-à-vis de cette méthode, notamment due à l'interprétation des poids qui prennent en compte[5] :
- L'importance relative des critères
- Un facteur de normalisation des échelles des critères
La méthode de la somme pondérée nécessite donc d'avoir des critères comparables et d'intégrer l'influence de la normalisation préalable.
Analyse multicritères hiérarchique (AMCH)
Il s'agit de la méthode dont Thomas L. Saaty est l'inventeur, l'architecte et le premier théoricien (1980). Elle repose sur trois concepts :
- La structuration hiérarchique : décomposition du problème en sous problèmes.
- La structuration des priorités : classement des éléments selon leur importance relative.
- La cohérence logique : les éléments sont regroupés et classés de façon logique.
Cette méthode présente plusieurs intérêts notables et permet de :
- élaborer un compromis représentatif des divers avis mais pas nécessairement le consensus ;
- affiner la définition d'un problème par la décomposition ;
- établir des priorités ;
- prendre en compte l'interdépendance des éléments ;
- évaluer la cohérence logique des avis utilisés.
Formulation mathématique
Pour trouver la ou les solutions idéale(s) il faut appliquer au problème l'algorithme suivant :
- Construire la hiérarchie : Il faut déterminer les différents niveaux hiérarchiques et choisir les critères à chaque niveau. La comparaison s'effectue selon les critères de niveau équivalent. Par exemple à l'achat d'une voiture, l'utilisateur peut décomposer son objectif final "acheter la voiture la plus attrayante" en trois éléments comme les performances moteur, l'équipement et le prix. De plus ces critères peuvent être décomposés en sous-critères. Ainsi l'utilisateur peut décomposer le critère performances moteur en critères de niveau inférieur comme la consommation, l'accélération ou le couple.
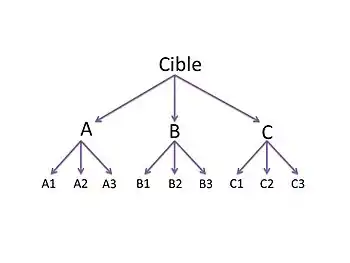 La structuration hiérarchique
La structuration hiérarchique - Établir le poids des critères et sous-critères : Le décideur définit les priorités en comparant de manière binaire les éléments de la hiérarchie. Pour chaque niveau du sommet à la base, il doit comparer les éléments deux à deux par rapport au critère supérieur. Par exemple, il doit se demander comment l'élément A1 satisfait-il mieux le critère A que l'élément A2. Pour formuler ses priorités il peut utiliser une échelle de comparaison binaire ci-dessous.
Appréciation Degré d'importance Importance égale de deux éléments 1 Faible importance d'un élément par rapport à un autre 3 Importance moyenne d'un élément par rapport à un autre 4 Importance forte d'un élément par rapport à un autre 5 Importance attestée d'un élément par rapport à un autre 7 Importance absolue d'un élément par rapport à un autre 9
- 3. Écrire les matrices de comparaison binaire pour chaque niveau: Cette matrice est la représentation du résultat de l'étape précédente. En voici un exemple :
| Critères | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 0.25 | 0.2 |
| A2 | 4 | 1 | 0.33 |
| A3 | 5 | 3 | 1 |
On compare l'élément de la colonne de gauche par rapport à celui de la ligne du haut. Ainsi A3 est 5 fois plus important que A1, A3 est 3 fois plus important que A2.
- 4. Déterminer les poids des critères : Pour réaliser cette étape, normaliser les colonnes de la matrice de comparaison. La somme des éléments de chaque colonne vaut 1. Ensuite sommer les éléments de chaque ligne. Le poids du critère nous est donné par la formule :
- 5. Évaluer la cohérence des jugements Nous pouvons évaluer la cohérence des poids des critères. Si nous choisissons A1 trois fois plus important que A2 lui-même deux fois plus important que A3 et que dans un même temps A3 cinq fois plus important que A1 alors les indicateurs indice de cohérence et ratio de cohérence nous avertiront que les solutions risquent d'être quelque peu aléatoires. Si le ratio de cohérence est inférieur ou égal à 10 %, l'appréciation est jugée cohérente.
- Pour obtenir la cohérence moyenne on multiplie chaque colonne de la matrice de comparaison binaire non normalisée par le poids du critère associé. On calcule alors pour chaque ligne la somme des éléments. La cohérence de chaque critère est donnée par la somme précédente divisée par le poids du critère de la ligne. En sommant la cohérence de chaque critère et en divisant par le nombre des critères, on obtient la cohérence moyenne.
La cohérence aléatoire est donnée par le tableau suivant :
| Nombre de critères | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| Cohérence aléatoire | 0.00 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
- Si les ratios de cohérence sont bons alors on peut passer à l'étape suivante, sinon il est préférable de recommencer la comparaison binaire.
- 6. Évaluer les poids de chaque critère par rapport au critère supérieur On pondère le poids des sous-critères par le poids des critères supérieurs. Mathématiquement, pour tous les sous-critères, on calcule le poids du couple A1/A comme le poids du sous-critère A1 multiplié par le poids du critère supérieur A. Nous disposons donc d'un poids pondéré pour chaque sous-critère.
- 7. Sélectionner uniquement les sous-critères de poids pondérés préférentiels Pour chaque critère, il ne faut retenir qu'un seul sous-critère. Il faut donc choisir ceux dont leur poids pondéré est le meilleur vis-à-vis des autres sous-critères. Il reste ensuite à normaliser les poids pondérés des critères choisis.
- 8. Évaluer les actions/projets Il s'agit d'établir le poids des projets par rapport aux sous-critères. Pour tous les critères préférés sélectionnés à l'étape 6, écrire une matrice de comparaison. Effectuer les calculs des étapes 3, 4 et 5 pour toutes ces matrices et évaluer les indices de cohérence ainsi que les poids pour chaque action.
Pour A1/A Projet1 Projet2 Projet3 Poids de l'action pour le sous-critère A1/A Projet1 1 2 3.33 0.551 Projet2 0.5 1 2 0.293 Projet3 0.3 0.5 1 0.156
- 9. Décider de l'action à choisir Pour chaque action calculer :
- À partir des sommes obtenues pour chaque action nous pouvons établir un classement préférentiel. Une action ayant une somme importante est une action à privilégier.
Exemple d'utilisation de cette méthode
La problématique de l'exemple traité avec la méthode Somme pondérée est reprise et la résolution se réalise désormais grâce à la méthode de Saaty. Les six critères qui étaient proposés ont été légèrement modifiés en huit sous-critères afin de pouvoir répondre à l'arborescence inhérente à cette méthode[6].
- 1. Construire la hiérarchie :
En voici une représentation graphique, sous forme d'arbre :
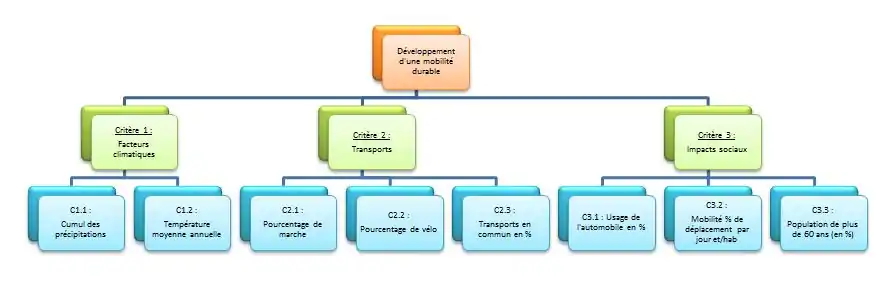
Ci-dessous la matrice des décisions avec comme objectif de trouver une ville pertinente. Comme expliquée dans la méthode Somme pondérée les critères à minimiser ont été modifiés de sorte que chaque critère ci-dessous soit à maximiser.
N° ville Cumul des précipitations C11 Température moyenne annuelle C12 Pourcentage de marche C2.1 Pourcentage de vélo C2.2 Transports en commun en % C2.3 Usage de l'automobile en % C3.1' Mobilité % de déplacement par jour et/hab. C3.2' population de plus de 60 ans (en %) C3.3 1 0,5 1 32 0 11 7 0,65 21,85 2 0 0,5 31 1 14 8 0,56 18,6 3 0 0 29 2 7 4 0,2 12,9 4 0 0,5 31 1 6 6 0,44 27,3 5 0,5 0,5 22 3 10 0 0,67 16,5
- 2. Établir le poids des critères et sous-critères : Dans cet exemple nous avons supposé que les transports ont une importance forte comparés aux facteurs climatiques pour répondre à une problématique de développement de mobilité durable. C2 vaut donc 7 fois C1. On compare ainsi tous les critères entre eux et tous les sous critères entre eux.
- 3. Écrire les matrices de comparaison binaire pour chaque niveau:
Critères C1 C2 C3 C1 1 0,1429 0,25 C2 7 1 4 C3 4 0,25 1 Somme 12 1,3929 5,25
Afin de normaliser, on calcule la somme de chaque colonne. On normalise les éléments en les divisant par la somme de leur colonne. On obtient la matrice de comparaison normalisée.
Critères C1 C2 C3 Somme ligne C1 1/12= 0,0833 0,1026 0,0476 0,2335 C2 0,5833 0,7179 0,7619 2,0632 C3 0,3333 0,1795 0,1905 0,7033
- 4. Déterminer les poids des critères : En divisant la somme des éléments d'une ligne par le nombre de critères on obtient le poids de chaque critère.
Critères Poids des critères C1 0.2335/3= 0,0778 C2 0,6877 C3 0,2344
- 5. Évaluer la cohérence des jugements : On multiplie chaque colonne de la matrice de comparaison non normalisée par le poids du critère associé.
Critères C1 C2 C3 Somme ligne C1 1*0,0778= 0,0778 0,09821 0,0586 0,2346 C2 7*0,0778= 0,5448 0,6877 0,9377 2,1702 C3 0,3113 0,17193 0,2344 0,7177
On évalue ensuite la cohérence en divisant la somme des lignes obtenue par le poids du critère de la ligne :
Critères Cohérence C1 0,2346/0,0778= 3,0151 C2 3,1558 C3 3,0615 Cohérence moyenne 3,0775
En appliquant les formules mathématiques on détermine les ratios de cohérences.
Indice de cohérence : 0,0387
Ratio de cohérence : 0,0668 < 0.1 donc la matrice de comparaison choisie arbitrairement est sensée.
Il faut effectuer toutes ces opérations pour l'ensemble des sous-critères. Si l'ensemble des jugements de cohérence sont corrects, on peut passer à l'étape suivante.
- 6. Évaluer les poids de chaque critère par rapport au critère supérieur :
Voici les résultats obtenus pour les sous-critères de C2. Ils ont été obtenus de manière analogue aux critères.
Critère C2 C2.1 C2.2 C2.3 Poids des sous-critères C2.1 1 0,3333 0,1667 0,0915 C2.2 3 1 0,2 0,2014 C2.3 6 5 1 0,7071 Somme 10 6,3333 1,3667
- 7. Sélectionner que les sous-critères de poids pondérés préférentiels :
Pour chaque sous-critère on calcule le poids du sous critère * le poids du critère supérieur. Pour chaque critère on sélectionne le sous-critère ayant obtenu la meilleure valeur. Dans notre cas, pour le critère C2 le sous-critère C2.3 s'avère le meilleur. C'est donc sur lui que nous allons travailler. Nous sélectionnons aussi C1.2 et C3.2.
C1.2 0,0519 C2.3 0,7071*0,6877= 0,4863 C3.2 0,1381 Somme 0,6762
Nous normalisons ensuite les poids pondérés :
C1.2/C1 0,0767 C2.3/C2 0,7191 C3.2/C3 0,2042
- 8. Évaluer les actions/projets :
Nous nous plaçons pour évaluer la matrice de comparaison pour le sous-critère pondéré C2.3/C2. Nous calculons donc les rapports entre les différentes villes pour le critère C2.3. Cette étape est à faire pour tous les sous-critères sélectionnés.
C2.3/C2 1 2 3 4 5 1 1 0,7857 1,5714 1,8333 1,1 2 14/11= 1,2727 1 2 2,3333 1,4 3 7/11= 0,6364 0,5 1 1,1667 0,7 4 0,5455 0,4286 0,8571 1 0,6 5 0,9091 0,7143 1,4286 1,6667 1 Somme 4,3636 3,4286 6,8571 8 4,8
Nous calculons ensuite les poids de chaque action. La méthode est identique à celle du début : somme des colonnes, normalisation du tableau précédent puis somme des lignes et division par le nombre de critères.
Ville Poids de la ville pour C2.3/C2 1 0,0572 2 0,0729 3 0,0364 4 0,0312 5 0,0520
- 9. Décider de l'action à choisir :
Nous appliquons la formule suivante :
C1,2/C1 C2.3/C2 C3,2/C3 Somme ligne 1 0,0066 0.0572*0.7191= 0,0412 0,0098 0,0576 2 0,0049 0,0524 0,0101 0,0674 3 0,0014 0,0262 0,0110 0,0387 4 0,0043 0,0225 0,0104 0,0371 5 0,0020 0,0375 0,0097 0,0492
Il ne reste plus qu'à interpréter la somme des lignes.
Interprétation de la méthode AMCH
À l'instar de la méthode Somme pondérée, le tableau des préférences est obtenu.
Ci-dessous le tableau susnommé :
Préférences N° des villes Evaluation finale 1 Ville n°2 0,0674 2 Ville n°1 0,0576 3 Ville n°5 0,0492
Le classement est différent de celui que fournit la méthode la Somme pondérée ; ceci s'explique par les différences notables entre les deux méthodes, notamment quant à l'utilisation d'une matrice de comparaison binaire / critère.
D'après cette méthode, la ville la plus attractive est la ville n°2. Cette dernière arrivant deuxième dans l'ordre de préférence pour la méthode de la Somme pondérée, elle constitue un choix logique pour le décideur.
Limites et désavantages de cette méthode
D'après Bernard Roy, les principaux avantages de la méthode de Saaty sont :
- la représentation et décomposition hiérarchique d'un problème complexe en éléments séparés
- le tri des éléments d'un système en différents niveaux selon leur importance relative
- le regroupement de ces éléments de façon logique et leur classement de façon cohérente selon des critères logiques
Toutefois, celle-ci présente tout de même quelques limites[5] :
- elle peut être délicate à mettre en œuvre dans une problématique multi-acteurs ou lorsque les critères sont trop nombreux, le risque d'incohérence des jugements étant alors trop élevé.
- cette méthode demande au décideur de considérer toutes les comparaisons possibles, faisant implicitement l’hypothèse que tous les critères considérés sont parfaitement comparables
Approche fondée sur le surclassement
C'est dans ce cadre que s'insère la méthode ELECTRE. ELECTRE est une famille de méthodes mathématiques d'analyse multicritère, développée par Bernard Roy à partir des années 1960[3].. L'acronyme ELECTRE signifie ELimination Et Choix Traduisant la REalité.
Cette méthode repose sur l'utilisation d'un graphe orienté pour représenter les relations entre les différentes actions.
Définitions pratiques
- Relation de préférence entre 2 actions
Relation notée P : si a est préférée à b
- Relation d'indifférence
Relation notée I : indifférence entre 2 actions :
- Relation d'incomparabilité
Relation notée R : 2 actions incomparables :
Cela équivaut à :
- Relation de surclassement
Une relation de surclassement, appelée aussi relation de préférence au sens large, est la réunion d'une relation de préférence au sens strict (la relation P) et d'une relation d'indifférence (relation I).
signifie a surclasse b.

- Le noyau du graphe
Il est noté N et est composé de sommets tels que :
- tous les sommets qui n'appartiennent pas au noyau sont surclassés par un sommet du noyau au moins
- les sommets du noyau ne se surclassent pas entre eux
- Indice de concordance (d'après Maystre et al.94)
"Il est dit du critère j qu'il concorde avec l'hypothèse "l'action ai surclasse l'action ak " si l'action ai est au moins aussi bonne que l'action ak en ce qui concerne le critère j ; ce qui se traduit par :"
- Indice de non-discordance
" La condition de non-discordance permet de refuser le surclassement d'une action sur une autre, obtenue après application de la condition de concordance, lorsqu'il existe une opposition trop forte sur un critère au moins "
Le déroulement de la méthode
Sur l'ensemble des actions possibles, on cherche au moyen d'une relation de surclassement S au préalable définie, une partition de l'ensemble des actions possibles entre le noyau N et son complémentaire.
- 1. Affectation des poids Pj à chaque critère : L'utilisateur défini ses préférences.
- 2. Recalibration : L'utilisateur doit recalibrer les valeurs des différentes actions en fonction des critères sur une plage de donnée. Par exemple la valeur d'une action associée à un critère doit appartenir à une échelle de note de 0 à 20. On obtient alors une nouvelle matrice actions/critères.
- 3. Établir les relations entre les actions : L'utilisateur définit ses préférences. On écrit une matrice dite de comparaison entre actions pour chaque critère. On compare l'action de la ligne i avec celle de la colonne j. Par exemple, à la ligne 2 et première colonne de notre matrice, on va comparer le projet 2 au projet 1 pour le critère i :
- Si la valeur du projet 2 est supérieure à celle du projet 1 ; on remplit la case du caractère J+.
- Si la valeur du projet 2 est inférieure à celle du projet 1 ; on remplit la case du caractère J-.
- Si la valeur du projet 2 est égale à celle du projet 1 ; on remplit la case du caractère J=.
On effectue cette opération pour tous les éléments à comparer et pour tous les critères.
- 4. Définir les ensembles J+, J−, J= : On écrit une matrice dite " ensemble des J+ ". Dans cette matrice on récapitule les préférences entre les actions pour tous les critères. Pour à la ligne i et à la colonne j si l'action i est préférée à l'action j pour les critères 2 et 3 alors on écrit dans cette matrice l'ensemble {2,3} à la i et à la colonne j. De même on tabule les tableaux :" ensemble des J− "et " ensemble des J= ".
- 5. Définir l'ensemble de concordance : Il faut juste écrire la matrice J+ U J=
- 6. Calcul des coefficients de concordances entre les actions : On effectue cette opération à partir du tableau précédent. A la ligne i et à la colonne j, on somme les poids des critères sélectionnés. Si l'on avait {2,3} dans l'ensemble de concordance, on aura Poids(C2)+Poids(C3) dans notre nouvelle matrice.
- 7. Calcul des coefficients de discordances Dik entre les actions : Les ai représentent les actions,
gj(ai) représente la valeur de l'action i pour le critère j. Pour remplir la matrice suivante il faut suivre la méthode suivante pour la ligne i et la colonne k
- 8. Filtrer les actions : Placer sur un graphe les différentes actions.Fixer un seuil un seuil, par exemple 0.250. Pour toutes les lignes i et colonnes j si les coefficients de concordances sont supérieurs à 0.75 et si les coefficients de discordances sont inférieurs à 0.25. alors on peut tracer un arc de l'action i vers j.
- 9. Déterminer le noyau : À partir du graphe précédent, nous pouvons trouver le noyau et donc les actions à privilégier.
Exemple d'utilisation de cette méthode
On reprend la matrice des décisions de la méthode Somme pondérée. Nous considérons ainsi cinq villes selon six critères, ainsi que les poids qui y sont définis.
- 2. Recalibration :
Voici la matrice des décisions "recalibrée" sur une échelle de 0 à 10;
N° ville attractivité climatique C1" Vélo + pieton en % C2" Transports en commun en % C3" Usage de l'automobile en % C4" Mobilité % de déplacement par jour et/hab. C5" population de plus de 60 ans (en %) C6" 1 10 10 6,25 8,75 9,5745 6,2153 2 0 10 10 10 7,6596 3,9583 3 0 (31-25)*10/(32-25)= 8,5714 1,25 5 0 0 4 0 10 0 7,5 5,1064 10 5 0 0 5 0 10 2,4913
- 3. Établir les relations entre les actions :
Tableau de comparaison entre actions pour C1"
N° ville 1 2 3 4 5 1 J+ J+ J+ J+ 2 J- J= J= J= 3 J- J= J= J= 4 J- J= J= J= 5 J- J= J= J=
- 4. Définir les ensembles J+, J−, J= :
Ensemble des J-. On écrit aussi l'ensemble J+ et J=.
N° ville 1 2 3 4 5 1 {3,4} 0 {6} {5} 2 {1,5,6} 0 {6} {5} 3 {1,2,3,4,5,6} {2,3,4,5,6} {2,4,5,6} {3,5,6} 4 {1,3,4,5} {3,4,5} {3} {3,5} 5 {1,2,3,4,6} {2,3,4,6} {2,4} {2,4,6}
- 5. Définir l'ensemble de concordance :
Ensemble des
N° ville 1 2 3 4 5 1 {1,2,5,6} {1,2,3,4,5,6} {1,2,3,4,5} {1,2,3,4,6} 2 {2,3,4} {1,2,3,4,5,6} {1,2,3,4,5} {1,2,3,4,6} 3 0 {1} {1,3} {1,2,4} 4 {2,6} {1,2,6} {1,2,4,5,6} {1,2,4,6} 5 {5} {1,5} {1,3,5,6} {1,3,5}
- 6. Calcul des coefficients de concordances entre les actions :
N° ville 1 2 3 4 5 1 0,64 1 0,94 0,76 2 0.18+0.18+0.18 = 0,54 1 0,94 0,76 3 0 0,16 0,34 0,52 4 0,24 0,4 0,82 0,58 5 0,24 0,4 0,64 0,58
- 7. Calcul des coefficients de discordances Dik entre les actions :
N° ville 1 2 3 4 5 1 (10-6.25) / 10 = 0,375 0 0,3785 0,0426 2 1 0 0,6042 0,1467 3 1 0,875 1 1 4 1 1 0,125 0,5 5 1 1 0,8571 1
- 8. Filtrer les actions :
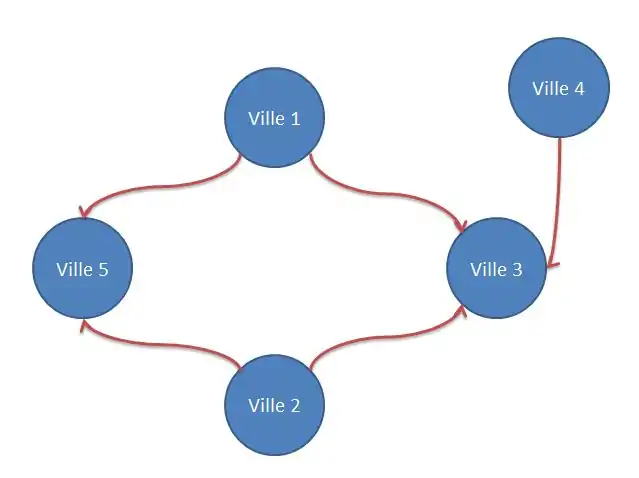
- 9. Déterminer le noyau :
Le noyau est constitué des villes 1, 2 et 4.
Interprétation de la méthode de la somme pondérée
Les différentes villes composant le noyau sont susceptibles d'être, chacune, la meilleure solution alors que les villes qui n'appartiennent pas à ce noyau sont, quant à elles, rejetées.
À ce stade, il est cependant très difficile de conseiller le décideur quant à la solution optimale, et seul le rapprochement avec les méthodes d'agrégations a priori de critères en un critère unique permet de conclure quant au choix de la ville n°2.
Il est toutefois notable que la ville n°4, bien qu'appartenant au noyau, n'est pas une solution optimale, conformément aux méthodes précédentes.
Attention : la méthode développée ci-dessus, ELECTRE I, ne fonctionne pas s'il y a des circuits.
Limites et désavantages de cette méthode
Les avantages d'une méthode de surclassement telle ELECTRE sont :
- Simplicité de la méthode car elles reposent sur des concepts naturels, tels « d'accord » ou « pas d'accord ».
- Analyse de la robustesse très poussée qui compense le caractère subjectif de certains paramètres.
Néanmoins, le désavantage majeur inhérent à cette méthode est que le noyau ne renferme pas les meilleures actions mais celles qui sont les plus difficiles à comparer entre elles[5]. Le résultat fourni, sans autre méthode mathématique d'analyse multicritères, ne permet pas d'accéder directement aux meilleurs actions potentielles et des décisions erronées sont éventuellement possibles.
Notes et références
- Roy B. (1985). Méthodologie multicritères d’aide à la décision. Paris : Economica, XXII + 423 p.
- Analyse multicritères Par Nadia Lehoux et Pascale Vallée
- Roy B., Skalka JM. (1985). E l e c t re Is, aspects méthodologiques et guide d’utilisation. Document 30, Lamsade. Paris : Université de Paris Dauphine, 119p.
- Comment déterminer les poids
- Limites de l'analyse multicritère
- Intégrer une dimension écologique dans la planification territorial avec des méthodes d'analyse multicritère
Liens externes
- Mathieu Rouaud ; Probabilités, statistiques et analyses multicritères Un livre qui traite des approches multicritères (les principes et de nombreux exemples).
- Portail des mathématiques
- Portail de l’informatique
- Portail de l'informatique théorique