Mesure des distances en cosmologie
En cosmologie physique, la mesure des distances cosmologiques consiste à fournir la valeur d'une distance - ou un équivalent - entre deux objets ou évènements de l'Univers. On utilise souvent les mesures pour lier des quantités observables telles que la luminosité d'un quasar éloigné, le décalage vers le rouge d'une galaxie ou encore la dimension angulaire des pics acoustiques du spectre du fond diffus cosmologique, à une autre quantité qui n'est pas directement observable, mais est plus facile à calculer telles que les coordonnées comobiles des quasars, des galaxies, etc. La mesure des distances ainsi considérée se réduit finalement à la notion commune de distance euclidienne, donc à faible décalage vers le rouge.
Conformément à l'avancement des connaissances en cosmologie, on calcule ces mesures dans le contexte de la relativité générale, dans lequel c'est la métrique de Friedmann-Lemaître-Robertson-Walker qui décrit l'Univers.
Types de mesures des distances
Il existe différentes méthodes de mesure, selon les objets considérés et les données qu'il est possible de considérer à leur sujet :
- la distance en diamètre angulaire constitue une bonne indication (spécialement dans un univers plat) de la proximité à laquelle se trouvait un objet astronomique lorsqu'il a émis la lumière vue par un observateur terrestre ;
- la distance de luminosité s'appuie sur la quantité de lumière reçue d'un objet, en rapportant sa magnitude absolue () à sa magnitude apparente () ;
- la distance comobile entre deux points est mesurée le long d'un chemin défini selon le temps cosmologique présent ;
- la distance cosmologique propre entre deux points est mesurée le long d'un chemin défini selon un temps cosmologique constant. Il faut distinguer la distance cosmologique propre de la notion plus générale de longueur propre ou distance propre ;
- le temps de voyage de la lumière ou temps de regard vers le passé mesure la durée depuis laquelle la lumière a quitté un objet d'un décalage vers le rouge donné ;
- la distance de voyage de la lumière est égale au temps de voyage de la lumière multiplié par la vitesse de la lumière. Pour des valeurs supérieures à deux milliards d'années-lumière, cette valeur n'est plus égale à la distance comobile ou à la distance de diamètre angulaire du fait de l'expansion de l'univers[1] ;
- la loi de Hubble "naïve", qui pose , où H0 représente la constante de Hubble actuelle, z, le décalage vers le rouge de l'objet, c, la vitesse de la lumière, et d la "distance".
Comparaison des mesures de distances
Comparaison des mesures de distances cosmologiques, du décalage vers rouge z=0 jusqu'à z=0,5. La cosmologie sous-jacente retient les paramètres suivants :
|
- la distance de voyage de la lumière est égale à la vitesse de la lumière multipliée par l'intervalle de temps cosmologique, c'est-à-dire l'intégrale de c dt alors que la distance comobile est égale à l'intégrale de c dt /a(t).
- dL distance de luminosité ;
- dpm distance de mouvement propre :
- appelée distance de dimension angulaire par James Peebles en 1993, mais ne doit pas être confondue avec la distance de diamètre angulaire[2]
- parfois appelée distance coordonnée ;
- parfois également appelée distance de diamètre angulaire ;
- da distance de diamètre angulaire.
Les trois dernières mesures sont liées par la relation :
da = dpm / (1 + z) = dL /(1 + z)2,
où z correspond au décalage vers le rouge.
La relation entre la distance de luminosité des Chandelle standard et la distance de diamètre angulaire, da = dL /(1 + z)2, est aussi appelée équation de dualité des distances d'Etherington.
- Si et seulement si la courbure est nulle, la distance de mouvement propre et la distance comobile sont identiques, c'est-à-dire :.
- Pour une courbure négative :
,
- alors que pour une courbure positive :
,
où est la valeur absolue du rayon de courbure.
Une formule pratique d'intégration numérique de à un décalage vers le rouge pour des valeurs arbitraire de paramètre de densité de matière , la constante cosmologique , et le paramètre de la quintessence est :
où c est la vitesse de la lumière et H0 la constante de Hubble.
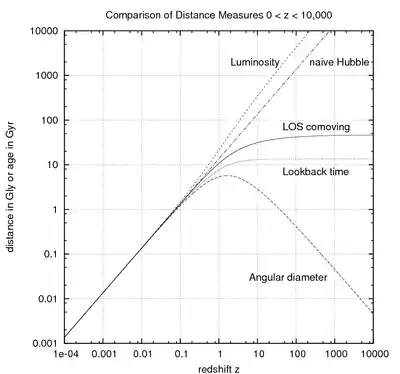
Comparaison des mesures de distance cosmologiques, depuis un décalage vers le rouge de zéro jusqu'à 10000 correspondant à l'époque de l'équivalence matière/rayonnement. La cosmologie sous-jacente retient les paramètres suivants :
|
L'utilisation des fonctions sinus et sinh permet d'obtenir la distance de mouvement propre dpm à partir de dp.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « distance measures (cosmology) » (voir la liste des auteurs).
- Sur la taille de l'unvivers visible, voir également l'article de l'encyclopédie anglaise traitant des erreurs conceptuelles sur les dimensions de l'univers (en)
- (en)SAO/NASA ADS Astronomy Abstract Service, sur le site u-strasbg.fr
Voir aussi
Bibliographie
- P. J. E. Peebles, Principles of Physical Cosmology. Princeton University Press (1993)
- Scott Dodelson, Modern Cosmology. Academic Press (2003).
- (en) Sherry H. Suyu, Tzu-Ching Chang, Frédéric Courbin et Teppei Okumura, « Cosmological Distance Indicators », Space Science Reviews, vol. 214, , p. 91- (DOI 10.1007/s11214-018-0524-3)
Articles connexes
Liens externes
- The Distance Scale of the Universe (L'échelle des distances de l'Univers) compare différentes mesures de distances cosmologiques.
- 'Distance measures in cosmology (Mesure des distances en cosmologie)' explique de façon détaillée comment calculer les différentes mesures de distance en fonction du modèle d'univers et du décalage vers le rouge.
- iCosmos: Cosmology Calculator (With Graph Generation) calcule les différentes mesures de distance en fonction du modèle cosmologique et du décalage vers le rouge, et génère un graphe pour le modèle entre de décalage vers le rouge de 0 à 20.
- Portail de la cosmologie
- Portail de l’astronomie