Modèle de Cross
Le modèle de Cross est un modèle de viscosité des polymères (rhéologie), qui permet à la fois de décrire un fluide newtonien, un fluide rhéofluidifiant ou rhéoépaississant, selon la valeur d'un des paramètres. Il a été proposé par Malcolm M. Cross en 1965[1].
Pour les articles homonymes, voir cross.
D'autre modèles ont été construits à partir de ce modèle : le modèle Cross-exp et le modèle Cross-WLF (Williams-Landel-Ferry).
Domaine d'application
Les polymères (matières plastiques, caoutchoucs) sont souvent mis en forme par extrusion, injection, soufflage. Le polymère est chauffé pour qu'il devienne pâteux ou liquide. L'effort qu'il faut fournir pour le faire avancer dans un canal ou pour le déformer dépend de sa viscosité dynamique η (lettre grecque êta). Et pour un effort donné, le débit de matière que l'on obtient dans un canal ou bien la manière dont le liquide « s'accroche » aux parois dépend aussi de η.
Phénomène de viscosité
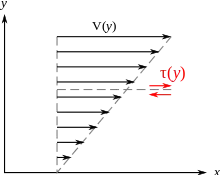
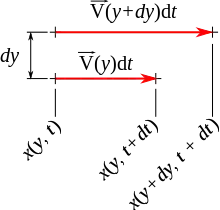
Un fluide visqueux a tendance à s'accrocher aux parois. Lors d'un écoulement, il y a donc un gradient de vitesse :
- à proximité de la paroi, la vitesse est parallèle à la paroi (le flux ne la traverse pas) ;
- lorsque l'on se rapproche de la paroi, la vitesse diminue.
La vitesse V augmente lorsque l'on s'éloigne perpendiculairement à la paroi. Cette différence de vitesse entre deux couches de fluide crée un effort de cisaillement τ.
Si la normale de la paroi est l'axe y et que l'écoulement se fait selon l'axe x d'un repère orthonormé, alors la viscosité dynamique est définie par la relation
Par ailleurs, ce gradient de vitesse crée un gradient de déplacement du. On définit le taux de cisaillement (gamma point) par
d'où .
Modèle de Cross
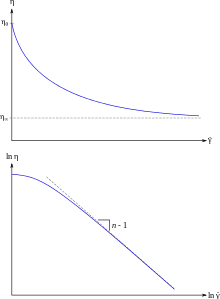
Le modèle de Cross et les modèles dérivés sont une expression de η en fonction du taux de cisaillement
où :
- k et m sont des constantes propres au fluide, définissant la forme de la courbe ;
- η0 est la viscosité pour un taux de cisaillement nul ;
- η∞ est l'asymptote viscosité pour un taux de cisaillement très élevé.
Ces paramètres sont propres au matériau et sont obtenus par des essais. Dans le modèle initial, M. M. Cross fixe la valeur de m à 2/3[1].
Ce modèle est également présenté sous une forme à trois paramètres
où λ est une constante de temps.
Notons que l'on reconnaît la loi en puissance d'Ostwald–de Waele pour les fluides non-newtoniens
avec 0 < n < 1 pour un fluide rhéofluidifiant.
On trace souvent le diagramme logarithmique. On a alors ce qui donne l'équation d'une droite de pente n - 1 pour les fortes valeurs de taux de cisaillement .
Modèle Cross-exp
Le modèle Cross-exp s'écrit
où τ* et n sont des paramètres constants caractéristiques du matériau, et η0, la viscosité pour un taux de cisaillement nul, est un paramètre dépendant de la pression p et de la température absolue T, sous la forme
où B, Tb et β sont des constantes dépendant du matériau. Le paramètre Tb est la sensibilité de η0 à la température, et dépend normalement lui-même de la température ; on le considère comme constant dans une gamme de températures donnée. Le paramètre β est la sensibilité de η0 à la pression, et dépend lui-même de la température et de la pression ; on le considère comme constant pour un domaine de température et de pression restreint.
Modèle Cross-WLF
Le modèle Cross-WLF s'écrit de la même manière que le modèle Cross-exp
mais la viscosité à taux de cisaillement nul η0 s'exprime différemment
avec
Les paramètres A1, A3, D1, D2 et D3 sont des constantes caractéristiques du matériau. Dans l'idéal, T* est la température de transition vitreuse Tv (ou Tg).
Dans un certain nombre de cas, on a D3 = 0, donc le comportement ne dépend pas de la pression (dans la gamme de pressions à laquelle on s'intéresse).
Références
- (en) Malcolm M. Cross, « Rheology of non-Newtonian fluids : A new flow equation for pseudoplastic systems », Journal of Colloid Science, Elsevier, vol. 20, no 5, (présentation en ligne)
Articles connexes
- Liste de modèles rhéologiques
- Loi de Carreau-Yasuda
- Loi d'Ostwald–de Waele, ou loi en puissance
- Portail de la chimie
- Portail de la physique