Ennéagone
Un ennéagone[1], ou nonagone[2],[3],[4], est un polygone à 9 sommets, donc 9 côtés et 27 diagonales.
| Ennéagone régulier | |
| |
| Type | Polygone régulier |
|---|---|
| Arêtes | 9 |
| Sommets | 9 |
| Symbole de Schläfli | {9} |
| Diagramme de Coxeter-Dynkin | |
| Groupe de symétrie | groupe diédral D18 |
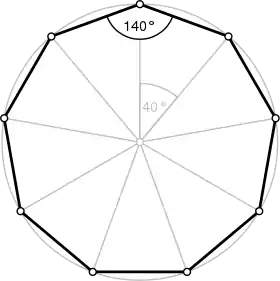
| Angle interne | 140° |
La somme des angles internes d'un ennéagone non croisé vaut 7π radians, soit 1 260 degrés.
Un ennéagone régulier est un ennéagone dont les neuf côtés ont la même longueur et dont les angles internes ont même mesure. Il y en a trois : deux étoilés (les ennéagrammes notés {9/2} et {9/4}) et un convexe, noté {9}. C'est de ce dernier qu'il s'agit lorsqu'on parle de « l'ennéagone régulier ».
Caractéristiques de l'ennéagone régulier
Si le côté a pour longueur a :
- chacun des 9 angles internes mesure 7π/9 rad = 140° ;
- chaque angle au centre mesure 2π/9 rad = 40° ;
- le rayon du cercle circonscrit vaut ;
- l'apothème (le rayon du cercle inscrit) est (a/2) cot(π/9) ;
- La grande diagonale a pour longueur ;
- l'aire est égale à.
Construction d'un ennéagone régulier
Un ennéagone régulier n'est pas constructible avec seulement une règle (non marquée) et un compas, car le nombre 9 ne satisfait pas la condition du théorème de Gauss-Wantzel. Il l'est, par contre, « par neusis », avec une règle marquée et un compas.
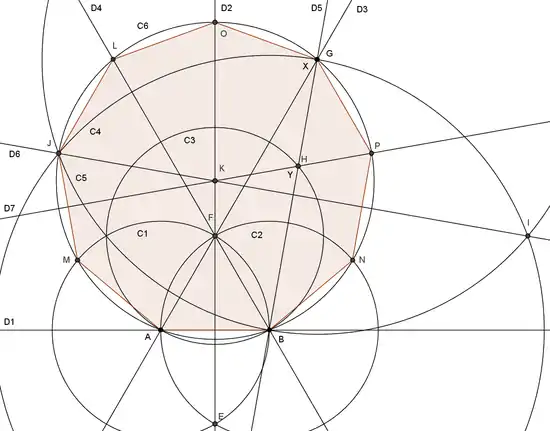
Pour construire un ennéagone régulier dont un des côtés est le segment AB, de longueur u, on procède ainsi[réf. souhaitée] :
- Appelons D1 la droite contenant A et B.
- Tracer les cercles C1 de centre A passant par B, et le cercle C2 de centre B passant par A. Ces deux cercles se coupent en deux points E et F, F étant le point du demi-plan d'origine D1 dans lequel on veut situer le centre de l'ennéagone.
- Tracer la droite D2 passant par E et F.
- Tracer le cercle C3 de centre F passant par A.
- Tracer les droites D3 et D4, passant par F et, respectivement, par A et B.
- Marquer la règle de deux points X et Y distants de u égal au segment AB qui est le côté du triangle équilatéral.
- Faire glisser la règle marquée en pivotant autour du point B et en maintenant la marque X sur D3, avec la marque Y entre X et B, jusqu'à ce que la marque Y de la règle se trouve sur le cercle C3, en un point H. La marque X se trouve alors en un point G sur la droite D3. Tracer la droite D5 passant par B, H et G.
- Tracer le cercle C4 de centre B passant par G, et le cercle C5 de centre G passant par B. Ces deux cercles se coupent en I et J, J étant le point situé dans le demi-plan d'origine D5 contenant A.
- Tracer la droite D6 passant par I et J. Elle coupe D2 en K.
- Tracer le cercle C6 de centre K passant par A. Il passe aussi par B, G et J.
- C6 coupe D2 en un point O dans le demi-plan d'origine D1 contenant K.
- C6 coupe D4, C1 et C2, en des points autres que les points A ou B, respectivement en L, M et N.
- Tracer la droite D7 passant par K et H. Elle coupe C6 en P dans le demi-plan d'origine D5 contenant N.
- Le polygone ABNPGOLJM est l'ennéagone recherché.
La démonstration complète est un peu longue mais relève de la géométrie élémentaire.
Architecture

Les remparts de Palmanova, en Italie, furent bâtis par les Vénitiens en suivant un plan circulaire où les neuf bastions occupent les sommets d'un ennéagone régulier.
Notes et références
- Denis Henrion, Mémoires mathématiques, (lire en ligne), p. 358.
- Michel Chasles, Aperçu historique sur l'origine et le développement des méthodes en géométrie, M. Hayez, (lire en ligne), p. 453, 480 et 484.
- Encyclopédie méthodique, Mathématiques, vol. 2, p. 468.
- Le mot « nonagone » associe un préfixe latin et un suffixe grec.
Voir aussi
Articles connexes
Liens externes
- G. Villemin, « Ennéagone », sur Nombres - Curiosités, théorie et usages
- (en) Eric W. Weisstein, « Trigonometry Angles — Pi/9 », sur MathWorld
- Ennéagone régulier : construction approchée sur geogebratube.org (précision 0,006 %)
- Constructions approchées d'un ennéagone régulier par l'IREM de l'université Montpellier 2
- Tracé de l'ennéagone (méthode approchée) sur le site du château de Mézerville (précision 1 %)
- Portail de la géométrie