Optimisation topologique
L'optimisation topologique est une méthode mathématique (et logicielle) qui permet de trouver la répartition de matière optimale dans un volume donné soumis à des contraintes. Elle se distingue notamment de l'optimisation de forme qui ne fait varier que la frontière de la pièce, qu'il faut avoir dessinée au départ[1].
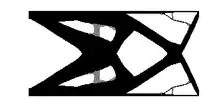
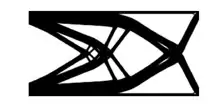
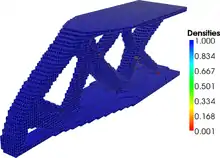
Les méthodes d'optimisation topologiques connues à ce jour permettent d'optimiser la résistance élastico-mécanique, la conductivité thermique ou certains problèmes d'écoulement fluide.
Histoire
Cette méthode issue des mathématiques a été clairement définie, expliquée et rendue exploitable pour la mécanique dans les années 2000, notamment avec l'article fondateur de Ole Sigmund[2].
Des logiciels d’optimisation topologique de plus en plus sophistiqués permettent aux ingénieurs d'économiser la matière possible d’un objet tout en conservant ou améliorant sa solidité ou sa souplesse (au besoin) et en tenant compte des contraintes qui s’exerceront sur lui, travail autrefois basé sur l’intuition, la méthode des essais et des erreurs et/ou le génie des créateurs et/ou des ingénieurs de fabrication[3].
Un exemple très simple est la réduction optimisée du nombre de rayons d’une roue de bicyclette[3]. Jusqu’ici seules des formes simples étaient concernées, car ces logiciels sont très gourmands en calcul ou étaient rapidement limités par la complexité du travail demandé[3].
En , dans la revue Nature[4], des chercheurs d’une université danoise présentent une méthode permettant de faire ce travail pour des objets de grande taille, en améliorant la résolution possible. Une image 2D est composée de pixels alors qu’une image 3D est composée de voxels. Jusqu’à il y a peu[Quand ?], la résolution des modèles 3D optimisés était limitée à 5 millions de voxels, mais un nouveau programme optimise des objets jusqu'à 1 milliard de voxels. Ceci permet par exemple de modéliser et reconcevoir une aile de Boeing 777 en l’optimisant : elle se trouve allégée de 5% et renforcée de l’intérieur par des longerons courbes et des nervures diagonales, et non plus par une structure en forme de grille. L'économie attendue est de 200 tonnes de kérosène/an[4]. 5 jours de calculs par un superordinateur ont été nécessaires, et ce design (qui évoque l’intérieur de certains os ou l'intérieur de parties d’exosquelettes d’insectes) est actuellement « infabricable ». Cependant, les progrès de l'impression 3D pourraient bientôt le mettre à notre portée[3],[4].
Formalisme mathématique
Énoncé
Le problème général d'optimisation topologique est posé comme
où
- La variable de conception (design) est la densité du matériau. 1 signifie présence de matériau et 0 signifie absence de matériau. La variable d'état est la solution à une équation différentielle qui modélise le phénomène en jeu, selon le design (généralement les équations d'élasticité);
- est la fonctionnelle coût. Elle représente une quantité d'intérêt qu'on veut minimiser ou maximiser (généralement la flexibilité ou la rigidité);
- est l'espace de conception, c'est-à-dire l'ensemble des points qui sont sujets à l'optimisation;
- Les contraintes permettent d'imposer des particularités à la forme finale. Par exemple, impose une contrainte sur la quantité maximale de matériau à avoir.

Interpolation des propriétés matérielles
Résoudre ce problème vise à déterminer une répartition optimale du matériau dans l'espace de conception . Le module de Young est la propriété qui quantifie la capacité d'un matériau à se déformer. Cette caractéristique doit être interpolée selon la densité (les endroits où il y a présence de matériau sont rigides, contrairement à ceux où il y a du vide). Par exemple, l'approche SIMP (Solid Isotropic Material with Penalization) utilise une loi de puissance pour déterminer le module de Young selon la densité en un point:
Le paramètre (typiquement[2] ) pénalise les valeurs entre 0 et 1 pour obtenir un résultat binaire. est pris très près de 0 pour représenter le vide, mais non nul pour éviter les termes nuls dans la matrice de résolution de la méthode des éléments finis.
D'autres approches sont utilisées[5], comme la méthode RAMP, qui passe par une interpolation rationnelle.
Caractérisation de l'optimalité
L'annulation du gradient en un point est une condition nécessaire à l'optimalité dans un problème sans contrainte. La dérivée au sens de Gateaux permet de calculer le gradient d'une fonctionnelle dans une direction :
Une solution analytique à ce problème est difficile à obtenir. Les méthodes numériques d'optimisation comme la descente du gradient utilisent pour obtenir des designs presque optimaux. Les contraintes peuvent être prises en compte dans ces algorithmes en utilisant diverses techniques de pénalisation.
Mise en œuvre
En mécanique, la résolution d'un problème d'optimisation topologique passe par la modélisation de la pièce, ou de l'ensemble de pièces, à optimiser par la méthode des éléments finis. Une méthode classique d'optimisation topologique consiste alors à considérer en tout point du volume d'optimisation une densité de matière variant entre 0 et 1. D'autres méthodes considèrent l'orientation locale du matériau (pour les matériaux non isotropes) ou même d'autres caractéristiques. Optimiser consiste généralement dans ces méthodes à minimiser l'énergie de déformation de la structure, ce qui revient à peu près à trouver la structure la plus rigide possible. On peut ainsi soit fixer la quantité de matière mise en œuvre pour mettre en avant des formes optimales, pour orienter un design et une optimisation faite par ailleurs, soit chercher directement à définir une forme minimisant la matière à mettre en œuvre pour alléger au maximum la structure, en respectant une contrainte à ne pas dépasser. En pratique, pour un résultat exploitable (car c'est un nuage de densité de matière qui est généré a priori et non pas un solide avec une frontière bien définie) il est ajouté des méthodes de pénalisation, de filtrage[6], et de seuillage [7], en particulier pour imposer les contraintes géométriques spécifiques liées au processus de fabrication (symétries, autorisation de volume creux ou non, …, plan de joint)[8].
Les principales étapes et difficultés à franchir sont généralement les suivantes :
- Définir le cahier des charges de la pièce à concevoir :
- Espace réellement disponible : il est souvent bien plus grand que la pièce éventuellement existante, et peut être encore agrandi en remettant à plat la fonction réellement à remplir et les contraintes environnantes à cette pièce, ou de l'ensemble de pièces à reconcevoir. Il ne faut pas oublier les zones où la matière est imposée ou interdite (pour des raisons fonctionnelles ou esthétiques).
- Liaisons mécaniques avec l'environnement : il faut bien remettre à plat les liaisons possibles avec les pièces voisines, car il y a souvent bien plus de liberté pour les zones de fixations que celles envisagées a priori. Il n'est parfois pas évident de distinguer quelles zones bloquer ou quelles zones sont chargées par des forces, le plus pragmatique étant alors d'imaginer comment pourrait être testée la pièce sur un banc d'essai, avec des liaisons fixes et des vérins, par exemple.
- Efforts mécaniques subis : il faut bien prendre en compte tous les chargements mécaniques vus par la pièce, au-delà de la fonction principale, c.-à-d. les efforts liés à des étapes de fabrication (notamment l'usinage), les efforts liés à la manipulation de la pièce (montage/démontage de la pièce, transport), les efforts accidentels (chocs), par exemple.
- Symétries et conditions de fabrication (cela étant de mieux en mieux pris en compte par les logiciels de calcul).
- Lancer le calcul d'optimisation topologique : il faut adapter la finesse du maillage à la précision spatiale recherchée et aux moyens informatiques dont on dispose ; les calculs peuvent être longs, on cherche donc à faire des premiers calculs à l'échelle de quelques minutes, pour les affiner ensuite. Il faut aussi bien vérifier comment sont pris en compte les différents cas de chargement par l'algorithme. En effet si l'on cherche juste la structure la plus rigide possible pour une masse donnée, les énergies des différents chargements sont simplement sommées, il convient alors de les pondérer entre eux, éventuellement. Par contre, si l'objectif est d'obtenir la pièce la plus légère possible qui ne casse pas, nul besoin de pondération.
- Analyse du résultat : Pour montrer une pièce facilement compréhensible (avec du vide et du plein bien définis), le résultat est généralement filtré par les logiciels pour l'affichage (par ex. le plein correspond aux zones de densité matière supérieures à 50%, sinon c'est du vide). Il faut donc bien prendre en compte qu'en général c'est une matière plus ou moins dense/poreuse qui est vraiment considérée par l'algorithme, et que les zones éventuelles de matière non reliée au reste sont tout à fait possibles, à l'affichage, car elles sont liées au reste par de la matière à faible densité, non affichée. Le résultat est donc à intreprêter pour définir une pièce faite de vide et de plein, au plus près de ce que l'algorithme propose. Il existe des paramètres (parfois cachés) pour explorer en détail ces subtilités : seuil d'affichage de la matière (par défaut 50% en général), pénalisation (paramètre limitant les zones de densités autour de 50%, mais pouvant dégrader la convergence des algorithmes), filtrage/lissage (filtre permettant d'éliminer des détails jugés trop petits), et bien sûr la finesse du maillage (qui permet de faire apparaître des détails plus ou moins fins). On se rend fréquemment compte à ce stade que la forme obtenue est absurde, généralement suite à l'oubli d'une contrainte majeure, ou car le problème était mal posé (par exemple s'il n'y a pas assez de liaisons au bâti pour maintenir la pièce, ou parce que des blocages ou des efforts ont été appliqués sur une zone où la matière est interdite).
- Dessin et vérification : une fois l'interprétation des résultats consolidée, la pièce peut être dessinée, aussi proche que possible de la topologie obtenue (nombre de barres/plaques, orientation, épaisseurs relatives), mais éventuellement plus agréable à l'œil, car les formes dites «organiques» obtenues par optimisation topologique ne conviennent pas toujours. C'est pourquoi on impose parfois une peau extérieure à la pièce (la partie visible) en limitant l'optimisation topologique uniquement à l'intérieur de la pièce à alléger (partie invisible). Il est optimum si possible d'utiliser des structures lattices (c.-à-d. un réseau serré de poutres ou de parois, comme des mousses), afin de mettre de la matière de densité intermédiaire là où le calcul la fait apparaître (c'est ainsi que la nature exploite des densités de bois différentes dans l'arbre, ou des densités d'os variables chez les vertébrés.
Références
- G. Allaire, S. Aubry, E. Bonnetier et F. Jouve, « Optimisation Topologique de Structures par Homogénéisation », (consulté le )
- (en) Sigmund O., « A 99 line topology optimization code written in Matlab », Struct Multidisc Optim 21, 120–127, Springer-Verlag 2001, (lire en ligne)
- Andrew Wagner (2017) Watch a supercomputer design a radical new wing for airplanes (Voir un supercalculateur radicalment redesigner une aile d’avion), publié 04 octobre 2017
- Niels Aage, Erik Andreassen, Boyan S. Lazarov & Ole Sigmund (2017) Giga-voxel computational morphogenesis for structural design| Nature|550,84–86 |05 Octobre 2017 |Doi:10.1038/nature23911|Mis en ligne le 04 Octobre 2017
- (en) Joshua D. Deaton et Ramana V. Grandhi, « A survey of structural and multidisciplinary continuum topology optimization: post 2000 », Structural and Multidisciplinary Optimization, vol. 49, no 1, , p. 1–38 (ISSN 1615-1488, DOI 10.1007/s00158-013-0956-z, lire en ligne, consulté le )
- Bourdin B (2001) Filters in topology optimization. Int. J. Numer. Methods Eng. 50, 2143–2158
- Catherine Vayssade, « Optimisation mécanique, Optimisation topologique », (consulté le )
- « L’optimisation topologique pour accélérer la conception », sur MetalBlog,
Voir aussi
Articles connexes
Liens externes
- Topopt Research Group, site d'un groupe de recherche universitaire très complet sur l'optimisation topologique.
- Topostruct, logiciel gratuit d'optimisation topologique.
- Inspire, logiciel commercial d'optimisation de structures, en particulier par optimisation topologique
- Animations d'optimisation topologique
- TOPOPTIM, procédure d'optimisation topologique implémentée dans le code éléments finis CAST3M
- OptiStruct, logiciel commercial d'optimisation de structures, en particulier par optimisation topologique
Bibliographie
- Aage N, Andreassen & Lazarov B.S(2015) Topology optimization using PETSc : an easy-to-use, fully parallel, open source topology optimization framework. Struct. Multidiscipl. Optim. 51, 565–572
- Alexandersen J, Sigmund O & Aage N (2016) Large scale three-dimensional topology optimisation of heat sinks cooled by natural convection. Int. J. Heat Mass Transfer 100, 876–891 |PDF, 24p
- Amir O, Aage N & Lazarov B.S (2014) On multigrid-CG for efficient topology optimization. Struct. Multidiscipl. Optim. 49, 815–829
- Alexandersen J & Lazarov B (2015) Topology optimisation of manufacturable microstructural details without length scale separation using a spectral coarse basis preconditioner. Comput. Methods Appl. Mech. Eng. 290, 156–182
- Bell J.H (2011) Pressure-sensitive paint measurements on the NASA Common Research Model in the NASA 11-ft transonic wind tunnel. In 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition 1128 (AIAA)
- Bendsøe M.P, Sigmund O, Bendsøe M.P & Sigmund O (2004). Topology optimization by distribution of isotropic material (pp. 1-69). Springer Berlin Heidelberg.
- Bendsøe M.P & Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 71, 197–224
- Bendsøe M.P & Sigmund O (2004) Topology Optimization — Theory, Methods and Applications (Springer)
- Bruns T.E & Tortorelli D.A (2001) Topology optimization of non-linear elastic structures and compliant mechanisms. Comput. Methods Appl. Mech. Eng. 190, 3443–3459 |résumé
- Cavazzuti, M. et al. (2011) High performance automotive chassis design: a topology optimization based approach. Struct. Multidiscipl. Optim. 44, 45–56
- Chin T & Kennedy G (2016) Large-scale compliance-minimization and buckling topology optimization of the undeformed Common Research Model wing. In 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 0939 (AIAA)|résumé
- Evgrafov, A., Rupp, C. J., Maute, K. & Dunn, M. L. (2008) Large-scale parallel topology optimization using a dual-primal substructuring solver. Struct. Multidiscipl. Optim. 36, 329–345 |résumé
- Groen J.P & Sigmund O. (2017) Homogenization-based topology optimization for high-resolution manufacturable microstructures. Int. J. Num. Methods Eng. https://doi.org/10.1002/nme.5575%7Crésumé
- Helms, H. & Lambrecht, U. (2007) The potential contribution of light-weighting to reduce transport energy consumption. Int. J. Life Cycle Assess. 12, 58–64
- Jensen, J. S. & Sigmund, O. (2011) Topology optimization for nano-photonics. Laser Photonics Rev. 5, 308–321 |résumé
- Kennedy, G. & Martins, J. A (2012) Comparison of metallic and composite aircraft wings using aerostructural design optimization. In 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference 5475, https://arc.aiaa.org/doi/abs/10.2514/6.2012-5475 (AIAA)
- Kenway G.K.W, Kennedy G.J & Martins J (2014) Scalable parallel approach for high-fidelity steady-state aeroelastic analysis and adjoint derivative computations. AIAA J. 52, 935–951
- Nomura T, Sato K, Taguchi K, Kashiwa T & Nishiwaki S (2007) Structural topology optimization for the design of broadband dielectric resonator antennas using the finite difference time domain technique. Int. J. Numer. Methods Eng. 71, 1261–1296|résumé
- Rao J, Kiran S, Kamesh J, Padmanabhan M & Chandra S (2009) Topology optimization of aircraft wing. J. Aerosp. Sci. Technol. 61, 402–414
- Saad Y (2003) Iterative Methods for Sparse Linear Systems Ch. 9.4.1 (SIAM)
- Stanford B & Dunning P (2014) Optimal topology of aircraft rib and spar structures under aeroelastic loads. J. Aircr. 52, 1298–1311
- Sardan O et al. (2015) Rapid prototyping of nanotube-based devices using topology-optimized microgrippers. Nanotechnology 19, 495503 (2008)
- Sigmund O.A (2001) 99 line topology optimization code written in Matlab. Struct. Multidiscipl. Optim. 21, 120–127
- Tortorelli D.A & Michaleris P (1994)Design sensitivity analysis: overview and review. Inverse Probl. Eng. 1, 71–105
- Wolff J The Law of Bone Remodeling (Springer, 1986) [transl.]
- Zhu, J., Zhang, W. & Xia, L. (2008) Topology optimization in aircraft and aerospace structures design. Arch. Comput. Methods Eng. 23, 1–28 (2015)
- Portail du génie mécanique