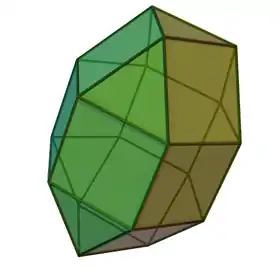
Orthobicoupole hexagonale allongée

En géométrie, l'orthobicoupole hexagonale allongée est un des solides de Johnson (J₃₅). Comme son nom l'indique, il peut être construit en allongeant une orthobicoupole hexagonale (J₂₇), c'est-à-dire en insérant un prisme hexagonal entre ses deux moitiés. Le solide résultant est similaire au rhombicuboctaèdre (un solide d'Archimède), avec la différence qu'il possède une symétrie rotationnelle triple sur son axe au lieu d'une symétrie quadruple.

Pour les articles homonymes, voir J35.

Orthobicoupole hexagonale allongée
Type	Orthobicoupole allongée J34 - J35 - J36
Sommets	18
Arêtes	36
Faces	(nombre : 20) 8 t 12 c
Configuration faciale	6 de 3.4.3.4 12 de 3.43
Groupe symétrique	D3h
Dual	-
Propriétés	convexe

Le volume de J₃₅ peut être calculé comme suit :

J₃₅ est constitué de 2 coupoles et 1 prisme hexagonal.

Les deux coupoles forment 1 cuboctaèdre = 8 tétraèdres + 6 demi-octaèdres. 1 octaèdre = 4 tétraèdres, donc au total nous avons 20 tétraèdres.

Quel est le volume d'un tétraèdre ? Construisons un tétraèdre ayant des sommets dans un cube (de côté ${\displaystyle {\frac {1}{\sqrt {2}}}}$, si le tétraèdre possède des arêtes unitaires). Les quatre pyramides triangulaires laissées si le tétraèdre est enlevé du cube forme un demi-octaèdre = 2 tétraèdres. Donc

${\displaystyle V_{tetraedre}={\frac {1}{3}}V_{cube}={\frac {1}{3}}{\frac {1}{{\sqrt {2}}^{3}}}={\frac {\sqrt {2}}{12}}}$

Le prisme hexagonal est plus direct. L'hexagone est d'aire ${\displaystyle 6{\frac {\sqrt {3}}{4}}}$, donc

${\displaystyle V_{prisme}={\frac {3{\sqrt {3}}}{2}}}$

Finalement

${\displaystyle V_{J_{35}}=20V_{tetraedre}+V_{prisme}={\frac {5{\sqrt {2}}}{3}}+{\frac {3{\sqrt {3}}}{2}}}$

Valeur numérique :

${\displaystyle V_{J_{35}}=4,9550988153084743549606507192748}$

Les 92 solides de Johnson ont été nommés et décrits par Norman Johnson en 1966.