Pérovskite (structure)

La pérovskite, du nom du minéralogiste russe L. A. Perovski, est une structure cristalline commune à de nombreux oxydes. Ce nom a d'abord désigné le titanate de calcium de formule CaTiO₃, avant d'être étendu à l'ensemble des oxydes de formule générale ABO₃ présentant la même structure. Les pérovskites présentent un grand intérêt en raison de la très grande variété de propriétés que présentent ces matériaux selon le choix des éléments A et B : ferroélasticité (par exemple SrTiO₃), ferroélectricité (par exemple BaTiO₃), antiferroélectricité (par exemple PbZrO₃), ferromagnétisme (par exemple YTiO₃), antiferromagnétisme (LaTiO₃), etc.

Structure pérovskite

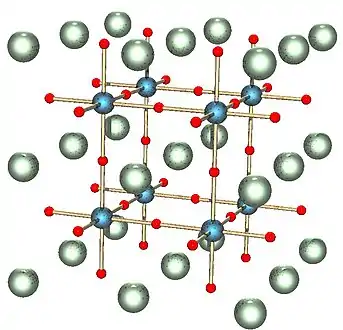
Pérovskite comme structure cristalline

Pérovskite idéale cubique

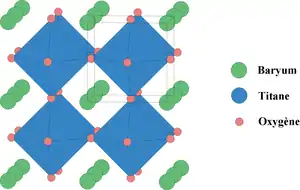
Exemple de structure pérovskite cubique : BaTiO₃ à haute température[1].

La structure pérovskite de plus haute symétrie est une structure de symétrie cubique. C'est par exemple la structure du titanate de baryum BaTiO₃ à haute température (voir figure ci-contre).

Dans la structure pérovskite cubique, les anions (ici O²⁻) forment un réseau d'octaèdres liés par leurs sommets. Le centre de chaque octaèdre est appelé site B. Il est occupé par un cation, dans cet exemple Ti⁴⁺. Le cation B présentera donc une coordinence 6. Les espaces entre les octaèdres sont des cuboctaèdres dont le centre constitue le site A. La coordinence des cations A est 12, en effet ils se trouvent sur un site à environnement anticuboctaédrique d'oxygène (le baryum dans la figure).

Pérovskites de plus basses symétries

Les pérovskites s'écartent souvent de cette structure cubique idéale. Cela est possible de plusieurs manières :

distorsion de l'ensemble de la maille, par exemple, un allongement dans une direction cristallographique particulière ;
décalage de l'ion A du centre du cuboctaèdre, ou de l'ion B du centre de l'octaèdre ;
rotation des octaèdres autour d'un axe ;
déformation des octaèdres.

De la sorte, les pérovskites peuvent présenter une grande variété de symétries différentes.

Facteur de tolérance de Goldschmidt

La flexibilité de la structure pérovskite se prête à une grande variété de substitutions, selon le choix des atomes sur les sites A et B. Particulièrement la relation entre les longueurs des sous-réseaux A et B joue un rôle important dans la détermination des propriétés de ces matériaux. Cette relation est souvent caractérisée par le facteur de tolérance de Goldschmidt, t. Dans la structure idéale, où les atomes se touchent les uns les autres, la distance B-O est égale à ${\frac {a}{2}}$ (où $a$ désigne le paramètre de la maille cubique), tandis que la distance A-O est ${\frac {a}{\sqrt {2}}}$ , donnant lieu à cette relation entre les rayons ioniques ${\textstyle r_{\mathrm {A} }+r_{\mathrm {O} }=(r_{\mathrm {B} }+r_{\mathrm {O} }){\sqrt {2}}}$ . Cette égalité n'est cependant pas exactement obéie dans les composés ABO₃. Le facteur de tolérance de Goldschmidt mesure la déviation par rapport à la situation idéale d'empilement compact des atomes et permet d'avoir une idée de la stabilité de la structure pérovskite en fonction des rayons des ions A, B et O :

t={\frac {r_{\mathrm {A} }+r_{\mathrm {O} }}{(r_{\mathrm {B} }+r_{\mathrm {O} }){\sqrt {2}}}}

.

Une liste d’ions qui forment la plupart des pérovskites, avec leurs rayons ioniques, est donnée dans le Tableau 1 et le Tableau 2 présente quelques pérovskites et leurs facteurs de tolérance.

Expérimentalement, la structure pérovskite est stable pour 0,88 < t < 1,10 ce qui permet une grande variété de substitutions sur les sites A et B et par conséquent l'existence d'un grand nombre de composés ayant cette structure. Selon la valeur de t, on observe des modifications structurales plus ou moins importantes par rapport à la structure prototype cubique. Pour un empilement parfait de sphères, on a $t\simeq 1$ donc un diélectrique sans polarisation, comme BaZrO₃. Le facteur t s'écarte de 1 quand les ions sont trop gros ou trop petits pour réaliser un empilement parfait. Plus la valeur du facteur de Goldschmidt s'éloigne de 1, plus la maille est déformée.

Si la limite $t=0.84$ est dépassée, la structure pérovskite 3D n’est plus stable et on obtient des phases en couches de type LiNbO₃. Le relâchement des contraintes impose des distorsions du réseau notamment des rotations des octaèdres BO₆, que l’on nommera par la suite par le mot anglais tilting. Les octaèdres BO₆ tournent autour des axes cristallographiques de plus haute symétrie afin de diminuer les contraintes. Des études structurales détaillées sur un très grand nombre de composés pérovskites ont été réalisées d’abord par A.M. Glazer [2]^,[3] puis par P. Woodward [4]^,[5]. Ces auteurs ont notamment caractérisé et classifié les directions des tiltings possibles selon une nomenclature qui tient compte du nombre d’axes de rotation des octaèdres. Il existe deux types de brisure de symétrie. Celle-ci peut être induite soit par une modification des directions du tilting des octaèdres BO₆ soit par un déplacement des cations comme dans le cas des composés à transition ferroélectrique.

Les transitions de phase des pérovskites lorsque la température varie sont bien connues. On peut citer le cas d’école BaTiO₃ qui est cubique à haute température et qui devient successivement quadratique puis orthorhombique et enfin rhomboédrique lorsque la température diminue [6].

Tableau 1. Les cations les plus communs qui forment les oxydes de structure pérovskite et leurs rayons ioniques Ref. [9]: $^{a}$ Coordination 7 ; $^{b}$ : Coordination 8.
Site du cation A	Rayon ionique (A°) pour O²⁻[7]	Site du cation B	Rayon ionique (A°) pour O²⁻[8]
Bi³⁺	1,11	Ti⁴⁺	0,605
Na⁺	1,32	Nb⁵⁺	0,64
Ca²⁺	1,35	Fe³⁺	0,645
Sr²⁺	1,44	Ta⁵⁺	0,68
Pb²⁺	1,49	Zr⁴⁺	0,72
Ba²⁺	1,6	Sc³⁺	0,73
K⁺	1,6	Pb⁴⁺	0,775

Tableau 2. Quelques composés pérovskites et leurs facteurs de tolérance (calculés selon la référence [9]).
Oxyde pérovskite	Facteur de tolérance $t$
BiScO₃	0,874
BiFeO₃	0,913
SrZrO₃	0,942
PbZrO₃	0,943
CaTiO₃	0,946
NaNbO₃	0,972
PbTiO₃	1,001
SrTiO₃	1,001
BaTiO₃	1,063
KTaO₃	1,085
KNbO₃	1,090

Pérovskite silicatée

La pérovskite silicatée est le minéral majeur du manteau inférieur[10].

Cristallochimie de la pérovskite Al-(Mg,Fe)SiO₃

La pérovskite magnésienne et alumineuse, Al-(Mg,Fe)SiO₃, apparaît dans le manteau inférieur à des profondeurs supérieures à 670 km. Ce minéral représente plus de 80 % en poids du manteau inférieur, ce qui en fait la phase la plus abondante de notre planète.

Trois phases pérovskites de compositions chimiques distinctes sont susceptibles d'apparaître dans le manteau inférieur : les composés (Mg,Fe)SiO₃, Al-(Mg,Fe)SiO₃ et CaSiO₃. La diffusion atomique permettra aux deux premiers composés de réagir entre eux pour n'en former qu'un, après un certain délai de résidence dans le manteau.

La pérovskite (Mg,Fe)SiO₃ adopte une symétrie orthorhombique dans une large gamme de pression, de température et de composition chimique. Cette phase s'appelle la bridgmanite. La phase CaSiO₃ est, quant à elle, de symétrie cubique.

Propriétés de la pérovskite Al-(Mg,Fe)SiO₃

Son équation d'état définit en particulier sa densité à toutes les conditions de pression et de températures régnant dans le manteau inférieur. Avec un module d'incompressibilité, K₀, d'environ 260 GPa, la pérovskite MgSiO₃ est un des minéraux les plus incompressibles.

La présence de fer induit une faible augmentation du volume de maille de la pérovskite Al-(Mg,Fe)SiO₃, une augmentation de la masse molaire, et donc de la densité, sans modifier significativement les paramètres élastiques de la structure. L'effet de l'aluminium est plus subtil et reste controversé.

L'oxygène semble être l'espèce atomique qui diffuse le plus rapidement dans la phase pérovskite, bien plus facilement que le silicium et l'aluminium.

Stabilité de la pérovskite Al-(Mg,Fe)SiO₃ à la base du manteau

Les études expérimentales de compressibilité montrent que la distorsion de la phase Al-(Mg,Fe)SiO₃ pérovskite augmente régulièrement avec la profondeur. Ceci est dû à une compression plus importante de la cage perovskite (et non le site dodécaédrique qui est une figure à 15 côtés formée de pentagones) (Mg,Fe)O₁₂ par rapport au site octaédrique SiO₆. Pour des pressions supérieures à 100 GPa, un autre arrangement dit post-pérovskite, de structure CaIrO₃, apparaît.

Cette transformation se produit à proximité de la frontière entre le noyau et le manteau et certaines anomalies sismiques observées dans la couche D″ à la base du manteau pourraient être expliquées par cette transition et par les propriétés spécifiques de cette phase postpérovskite.

Voir l'article Modèle PREM

Applications

Les pérovskites trouvent une large application dans l’électronique moderne en raison de leur forte permittivité diélectrique, de leur coefficient piézoélectrique élevé [11]^,[12], de leur ferroélectricité [13]^,[14], de leur semi-conductivité [15], de leur activité catalytique [16] et de leur thermoélectricité [17].

Ces propriétés se prêtent à de nombreuses applications technologiques dont les guides d’ondes optiques, les sondes à oxygène à haute température, les dispositifs d'onde acoustique de surface, les mémoires dynamiques à accès sélectif, les doubleurs de fréquence, les matériaux piézoélectriques déclencheurs et les condensateurs high-K [18]^,[19]. Dans le domaine de l’optoélectronique, une utilisation en tant que diélectrique pour la fabrication des condensateurs multicouches, des thermistances, des transducteurs, et aussi en tant que capacité intégrée dans le circuit CMOS (Complementary Metal Oxyde Semiconductor) pour gagner en compacité dans les téléphones mobiles, les microsystèmes résonants pour scanners optiques, résonateur acoustique pour les communications, capteur infrarouge pour caméras nocturnes ou encore mémoires de stockage non volatiles, mais aussi dans les appareils à microondes, et les manomètres.

Au Japon, un train à sustentation magnétique et des câbles électriques de réseaux de distribution urbains utilisent déjà les propriétés supraconductrices des pérovskites [20]. Ces matériaux très prometteurs trouvent de plus des applications dans les céramiques transparentes, les colorants non polluants PLZT (lead-Lanthanum-Zirconate-Titanate), cellules photovoltaïques où notamment le coût est réduit, également dans les piles à combustible. Les pérovskites avec des possibilités d'utilisation quasi universelles sont appelés les caméléons chimiques.

Ces oxydes à structure pérovskite sont donc des candidats prometteurs dans le développement de nouveaux matériaux ; toutefois avec certaines limitations tel que des courants de fuite élevés, une forte dépendance de la température et de la tension appliquée pour la capacité électronique, une température d'élaboration élevée, généralement supérieure à 400 °C, quelle que soit la technique de dépôt [21].

Quelques applications des matériaux pérovskites
Propriétés		Applications
Pyroélectricité		Détecteurs thermiques Imageurs IR
Piézoélectricité	directe	Déformation $\rightarrow$ Champ électrique : Générateurs d'impulsion haute tension (allumage des gaz, briquets) Capteurs (accéléromètres, imageurs IR, télécommande, microphones, hydrophones)
	inverse	Champ électrique $\rightarrow$ Déformation : Transducteurs ultrasonores de puissance (nettoyage ultrasonore, projecteurs sonar en acoustique sous-marine) Actuateurs Moteurs piézoélectriques (ultrasonore) Imprimante jet d'encre
	mixte	Capteur sonar Filtres électromécaniques
Ferroélectricité		Condensateurs Déphaseurs HF Filtres ultrasonores Transducteurs ultrasonores Mémoires non volatiles Diodes optiques Doubleurs Modulateurs
Antiferroélectricité		Transducteurs Condensateurs de stockage d'énergie

Notes et références

ICSD No. 43125 ; (en) F.J. Gotor, C. Real, M.J. Dianez et J.M. Criado, « Relationships between the Texture and Structure of BaTiO₃ and Its Tetragonal → Cubic Transition Enthalpy », Journal of Solid State Chemistry, vol. 123, n^o 2,‎ 1996, p. 301–305 (DOI 10.1006/jssc.1996.0183)
A.M. Glazer, « Acta Cryst. A 31 », 756,‎ (1975).
A.M. Glazer, « Acta Cryst. B 28 », 3384,‎ (1972).
P. Woodward, « Acta Cryst. B 53 », 44,‎ (1997).
P. Woodward, « Acta Cryst. B 53 », 32,‎ (1997).
G. Burns et A.M. Glazer, Space groups for solid state scientists, Academic Press, New York, 1978.
W. Cochran, « Adv. Phys. 9 », 387,‎ (1960).
D. M. Smyth, « Annu. Rev. Mater. Sci. 15 », 329,‎ (1985).
« Tolerance Factor Calculator »
(fr) Brunet et al, La Terre interne, roches et matériaux en conditions extrêmes, Vuibert, p. 140-149, (ISBN 978-2-7117-5397-0)
R. E. Eitel, C. A. Randall, T. R. Shrout, P. W. Rehrig, W. Hackenberger et S.-E. Park, « Jpn, J. Appl. Phys., Part 1 40 », 5999,‎ (2001).
S. J. Zhang, R. Xia, C. A. Randall, T. R. Shrout, R. R. Duan, et R. F. Speyer, « J. Mater. Res. 20 », 2067,‎ (2005).
J. G. Bednorz et K. A. Muller, « Phys. Rev. Lett. 52 », 2289,‎ (1984).
C. B. Samantaray, H. Sim, et H. Hwang, « Physica B 351 », 158,‎ (2004).
H. P. R. Frederikse, W. R. Thurber, and W. R. Hosler, « Phys. Rev. 134 », A442,‎ (1964).
C. S. Koonce, M. L. Cohen, J. F. Schooley, W. R. Hosler, et E. R. Pfeiffer, « Phys. Rev.163 », 380,‎ (1967).
V. E. Henrich, « Rep. Prog. Phys. 48 », 1481,‎ (1985).
V. E. Henrichand et P. A. Cox, The Surface Science of Metals Oxides, Cambridge University Press, New York, (1994).
E. Mete, R. Shaltaf, et S. Ellialtioglu, « Phys. Rev. B 68 », 035119,‎ (2003).
EMPA Dübendorf, « St-Gall », Thoune,‎ 7 septembre 2005.
Guillan, J, Etude de capacités en couches minces à base d'oxydes métalliques à très forte constante diélectrique, BaTiO3, SrTiO3 et SrTiO3/BaTiO3 déposées par pulvérisation par faisceau d'ions., Université Joseph Fourier, 2005, 266 p.

(de) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en allemand intitulé « Perowskit » (voir la liste des auteurs).

Voir aussi

Bibliographie

(en) Roger H. Mitchell, Perovskites : Modern and ancient, Almaz Press, 2002, 318 p. (ISBN 0-9689411-0-9)

Articles connexes

Facteur de tolérance de Goldschmidt (en)

Portail des minéraux et roches
Portail de la chimie
Portail de la physique
Portail des sciences des matériaux

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] ICSD No. 43125 ; (en) F.J. Gotor, C. Real, M.J. Dianez et J.M. Criado, « Relationships between the Texture and Structure of BaTiO₃ and Its Tetragonal → Cubic Transition Enthalpy », Journal of Solid State Chemistry, vol. 123, n^o 2,‎ 1996, p. 301–305 (DOI 10.1006/jssc.1996.0183)

[2] A.M. Glazer, « Acta Cryst. A 31 », 756,‎ (1975).

[3] A.M. Glazer, « Acta Cryst. B 28 », 3384,‎ (1972).

[4] P. Woodward, « Acta Cryst. B 53 », 44,‎ (1997).

[5] P. Woodward, « Acta Cryst. B 53 », 32,‎ (1997).

[6] G. Burns et A.M. Glazer, Space groups for solid state scientists, Academic Press, New York, 1978.

[7] W. Cochran, « Adv. Phys. 9 », 387,‎ (1960).

[8] D. M. Smyth, « Annu. Rev. Mater. Sci. 15 », 329,‎ (1985).

[9] « Tolerance Factor Calculator »

[10] (fr) Brunet et al, La Terre interne, roches et matériaux en conditions extrêmes, Vuibert, p. 140-149, (ISBN 978-2-7117-5397-0)

[11] R. E. Eitel, C. A. Randall, T. R. Shrout, P. W. Rehrig, W. Hackenberger et S.-E. Park, « Jpn, J. Appl. Phys., Part 1 40 », 5999,‎ (2001).

[12] S. J. Zhang, R. Xia, C. A. Randall, T. R. Shrout, R. R. Duan, et R. F. Speyer, « J. Mater. Res. 20 », 2067,‎ (2005).

[13] J. G. Bednorz et K. A. Muller, « Phys. Rev. Lett. 52 », 2289,‎ (1984).

[14] C. B. Samantaray, H. Sim, et H. Hwang, « Physica B 351 », 158,‎ (2004).

[15] H. P. R. Frederikse, W. R. Thurber, and W. R. Hosler, « Phys. Rev. 134 », A442,‎ (1964).

[16] C. S. Koonce, M. L. Cohen, J. F. Schooley, W. R. Hosler, et E. R. Pfeiffer, « Phys. Rev.163 », 380,‎ (1967).

[17] V. E. Henrich, « Rep. Prog. Phys. 48 », 1481,‎ (1985).

[18] V. E. Henrichand et P. A. Cox, The Surface Science of Metals Oxides, Cambridge University Press, New York, (1994).

[19] E. Mete, R. Shaltaf, et S. Ellialtioglu, « Phys. Rev. B 68 », 035119,‎ (2003).

[20] EMPA Dübendorf, « St-Gall », Thoune,‎ 7 septembre 2005.

[21] Guillan, J, Etude de capacités en couches minces à base d'oxydes métalliques à très forte constante diélectrique, BaTiO3, SrTiO3 et SrTiO3/BaTiO3 déposées par pulvérisation par faisceau d'ions., Université Joseph Fourier, 2005, 266 p.