Paysage adaptatif

Le paysage adaptatif (ou paysage de fitness, fitness landscape en anglais) est un outil utilisé en biologie évolutive pour visualiser les relations entre des génotypes et le succès reproductif. Le paysage adaptatif est une représentation de la fitness d’organismes, d’espèces ou de populations sous forme d’une carte topographique. Cette fitness, ou valeur sélective[1], est une mesure relative de la survie et de la reproduction.

Croquis d'un paysage de fitness. Les flèches indiquent le flux préférentiel d'une population dans le paysage, et les points A et C sont des archétypes locaux. Le cercle rouge correspond à une population ayant migré depuis une valeur de fitness très faible au sommet d'un pic.

Le paysage adaptatif est représenté sur deux axes. L’axe vertical représente la valeur de fitness. Si l’axe vertical représente la fitness des organismes, l’axe horizontal peut représenter soit le génotype soit le phénotype de ceux-ci. Si l’axe vertical représente plutôt la fitness des populations, l’axe horizontal représente alors la fréquence d’allèles ou de certains traits phénotypiques. Les génotypes similaires entre eux sont dits "proches" les uns des autres, alors que ceux qui sont très différents sont "éloignés" les uns des autres. L'ensemble de tous les génotypes possibles, leur degré de similarité et leurs valeurs de fitness associées est appelé un paysage adaptatif. L'idée d'un tel paysage est une métaphore aidant à expliquer les "formes imparfaites" issues de la sélection naturelle au cours de l'évolution, y compris les "améliorations" et les "déformations" chez les animaux comme leurs réactions aux stimuli supranormaux[2].

Histoire

L’idée d’un paysage adaptatif a été introduite pour la première fois en 1932 par Sewall Wright au 6e Congrès International de la Génétique[3],[4]. Il voulut créer cette métaphore pour visualiser le processus de l’évolution, et plus particulièrement les facteurs impliqués tels que la dérive génétique et la sélection naturelle.

Wright introduit deux types de paysages adaptatifs dans sa première publication sur le sujet[5]. Le premier type représente la fitness d’organismes en fonction de leur génotype ou phénotype, et le deuxième type représente la fitness des populations en fonction de la fréquence d’allèles ou de certains traits phénotypiques[6].

Wright fut longtemps en débat avec Fisher en ce qui concerne l’importance relative de la dérive génétique par rapport aux autres facteurs influençant l’évolution. Wright apportait une grande importance à la dérive génétique, même plus qu’à la sélection naturelle.

Sa théorie de « shifting balance », appelée en français théorie des glissements d'équilibre[7], utilise la dérive génétique pour expliquer comment les espèces peuvent continuer à évoluer vers une fitness plus élevée, même une fois qu’elles sont bien adaptées à leur environnement. Selon lui, les espèces devraient d’abord passer à travers des stages intermédiaires, mal adaptés. Ces stages sont représentés dans le paysage adaptatif comme les vallées entre les pics. Si elle est assez petite, une population passerait d’un pic à une vallée par la dérive génétique. S’il y a un flux génétique entre les populations, ces adaptations s’étendraient à travers l’espèce[6].

L’idée d’un paysage adaptatif pour expliquer l’évolution a toujours été controversée, toutefois il s’agit d’un bon outil pour comprendre l’importance des facteurs comme la sélection et la dérive génétique dans le processus de l’évolution.

Organisation d’un paysage adaptatif

Dans tout paysage adaptatif, le sommet des pics représente une valeur maximale de fitness. Les points peuvent représenter soit des organismes individuels ou des populations. Dans le cas où les points représentent des organismes, les nuages de points représenteraient les populations. Les pics représentent donc des espèces différentes, puisqu’il s’agit des organismes les plus adaptés, du moins localement, qui les forment. Les vallées entre les pics ont des valeurs de fitness moindres. Elles représentent donc des hybrides mal adaptés à leur environnement[8].

Du génotype au paysage de fitness
Représentation de deux dimensions d'un paysage de fitness NK. Les flèches représentent diverses voies mutationnelles que la population pourrait suivre lors de son évolution dans le paysage de fitness.

Wright a visualisé un espace génotypique comme un hypercube[3] dans lequel aucune « dimension » génotypique continue n'est définie. Au lieu de ça, les génotypes sont connectés en réseau via des chemins mutationnels.

Le modèle NK de Stuart Kauffman est un modèle d'optimisation combinatoire au paysage configurable. Le modèle NK intègre des relations d'Épistasies entre les variables qui influent sur l'espace de recherche du problème. De nouvelles techniques d'analyse de réseau, comme le graphique d'attraction pondéré par sélection (selection-weighted attraction graphing ou SWAG en anglais), utilisent également un espace génotypique sans dimension[9].

De la fréquence allélique aux paysages de fitness

Le travail mathématique de Wright a décrit la fitness comme une fonction des fréquences alléliques[10].

Du phénotype aux paysages de fitness

Dans le troisième cas de paysage de fitness, chaque dimension représente un trait phénotypique différent[11]. Sous les hypothèses de la génétique quantitative, ces dimensions phénotypiques peuvent être cartographiées sur des génotypes. Voir les représentations ci-après pour des exemples de paysages de fitness représentant des phénotypes.


Bouger dans un paysage adaptatif

Le mouvement dans un paysage adaptatif représente le processus de l’évolution. Les organismes ou populations peuvent bouger à travers le paysage adaptatif selon les principes fondés sur la théorie « shifting-balance ». Ce serait donc la dérive génétique qui permet à une sous-population déjà adaptée, soit au sommet d’un pic, de descendre vers une vallée. Par ce processus, l’espèce devient mal adaptée à son environnement. En considérant uniquement la sélection naturelle, cela ne serait jamais possible. Une fois dans la vallée, la sous-population se dirige vers la base d’un pic encore plus haut que le précédent. Elle va ensuite commencer à grimper le pic par sélection naturelle[11]. Ici, chaque dimension décrit une fréquence allélique d'un gène différent, et se situe entre 0 et 1.

La dérive génétique et la spéciation

Wright reconnaissait qu’en considérant uniquement la sélection, les organismes peuvent rester pris sur un pic, c’est-à-dire arrêter d’évoluer. Par exemple, on peut considérer cinq loci ABCDE / abcde, avec ABCDE représentant la combinaison ayant la meilleure valeur de fitness et abcde la deuxième. Chaque substitution à partir de ABCDE rendrait l’organisme moins « fit ». Donc, l’organisme restera pris sur ce pic, puisque tout changement diminuerait sa fitness. Par ailleurs, un organisme au génotype abcde n’aura pas de grandes chances d’évoluer en ABCDE puisqu’une substitution de a pour A et ainsi de suite causerait une valeur de fitness moindre. Wright appelle ce dilemme le peak shifting problem. Il misait beaucoup sur l’importance de la dérive génétique dans le processus de l’évolution pour cette raison.

C’est la dérive génétique, soit la modification aléatoire de la fréquence d’allèles dans une population, qui permet aux sous-populations de descendre du pic vers une vallée. Cela est possible dans de petites sous-populations puisque la dérive génétique aurait un effet puissant. Ensuite, la sélection naturelle va faire grimper la sous-population jusqu’au sommet du pic. Ce mouvement de sous-population vers un nouveau pic, soit le phénomène de peak-shift, représente la spéciation[6].

En optimisation évolutionniste

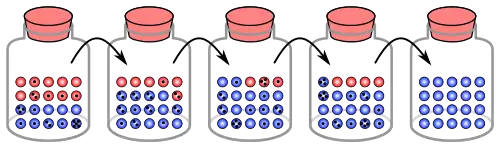
En dehors du domaine de la biologie évolutive, le concept de paysage de fitness a également gagné de l'importance dans les méthodes d'optimisation évolutive comme les algorithmes génétiques ou les stratégies évolutives. En optimisation évolutive, on essaie de résoudre des problèmes "du monde réel" (par exemple des problèmes d'ingénierie ou de logistique) en imitant la dynamique de l'évolution biologique. Par exemple, un camion de livraison avec un certain nombre d'adresses à livrer peut prendre une large variété de routes différentes, mais seulement une toute petite partie d'entre elles permettent d'avoir un temps de conduite relativement court.

Afin d'utiliser l'optimisation évolutive, on doit définir, pour chaque solution s possible (c'est-à-dire chaque route possible dans le cas du camion de livraison), à quel point elle est "bonne" par rapport au problème d'intérêt. Cela doit être fait en introduisant une fonction scalaire f(s) (scalaire signifiant que f(s) est un nombre simple, comme 0,3, alors que s peut être un objet plus compliqué, par exemple une liste d'adresses de livraison dans le cas du camion de livraison), qu'on appelle la fonction de fitness (fitness function en anglais).

Un f(s) élevé implique que s est une bonne solution. Dans le cas du camion de livraison, f(s) pourrait être le nombre de livraisons effectuées par heure en empruntant la route s. La meilleure solution, ou du moins une très bonne, est ensuite trouvée de la façon suivante : initialement, on crée une population de solutions aléatoires. Ensuite, les solutions sont mutées et on sélectionne celles ayant les fitness les plus fortes, jusqu'à ce qu'on ait trouvé une solution satisfaisante.

Les techniques d'optimisation évolutive sont particulièrement utiles dans des situations où il est facile de déterminer la qualité d'une seule solution, mais difficile de passer en revue toutes les solutions possibles une par une (il est facile de déterminer le temps de trajet du camion pour une route en particulier, mais il est presque impossible de vérifier toutes les routes possibles une fois que le nombre de destinations dépasse une simple poignée).

Le concept d'une fonction scalaire f(s) correspond aussi au concept d'une fonction d'énergie ou une fonction potentielle en physique. Les deux concepts diffèrent seulement dans le fait que les physiciens pensent traditionnellement en termes de minimisation de la fonction potentielle, alors que les biologistes préfèrent la notion selon laquelle la fitness est maximisée. Ainsi, prendre l'inverse d'une fonction potentielle revient à avoir une fonction de fitness, et vice-versa.

Critiques, mises en garde et limites

Relations dans le paysage

Si l’axe est phénotypique, le paysage ne reflète pas correctement l’évolution, puisque des organismes semblables phénotypiquement ne sont pas nécessairement proches évolutivement. En effet, le paysage adaptatif laisserait croire que les pics représentant des espèces qui sont à proximité l’un de l’autre seraient proches évolutivement[12].

La notion de fitness est variable

Le paysage adaptatif implique que le fitness d’un phénotype particulier est indépendant des autres organismes. Par contre, il faut tenir en compte que la sélection dépend fortement des interactions entre les organismes (ex : coadaptation). La hauteur du paysage en un point dépend alors de la distribution des autres points en ce même moment. De plus, les pics de fitness doivent être dynamiques, puisqu’ils changent nécessairement en fonction de l’environnement[12].

Nombre de dimensions

Comme l'esprit humain doit lutter pour conceptualiser au-delà de trois dimensions, les topologies en 3D peuvent induire en erreur quand on étudie des paysages de fitness multi-dimensionnels[5],[13]. En particulier, il n'est pas clair si les pics dans les paysages adaptatifs biologiques naturels sont vraiment séparés par des vallées de fitness dans de tels paysages multi-dimensionnels, ou bien s'ils sont connectés par des arêtes longues et neutres[14],[15].De plus, le paysage adaptatif n'est pas statique dans le temps mais dépend des changements environnementaux et de l'évolution d'autres gènes[9]. Il est donc plus proche d'un paysage marin[16], affectant par la suite la façon dont les pics adaptatifs peuvent vraiment être séparés. Enfin, comme il est commun d'utiliser la fonction comme un proxy pour la fitness lorsqu'on étudie les enzymes, toutes les activités de promiscuité existent en tant que paysages qui se chevauchent et qui, ensemble, déterminent la fitness finale de l'organisme.

Tout système biologique implique un nombre impensable de dimensions. En effet, selon Wright, le nombre de substitutions nécessaires pour bouger d’un génotype à l’autre pourrait être représenté par une certaine distance. Afin de bien représenter ces distances, il faudrait un nombre de dimensions égal au nombre de substitutions individuelles. Par exemple, pour 1000 loci avec 10 allèles chacun, il faudrait 9000 dimensions. Vu qu’il est impossible de représenter un tel nombre de dimensions, Wright a suggéré de « compresser » les dimensions et de simplement visualiser un paysage en 3D. Quoique ce ne serait pas une représentation mathématique adéquate, il stipule que ce serait suffisant pour comprendre les aspects important du processus évolutif[9]. En pratique, un espace multi-dimensionnel peut être réduit grâce à un traitement mathématique comme l'analyse en composantes principales ou d'autres techniques de la statistique multivariée.

Conclusion

Avec ces limites en tête, les paysages de fitness peuvent malgré tout être une façon instructive de penser l'évolution. Il est fondamentalement possible de mesurer (même sans pouvoir le visualiser) certains paramètres de robustesse du paysage et le nombre de pics, la hauteur, la séparation, et le regroupement. Des paysages en 3D simplifiés peuvent ensuite être utilisés les uns par rapport aux autres afin de représenter visuellement les caractéristiques pertinentes. De plus, les paysages de fitness de petits sous-groupes de voies évolutives peuvent être construits et visualisés expérimentalement, ce qui révèle potentiellement des caractéristiques telles que les pics de fitness et les vallées[9]. Les paysages de fitness de voies évolutives indiquent les étapes évolutives probables et les extrémités parmi des groupes de mutations individuelles.

Autres types de paysages

Paysage adaptatif à pic unique

Ce modèle, inspiré par Fisher implique que la sélection naturelle peut diriger la population vers un pic global sans avoir recours à la dérive génétique ni tout autre facteur. Selon Fisher, il y aurait donc qu’une seule combinaison parfaite de gènes. De plus, cette combinaison de gène peut être organisé par la sélection seule[17].

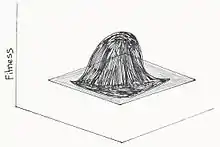
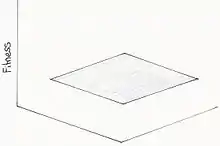
Paysage adaptatif plat

Ce modèle s'appuie sur la théorie neutre selon laquelle la plupart des changements évolutionnaire sont neutres au niveau moléculaire et donc ne change pas le fitness. Cette théorie introduit la possibilité de divergence génétique importante par des facteurs stochastiques en absence des forces de sélection. Vu qu’il n’y aurait pas de disparité entre la fitness des espèces, le paysage est plat[17].

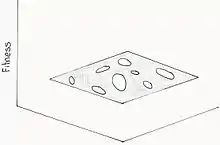
Paysage adaptatif troué

Ce modèle est fondé sur l’idée que le nombre de génotypes qu’il est possible de créer par simple substitution des paires de bases est infiniment plus grand que le nombre d’organismes à n’importe quel moment donné. Vu la redondance dans la carte génotype-fitness, différents génotypes ont nécessairement des fitness très similaires. Il y a donc une possibilité que les génotypes ayant un bon fitness forment des amas qui peuvent s’étendre à travers l’espace génotypique, soit l’ensemble de tous les génotypes possibles représenté par le paysage. Les populations pourraient alors évoluer à travers ces amas par simples substitutions, sans avoir à passer par des « vallées ». Les trous dans le paysage représentent les génotypes ayant un moins bon fitness[17]

Voir aussi

Notes

Articles connexes

Références
  1. Thomas Lenormand, Nicolas Rode, Luis-Miguel Chevin et François Rousset, « Chapitre 15 : Valeur sélective : définitions, enjeux et mesures », dans Frédéric Thomas, Michel Raymond et Thierry Lefèvre (dir.), Biologie évolutive, Louvain-la-Neuve, De Boeck Supérieur, , 2e éd. (1re éd. 2010), xxiv + 965 [détail de l’édition] (ISBN 978-2-8073-0296-9, présentation en ligne), p. 655-675.
  2. (en) Deirdre Barrett, Supernormal Stimuli : How primal urges overran their evolutionary purpose, États-Unis, W. W. Norton & Company, , 224 p. (ISBN 978-0-393-06848-1, lire en ligne)
  3. (en) S. Wright, Proceedings of the Sixth International Congress on Genetics, , 355–366 p. (lire en ligne), « The roles of mutation, inbreeding, crossbreeding, and selection in evolution »
  4. (en) Robert A., Jr. Skipper, « The Heuristic Role of Sewall Wright’s 1932 Adaptive Landscape Diagram », Philosophy of Science, vol. 71, no 5,‎ , p. 1176–1188 (ISSN 0031-8248, DOI 10.1086/425240, résumé)
  5. (en) David M. McCandlish, « Visualizing fitness landscapes », Evolution; International Journal of Organic Evolution, vol. 65, no 6,‎ , p. 1544–1558 (ISSN 0014-3820, PMID 21644947, PMCID PMC3668694, DOI 10.1111/j.1558-5646.2011.01236.x, lire en ligne)
  6. (en) Jonathan Michael Kaplan, Adaptive landscapes : Concepts, tools and metaphors (Reviewing E.I. Svensson and R. Calsbeek (Eds.), The adaptive landscape in evolutionary biology), Studies in History and Philosophy of Biological and Biomedical Sciences 44 :613-616, 2013, 792 p.
  7. Isabelle Olivieri, Renaud Vitalis et Pierre Henri Gouyon, « Chapitre 17 : Génétique et évolution des populations et des métapopulations », dans Frédéric Thomas, Michel Raymond et Thierry Lefèvre (dir.), Biologie évolutive, Louvain-la-Neuve, De Boeck Supérieur, , 2e éd. (1re éd. 2010), xxiv + 965 [détail de l’édition] (ISBN 978-2-8073-0296-9, présentation en ligne), p. 709-738.
  8. (en) Sergey Gavrilets, Evolution and speciation on holey adaptive landscapes, Trends in Ecology and Evolution, no.8, 12 : 307-312, 1997
  9. (en) Barrett Steinberg et Marc Ostermeier, « Environmental changes bridge evolutionary valleys », Science Advances, vol. 2, no 1,‎ , e1500921 (ISSN 2375-2548, PMID 26844293, PMCID PMC4737206, DOI 10.1126/sciadv.1500921, lire en ligne, consulté le )
  10. (en) William B. Provine, Sewall Wright and Evolutionary Biology, University of Chicago Press, , 561 p. (ISBN 978-0-226-68473-4, lire en ligne)
  11. (en) Jerry A. Coyne, Nicholas H. Barton, Michael Turelli, Perspective: a critique of Sewall Wright's shifting balance theory of evolution, Evolution no3, 51: 643–671, 1997, 1025 p. DOI:10.1111/j.1558-5646.1997.tb03650.x
  12. (en) Jon F. Wilkins et Peter Godfrey-Smith, Adaptationism and the adaptive landscape, Biology and Philosophy 24 : 199-214, 2009, 738 p.
  13. (en) Massimo Pigliucci, « Adaptive Landscapes, Phenotypic Space, and the Power of Metaphors », The Quarterly Review of Biology, vol. 83, no 3,‎ , p. 283–287 (ISSN 0033-5770, DOI 10.1086/590511, lire en ligne, consulté le )
  14. (en) Sergey Gavrilets, Fitness Landscapes and the Origin of Species, Princeton, New Jersey, États-Unis, Princeton University Press, , 476 p. (ISBN 0-691-11758-6, lire en ligne)
  15. (en) Jonathan Kaplan, « The end of the adaptive landscape metaphor? », Biology & Philosophy, vol. 23, no 5,‎ , p. 625–638 (ISSN 0169-3867 et 1572-8404, DOI 10.1007/s10539-008-9116-z, lire en ligne, consulté le )
  16. (en) Ville Mustonen et Michael Lässig, « From fitness landscapes to seascapes: non-equilibrium dynamics of selection and adaptation », Trends in genetics: TIG, vol. 25, no 3,‎ , p. 111–119 (ISSN 0168-9525, PMID 19232770, DOI 10.1016/j.tig.2009.01.002, lire en ligne, consulté le )
  17. (en) Sergey Gavrilets, Encyclopedia of Ecology : Fitness Lanscapes, Elsevier, 2008 :1612-1615, 4121 p. DOI:10.1016/B978-008045405-4.00804-1

Bibliographie
  • (en) Jerry A. Coyne, Nicholas H. Barton, Michael Turelli, Perspective: a critique of Sewall Wright's shifting balance theory of evolution, Evolution no3, 51: 643–671, 1997, 1025 p.
  • (en) Jon F. Wilkins et Peter Godfrey-Smith, Adaptationism and the adaptive landscape, Biology and Philosophy 24 : 199-214, 2009, 738 p.
  • (en) Jonathan Michael Kaplan, Adaptive landscapes : Concepts, tools and metaphors (Reviewing E.I. Svensson and R. Calsbeek (Eds.), The adaptive landscape in evolutionary biology), Studies in History and Philosophy of Biological and Biomedical Sciences 44 :613-616, 2013, 792 p.
  • (en) Sergey Gavrilets, Encyclopedia of Ecology : Fitness Lanscapes, Elsevier, 2008 :1612-1615, 4121 p.
  • (en) Sergey Gavrilets, Evolution and speciation on holey adaptive landscapes, Trends in Ecology and Evolution, no.8, 12 : 307-312, 1997
  • Portail origine et évolution du vivant
  • Portail de la biologie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.