Polynôme de Bernoulli

En mathématiques, les polynômes de Bernoulli apparaissent dans l'étude de beaucoup de fonctions spéciales et en particulier, la fonction zêta de Riemann ; des polynômes analogues, correspondant à une fonction génératrice voisine, sont connus sous le nom de polynômes d'Euler.

Polynômes de Bernoulli

Définition

Les polynômes de Bernoulli sont l'unique suite de polynômes $\left(B_{n}\right)_{n\in \mathbb {N} }$ telle que :

$B_{0}=1$
$\forall n\in \mathbb {N} ,B'_{n+1}=(n+1)B_{n}$
$\forall n\in \mathbb {N} ^{*},\int _{0}^{1}B_{n}(x)dx=0$

Fonctions génératrices

La fonction génératrice pour les polynômes de Bernoulli est

{\frac {te^{xt}}{e^{t}-1}}=\sum _{n=0}^{\infty }B_{n}(x){\frac {t^{n}}{n!}}

.

La fonction génératrice pour les polynômes d'Euler est

{\frac {2e^{xt}}{e^{t}+1}}=\sum _{n=0}^{\infty }E_{n}(x){\frac {t^{n}}{n!}}

.

Les nombres d'Euler et de Bernoulli

Les nombres de Bernoulli sont donnés par $B_{n}=B_{n}(0)$ .

Les nombres d'Euler sont donnés par $E_{n}=2^{n}E_{n}(1/2)$ .

Expressions explicites pour les petits ordres

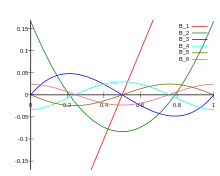
Les premiers polynômes de Bernoulli sont :

B_{0}(x)=1\,

B_{1}(x)=x-{\frac {1}{2}}

B_{2}(x)=x^{2}-x+{\frac {1}{6}}

B_{3}(x)=x^{3}-{\frac {3}{2}}x^{2}+{\frac {1}{2}}x

B_{4}(x)=x^{4}-2x^{3}+x^{2}-{\frac {1}{30}}

B_{5}(x)=x^{5}-{\frac {5}{2}}x^{4}+{\frac {5}{3}}x^{3}-{\frac {1}{6}}x

B_{6}(x)=x^{6}-3x^{5}+{\frac {5}{2}}x^{4}-{\frac {1}{2}}x^{2}+{\frac {1}{42}}

Les quelques premiers polynômes d'Euler sont :

E_{0}(x)=1\,

E_{1}(x)=x-{\frac {1}{2}}\,

E_{2}(x)=x^{2}-x\,

E_{3}(x)=x^{3}-{\frac {3}{2}}x^{2}+{\frac {1}{4}}\,

E_{4}(x)=x^{4}-2x^{3}+x\,

E_{5}(x)=x^{5}-{\frac {5}{2}}x^{4}+{\frac {5}{2}}x^{2}-{\frac {1}{2}}\,

E_{6}(x)=x^{6}-3x^{5}+5x^{3}-3x\,

Propriétés des polynômes de Bernoulli

Différences

Les polynômes de Bernoulli et d'Euler obéissent à beaucoup de relations du calcul ombral utilisé par Édouard Lucas, par exemple.

B_{n}(x+1)-B_{n}(x)=nx^{n-1}\,

E_{n}(x+1)+E_{n}(x)=2x^{n}\,

Dérivées

B_{n}'(x)=nB_{n-1}(x)\,

E_{n}'(x)=nE_{n-1}(x)\,

Translations

B_{n}(x+y)=\sum _{k=0}^{n}{n \choose k}B_{k}(x)y^{n-k}

E_{n}(x+y)=\sum _{k=0}^{n}{n \choose k}E_{k}(x)y^{n-k}

Symétries

B_{n}(1-x)=(-1)^{n}B_{n}(x)

E_{n}(1-x)=(-1)^{n}E_{n}(x)

(-1)^{n}B_{n}(-x)=B_{n}(x)+nx^{n-1}

(-1)^{n}E_{n}(-x)=-E_{n}(x)+2x^{n}

Autres propriétés

\forall n\in \mathbb {N} ,B_{n}(x)=2^{n-1}\left(B_{n}\left({\frac {x}{2}}\right)+B_{n}\left({\frac {x+1}{2}}\right)\right)

\forall p\in \mathbb {N} ,\forall n\in \mathbb {N} ,\sum _{k=0}^{n}k^{p}={\frac {B_{p+1}(n+1)-B_{p+1}(0)}{p+1}}

Cette dernière égalité, déduite de la formule de Faulhaber, vient de l'égalité : $\int _{x}^{x+1}B_{n}(t)\,\mathrm {d} t=x^{n}$ ou, plus simplement, de la somme télescopique

\sum _{k=0}^{n}\left(B_{m}(k+1)-B_{m}(k)\right)=B_{m}(n+1)-B_{m}(0)

.

Valeurs particulières

Les nombres $B_{n}=B_{n}(0)$ sont les nombres de Bernoulli.

\forall n>1,\quad B_{n}(0)=B_{n}(1)

Les nombres de Bernoulli de rang impair différent de 1 sont nuls :

\forall p\in \mathbb {N} ^{*}\quad B_{2p+1}(0)=B_{2p+1}(1)=0

\forall p\in \mathbb {N} \quad B_{2p+1}\left({\frac {1}{2}}\right)=0

\forall p\in \mathbb {N} \quad B_{2p}\left({\frac {1}{2}}\right)=\left({\frac {1}{2^{2p-1}}}-1\right)B_{2p}

Série de Fourier

La série de Fourier des polynômes de Bernoulli est aussi une série de Dirichlet, donnée par le développement[1] :

B_{n}(x)=-{\frac {n!}{(2\pi \mathrm {i} )^{n}}}\sum _{k\in \mathbb {Z}  \atop k\neq 0}{\frac {\mathrm {e} ^{2\pi \mathrm {i} kx}}{k^{n}}}=-n!\sum _{k=1}^{\infty }{\frac {\mathrm {e} ^{2\pi \mathrm {i} kx}+(-1)^{n}\mathrm {e} ^{-2\pi \mathrm {i} kx}}{(2\pi \mathrm {i} k)^{n}}}=-2\,n!\sum _{k=1}^{\infty }{\frac {\cos \left(2k\pi x-{\frac {n\pi }{2}}\right)}{(2k\pi )^{n}}}

,

valide seulement pour 0 ≤ x ≤ 1 lorsque n ≥ 2 et pour 0 < x < 1 lorsque n = 1.

C'est un cas particulier de la formule de Hurwitz.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bernoulli polynomials » (voir la liste des auteurs).

(en) Tsuneo Arakawa, Tomoyoshi Ibukiyama et Masanobu Kaneko, Bernoulli Numbers and Zeta Functions, Springer, 2014 (lire en ligne), p. 61.

Voir aussi

Bibliographie

(en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne), chap. 23
(en) Tom M. Apostol, Introduction to Analytic Number Theory, 1976, Springer-Verlag, New York, chap. 12.11

Articles connexes

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Tsuneo Arakawa, Tomoyoshi Ibukiyama et Masanobu Kaneko, Bernoulli Numbers and Zeta Functions, Springer, 2014 (lire en ligne), p. 61.