Polytrope

Le terme de polytrope désigne une forme de matière dont l'équation d'état ne dépend que de deux paramètres, la masse volumique μ et la pression P, reliées l'une à l'autre par la relation[1]^,[2]

${\displaystyle P=\kappa \mu ^{\gamma }}$,

où κ est une constante arbitraire positive et γ un nombre appelé indice adiabatique. En pratique on préfère utiliser une quantité dérivée, l'indice polytropique n défini par

${\displaystyle \gamma =1+{\frac {1}{n}}}$.

On a montré que pour une polytrope, l'indice adiabatique est égale à la dérivée de la pression du module d'élasticité[3] et sa relation avec l'équation d'état de Murnaghan a aussi été démontrée.

Un polytrope est un cas particulier de barotrope. Plusieurs formes de matière réalistes correspondent à différentes valeurs de l'indice polytropique. En particulier :

• Un gaz parfait isotherme correspond à ${\displaystyle \gamma =1}$, soit ${\displaystyle n=\infty }$. Ceci est une conséquence directe de l'équation d'état des gaz parfaits, en prenant la température constante.
• De la matière dégénérée, c'est-à-dire suffisamment dense pour que les effets quantiques dus au principe d'exclusion de Pauli se fasse sentir, a un indice polytropique de 3/2 (γ = 5/3) si elle est non relativiste et de 3 (γ = 4/3) si elle est relativiste.
• Un milieu incompressible est de densité constante quelle que soit la pression. En inversant la relation fondamentale, on a ${\displaystyle \mu \propto P^{\frac {1}{\gamma }}}$. Pour que la densité soit indépendante de la pression, il faut que l'exposant 1/γ soit nul, soit γ infini, c'est-à-dire n nul.

En thermodynamique, on associe à un polytrope le concept de transformation polytropique, en particulier pour un gaz parfait, au sens d'une transformation durant laquelle la pression et la densité sont reliées par une relation du type ci-dessus.

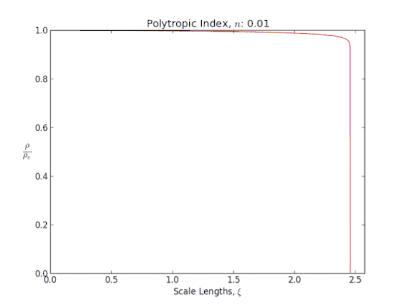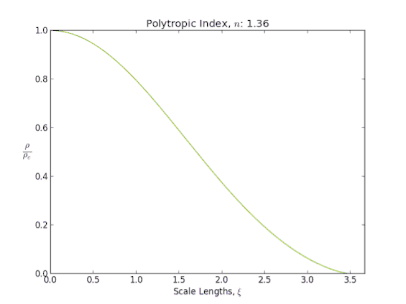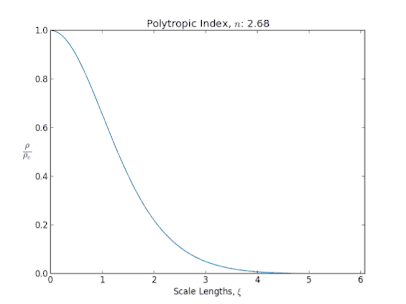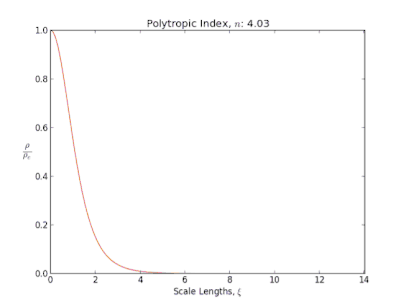
Ce type de fluide joue un rôle important en astrophysique où il permet de modéliser la structure interne de plusieurs objets célestes très divers. Dans ce contexte est étudiée la structure d'un fluide polytropique autogravitant, c'est-à-dire soumis à son propre champ de gravité. L'équation fondamentale qui décrit ces objets est alors appelée équation de Lane-Emden. En particulier, elle révèle qu'un changement radical de structure d'un objet se produit dans certaines situations quand sa masse dépasse une certaine valeur critique et que son indice polytropique atteint la valeur de 3. Ce point joue un rôle crucial dans deux situations :

• Une naine blanche dont la masse dépasse une valeur critique appelée masse de Chandrasekhar va subir une instabilité qui va engendrer une réaction de fusion thermonucléaire sur l'ensemble de l'astre, provoquant ainsi sa dislocation. Ce phénomène, appelé supernova thermonucléaire est extraordinairement lumineux, permettant à l'astre de rayonner pendant quelques jours autant qu'une galaxie tout entière, devenant visible à plusieurs milliards d'années-lumière de distance.
• Une étoile massive dont le cœur, composé de fer atteint la même masse critique, va voir celui-ci imploser, générant après coup une onde de choc qui disloque l'ensemble des couches externes de l'étoile. On parle alors de supernova à effondrement de cœur, phénomène plus énergétique, mais en général légèrement moins lumineux que les supernovae thermonucléaires.

• Indice polytropique
• Barotrope
• Sphère isotherme
• Équation de Lane-Emden
• Transformation polytropique

• Portail de l’astronomie