Projection équivalente cylindrique de Lambert
En cartographie, la projection équivalente cylindrique de Lambert, ou projection cylindrique de Lambert, ou encore projection isocylindrique [1] est un type de projection cartographique. Elle fait partie de la famille des projections cylindriques équivalentes. Cette projection est sans distorsion le long de l'équateur, qui est son parallèle de base, mais la distorsion croît rapidement à l'approche des pôles. Comme pour toute projection cylindrique, les parallèles sont de plus en plus étirés en s'éloignant de l'équateur. Les pôles correspondent à une distorsion infinie, les deux points extrêmes étant étirés en des segments de droites.
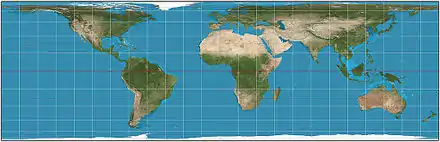


Historique
La projection est attribuée au mathématicien alsacien Johann Heinrich Lambert en 1772[2].
Dans l'ouvrage De la sphère et du cylindre, Archimède a montré qu'une sphère a la même aire que le cylindre qui l'entoure (si on ne considère pas les deux faces circulaires), et bien qu'Archimède ne discute pas la projection explicitement, cet argument montre que la projection préserve les aires.
Références
- Yann Ollivier, « Les projections cylindriques »
- Karen Mulcahy, « Cylindrical Projections », City University of New York (consulté le )
- Map Projections – A Working Manual, USGS Professional Paper 1395, John P. Snyder, 1987, pp. 76–85
Voir aussi
Articles connexes
Liens externes
- (en) Table of examples and properties of all common projections, from radicalcartography.net
- (en) An interactive Java Applet to study the metric deformations of the Lambert Cylindrical Equal-Area Projection.
- Portail de la géodésie et de la géophysique
- Portail de l’astronomie
- Portail de la cartographie