Règle du parallélogramme

En mathématiques, la forme la plus simple de la règle du parallélogramme (ou identité du parallélogramme, ou encore égalité du parallélogramme) est celle de géométrie élémentaire. Elle dit que la somme des carrés des longueurs des quatre côtés d'un parallélogramme est égale à la somme des carrés des longueurs de ses deux diagonales : $AB^{2}+BC^{2}+CD^{2}+DA^{2}=AC^{2}+BD^{2}$

Les vecteurs x + y et x – y forment les diagonales du parallélogramme de côtés x et y.

ou encore, puisque deux côtés opposés ont même longueur :

2AB^{2}+2BC^{2}=AC^{2}+BD^{2}.

(Dans le cas où le parallélogramme est un rectangle, les diagonales sont de longueurs égales, ce qui ramène cette règle au théorème de Pythagore.)

Formulation vectorielle

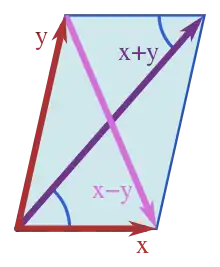
Tout espace affine dont l'espace vectoriel associé est muni d'une norme hérite de ce fait d'une distance. La règle ci-dessus, sur les distances dans un parallélogramme, se traduit sur la norme par l'identité suivante, pour tous vecteurs x et y :

$2\|x\|^{2}+2\|y\|^{2}=\|x+y\|^{2}+\|x-y\|^{2}.$

La règle du parallélogramme dans les espaces préhilbertiens

L'identité ci-dessus est valide dans les espaces préhilbertiens (en particulier les espaces de Hilbert), où la norme est définie à partir du produit scalaire par $\|x\|^{2}=\langle x,x\rangle .$

Espaces normés satisfaisant la règle du parallélogramme

La formulation vectorielle ci-dessus a un sens dans tout espace vectoriel normé. Un fait remarquable[1] est que l'identité reste valide seulement si la norme se déduit d'un produit scalaire : c'est le théorème de Fréchet-von Neumann-Jordan (le produit scalaire qui génère cette norme est alors unique, d'après l'identité de polarisation).

Équivalence avec l'identité de la médiane

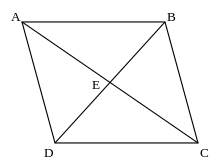
Une norme sur un espace vectoriel $V$ vérifie l'identité du parallélogramme si et seulement si elle vérifie l'identité de la médiane : pour tout triangle $ABC$ (dans un espace affine de direction $V$ ), en notant $E$ le milieu de [ $AC$ ] :

$AB^{2}+BC^{2}={\frac {1}{2}}AC^{2}+2BE^{2}.$

Cette équivalence résulte de l'égalité $BD = 2BE$ , où $D$ désigne le point tel que $ABCD$ soit un parallélogramme. Elle est tout aussi immédiate en comparant[2] la formulation vectorielle ci-dessus de l'identité du parallélogramme et la réécriture de celle de la médiane (avec $x={\overrightarrow {BA}}{\text{ et }}y={\overrightarrow {BC}}$ ) sous la forme

$\|x\|^{2}+\|y\|^{2}={\frac {1}{2}}\|x-y\|^{2}+2\left\|{\frac {x+y}{2}}\right\|^{2}.$

Identité du parallélogramme généralisée

Pour tout espace préhilbertien $H$ , on a, plus généralement[3] :

$\forall n\in \mathbb {N} ^{*}\quad \forall x_{1},\ldots ,x_{n}\in H\quad 2^{n}\sum _{i=1}^{n}\|x_{i}\|^{2}=\sum _{(\varepsilon _{1},\ldots ,\varepsilon _{n})\in \{-1,1\}^{n}}\left\|\sum _{i=1}^{n}\varepsilon _{i}x_{i}\right\|^{2}$

(en développant le membre de droite, petit à petit ou directement).

Cette identité permet de montrer que la distance de Banach-Mazur entre ℓ^p(n) et ℓ²(n) est égale à n^{|1/p – 1/2|}.

Notes et références

On peut de plus remarquer que (par changement de variables) l'identité est valide dès que l'inégalité large (dans un sens ou dans l'autre) l'est. Pour des conditions suffisantes encore plus faibles, voir « Identité de polarisation », § Cas réel ou (en) David Albert Senechalle, « A characterization of inner product spaces », Proc. Amer. Math. Soc., vol. 19,‎ 1968, p. 1306-1312 (lire en ligne).
J. Freslon et J. Poineau, Mathématiques : Les exercices incontournables PC-PSI-PT, Dunod, 2010 (ISBN 978-2-10-056032-5, lire en ligne), p. 59.
Cf. Hervé Queffélec et Claude Zuily, Analyse pour l'agrégation, Dunod, 2020, 5^e éd. (lire en ligne), p. 228 et 239 (ex. 11 et solution) ou cet exercice corrigé de la leçon « Espaces vectoriels normés » sur Wikiversité.

Articles connexes

Théorème de projection sur un convexe fermé, dont le présent théorème est un argument clé
Relation d'Euler dans le quadrilatère

Portail des mathématiques

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] On peut de plus remarquer que (par changement de variables) l'identité est valide dès que l'inégalité large (dans un sens ou dans l'autre) l'est. Pour des conditions suffisantes encore plus faibles, voir « Identité de polarisation », § Cas réel ou (en) David Albert Senechalle, « A characterization of inner product spaces », Proc. Amer. Math. Soc., vol. 19,‎ 1968, p. 1306-1312 (lire en ligne).

[2] J. Freslon et J. Poineau, Mathématiques : Les exercices incontournables PC-PSI-PT, Dunod, 2010 (ISBN 978-2-10-056032-5, lire en ligne), p. 59.

[3] Cf. Hervé Queffélec et Claude Zuily, Analyse pour l'agrégation, Dunod, 2020, 5^e éd. (lire en ligne), p. 228 et 239 (ex. 11 et solution) ou cet exercice corrigé de la leçon « Espaces vectoriels normés » sur Wikiversité.