Réaction nucléaire

Une réaction nucléaire est le processus au cours duquel un ou plusieurs noyaux atomiques sont transformés pour donner des noyaux de masse et/ou de charge différentes. Elle se distingue d'une réaction chimique, qui ne concerne que les électrons ou les liaisons entre les atomes. La réaction chimique conserve les éléments chimiques, alors que la réaction nucléaire transforme un nucléide en un autre.

Pour les articles homonymes, voir Réaction.

La plupart des réactions nucléaires impliquent l’interaction de deux noyaux ou particules ; certains processus comme la fission spontanée des noyaux lourds ou les radioactivités (alpha, beta et gamma) concernent des noyaux isolés. Le terme « réaction nucléaire » peut donc désigner soit une modification d'un nucléide induite par collision avec une autre particule, soit une modification spontanée d'un noyau sans collision.

Il existe une très grande variété de réactions nucléaires[1], qui sont soit des processus spontanés comme la désintégration radioactive du radium observée par Marie Curie, soit des processus provoqués, tels la fusion nucléaire à l’œuvre dans la nucléosynthèse stellaire, la fission de l’uranium dans les centrales électriques ou les collisions de noyaux dans les accélérateurs de particules[2].

Histoire des réactions nucléaires

La première observation d'une transformation d'un noyau atomique en un autre a été la découverte et l'étude de la radioactivité naturelle par Frederick Soddy et Ernest Rutherford, en 1903[3]. La première réaction nucléaire « artificielle » entre noyaux a été effectuée par Rutherford en 1919, en bombardant des noyaux d’azote par des particules alpha issues d’une source radioactive.

Les noyaux radioactifs sont des sources limitées en nucléides (neutrons, protons, noyaux d’hélium 4) et en énergie. Les avancées de la physique des réactions nucléaires allait aller de pair avec le développement des accélérateurs et des détecteurs (voir le chapitre V.5 de la référence[3]).

Dans un premier temps, les accélérateurs électrostatiques ont été utilisés avec une course vers les hautes tensions (foudre, bobine de Tesla, etc.). À partir de 1930, l'ingénieur Robert Van de Graaff construit des générateurs électrostatiques éponymes avec des tensions qui dépassent le million de volts (MeV). Une technologie alternative, basée sur les champs magnétiques est développée à partir de 1932, notamment par Ernest Lawrence à Berkeley qui met au point le premier cyclotron. À partir de là, notamment avec la technologie des aimants supraconducteurs, les performances des accélérateurs se sont considérablement améliorées, pour atteindre plusieurs millions de MeV (TeV) par nucléon.

Irène et Frédéric Joliot-Curie découvrent en 1934 la radioactivité artificielle : les réactions nucléaires provoquées par des noyaux accélérés peuvent produire de nouveaux noyaux radioactifs, inconnus dans la nature car de durée de vie très courte. C’est le début d’une exploration systématique de la carte des noyaux atomiques, notamment ceux trop instables pour exister naturellement et qui ne sont accessibles que par des réactions nucléaires provoquées en laboratoire (voir chapitre V.7 de la référence[3])

En 1938-1939, Hans Bethe et Carl Friedrich von Weizsäcker démontrent que l’énergie du Soleil, et donc l’énergie des étoiles, était le résultat d’une cascade de réactions nucléaires (cycle carbone-azote-oxygène) provoquant la fusion de l’hydrogène en hélium, avec production d’une grande quantité d’énergie.

En 1938, O. Hahn, L. Meitner et F. Strassman découvrent la fission des noyaux lourds comme l’uranium ; alors que les réactions nucléaires connues jusqu’alors produisaient des noyaux différents de quelques unités de masse et de charge des noyaux initiaux, la fission était le seul processus de réaction permettant, par exemple, la production de noyaux de baryum (56 protons et environ 80 neutrons) à partir de noyaux d'uranium (92 protons et 146 neutrons). La découverte par Frédéric Joliot-Curie de la possibilité d’induire la fission des noyaux d’uranium 235 par absorption de neutrons mettait les chercheurs sur la piste de la réaction en chaîne, qui allait conduire à la bombe A et à la production d’énergie dans les centrales nucléaires.

Les bombes nucléaires ont ensuite utilisé le principe de fusion de noyaux isotopes lourds de l'hydrogène (deutérium et tritium), menant aux bombes « à hydrogène » ou bombes H, beaucoup plus puissantes et destructrices.

Représentation

Une réaction nucléaire peut être représentée par une équation semblable à celle représentant une réaction chimique. Des désintégrations nucléaires peuvent être représentées d'une manière semblable, mais avec seulement un noyau à gauche.

Chaque particule est écrite avec son symbole chimique, avec son numéro atomique à gauche en bas, et son nombre de masse en haut. Pour le neutron, le symbole est n. Le proton peut être noté « H » (noyau d'hydrogène) ou « p ».

Pour vérifier l'équation, on doit contrôler que les sommes des nombres atomiques soient égales à gauche et à droite (à cause de la loi de conservation de la charge électrique), et que les sommes des nombres de masse soient aussi égales à gauche et à droite (à cause de la loi de conservation du nombre baryonique).

Par exemple :

6
3Li + 2
1H ⟶ 4
2He + 4
2He.

La première réaction nucléaire observée par Rutherford s'écrirait aujourd'hui :

4
2He + 14
7N ⟶ 17
8O + 1
1H

Une des voies possibles de la fission induite de l'uranium :

235
92U + 1
0n ⟶ 146
58Ce + 85
34Se + 5 1
0n

Représentation simplifiée

Des notations abrégées sont utilisées pour les nucléides ou particules qui apparaissent très souvent. Par exemple, le noyau 4He (qui s'appelle aussi particule alpha, dans un type de radioactivité) est abrégé avec la lettre grecque « α ». Les noyaux de deutérium (hydrogène lourd, 2H) sont dénotés simplement « D ».

Les nombres atomiques sont donnés implicitement par les symboles chimiques, ils peuvent être supprimés quand l'équation a été vérifiée. Par conséquent, on pourrait périphraser l'exemple précédent en introduisant des symboles :

6
3Li + D ⟶ α + α

puis, supprimant les nombres atomiques :

6Li + D ⟶ α + α

Beaucoup de réactions sont binaires, avec en entrée une particule légère impactant un noyau lourd, et en sortie deux noyaux ou particules différentes. Ces réaction sont notées : noyau initial (particule incidente, particule sortante) noyau final[1]

  • collision élastique : par exemple 28Si (p,p) 28Si
  • collision inélastique : 28Si (p,p') 28Si* ; l'astérisque note que le noyau sortant n'est plus dans son état fondamental
  • plus généralement, 12C(12C,α)20Ne décrit la réaction d'un faisceau de carbone sur une cible de carbone, qui produit une fusion partielle en un noyau de néon avec éjection d'une particule α.

Conservation de l'énergie

L'énergie est conservée dans toutes les réactions nucléaires, le bilan doit être effectué en tenant compte des lois de la relativité restreinte : l'équivalent masse - énergie (E=mc2) et la masse relativiste pour les particules ayant des vitesses proches de la lumière.

Lorsqu'il y a production d'énergie avec perte de masse, la réaction est exothermique ; lorsqu'il faut fournir de l'énergie (par exemple, l'énergie cinétique des particules accélérées du faisceau dans les accélérateurs), les réactions sont endothermiques.

Par exemple, pour la réaction :

6
3Li + 2
1H ⟶ 4
2He + 4
2He.

Une table[4] donne avec précision les masses au repos des particules et noyaux ; soit 6,015 unités de masse atomique (abrégé u) pour le noyau 6
3Li ; 2,014 u pour le deutéron ; 4,002 6 u pour le deutéron. Par conséquent :

  • masse totale au repos dans la voie d'entrée : 6,015 + 2,014 = 8,029 u ;
  • et dans la voie de sortie : 2 × 4,002 6 = 8,005 2 u ;
  • il y a une perte de masse de 8,029 - 8,005 2 = 0,023 8 u.

Cette masse est l'équivalent de l'énergie produite par la réaction exothermique soit 0,023 8 × 931 MeV = 22,4 MeV.

Equivalence masse-énergie

Dans le Système international d'unités, la vitesse de la lumière est déterminée, ainsi que l'unité de masse atomique unifiée qui est définie comme valant 1⁄12 de la masse du noyau de carbone, soit : 1,660 54 × 10−27 kg 1 u c2 = (1,660 54 × 10−27 kg) × (2,997 92 × 108 m/s)2 = 1,492 42 × 10−10 kg (m/s)2 = 1,492 42 × 10−10 J (joule) = 1,492 42 × 10−10 x 6,24 × 1018 eV = 931,5 MeV Par conséquent, 1 u.c2 = 931,5 MeV.

 

L'énergie libérée dans une réaction nucléaire peut apparaître en trois manières différentes :

En général, les noyaux produits sont différents de ceux d'entrée, ce qui conduit à des réarrangements de leurs couches électroniques, avec émission de rayons X (énergies de l'ordre de l'électronvolt, beaucoup plus faibles que celles en jeu dans les réactions nucléaires, voir Transition électronique).

Bilan d'énergie

En écrivant l'équation de réaction, d'une manière analogue à une équation chimique, on peut en plus donner l'énergie de réaction du côté droit :

Noyau cible + projectile → Noyau final + éjectile + Q

L'énergie de réaction (la « valeur Q ») est positive pour les réactions exothermiques et négative pour les réactions endothermiques, contrairement à l'expression similaire en chimie. On peut la calculer soit comme la différence entre les sommes des énergies cinétiques dans la voie de sortie et dans la voie d'entrée, soit comme la différence entre les masses nucléaires au repos dans la voie d'entrée et dans la voie de sortie.

La réaction précédente avec son bilan d'énergie s'écrit : 6
3Li + 2
1H ⟶ 4
2He + 4
2He + 22,4 MeV.

Typologie des réactions nucléaires

Le nombre de réactions nucléaires possibles est immense[1], augmenté encore par l'arrivée des accélérateurs de particules capables d'accélérer une large variété de noyaux, dans une très grande gamme d'énergie. Parmi les plus notables, on peut citer les suivantes.

Réactions de fusion-fission

Dans les réactions de fusion, deux noyaux légers se réunissent pour en former un plus lourd (noyau composé) avec des particules supplémentaires (généralement des protons ou des neutrons) émises par la suite.

Dans les réactions de fission, un noyau très lourd se divise en deux ou parfois trois fragments ; la fission peut être spontanée pour les noyaux les plus lourds, ou induite par absorption de particules légères (généralement des neutrons). La fission spontanée, qui se produit sans l'aide d'un neutron, n'est généralement pas considérée comme une réaction nucléaire.

Dans la radioactivité alpha, bien que déterminée par les mêmes forces sous-jacentes que la fission spontanée, est généralement considérée comme distincte de cette dernière.

L'émission gamma induite appartient à une classe dans laquelle seuls les photons sont impliqués dans la création et la désexcitation des états d'excitation nucléaire.

Réactions directes

Un projectile à énergie intermédiaire transfère de l'énergie ou capte ou perd des nucléons au noyau en un seul événement rapide (10−21 seconde). Le transfert d'énergie et de quantité de mouvement est relativement faible. Ceux-ci sont particulièrement utiles en physique nucléaire expérimentale, car les mécanismes de réaction sont souvent assez simples à calculer avec une précision suffisante pour sonder la structure du noyau cible.

Diffusions inélastiques

Dans les Diffusions inélastiques, seules l'énergie et la quantité de mouvement sont transférées :

  • (p,p') teste les différences entre les états nucléaires ;
  • (α,α') mesure les formes et les tailles des surfaces nucléaires. Étant donné que les particules qui frappent le noyau réagissent plus violemment, la diffusion élastique et inélastique peu profonde est sensible à la forme et à la taille des cibles ;
  • (e,e') est utile pour sonder la structure intérieure. Comme les électrons interagissent moins fortement que les protons et les neutrons, ils atteignent les centres des cibles et leurs fonctions d'onde sont moins déformées en traversant le noyau.

Réactions d'échange de charges

L'énergie et la charge sont transférées entre le projectile et la cible. Voici quelques exemples de ce type de réactions :

Réactions de transfert de nucléons

Habituellement, à une énergie modérément basse, un ou plusieurs nucléons sont transférés entre le projectile et la cible. Ceux-ci sont utiles pour étudier la structure de l'enveloppe externe des noyaux. Des réactions de transfert peuvent se produire, du projectile vers la cible (en anglais stripping), ou de la cible au projectile (en anglais pick-up) :

  • (α,n) et (α,p) réactions. Certaines des premières réactions nucléaires étudiées impliquaient une particule alpha produite par désintégration alpha, faisant tomber un nucléon d'un noyau cible ;
  • réactions (d,n) et (d,p). Un faisceau de deutérons heurte une cible ; les noyaux cibles absorbent soit le neutron, soit le proton du deutéron. Le deutéron est si faiblement lié que c'est presque la même chose que la capture de protons ou de neutrons. Un noyau composé peut se former, entraînant une émission plus lente de neutrons supplémentaires. Les réactions (d,n) sont utilisées pour générer des neutrons énergétiques ;
  • la réaction d'échange d'étrangeté (K, π) a été utilisée pour étudier les hypernoyaux.

Réactions nucléaires dans les étoiles

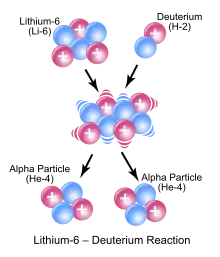
Si l'on exclut celles provoquées en laboratoire, les principales réactions nucléaires se produisent dans le cœur des étoiles. Les conditions extrêmes de pression et de température donnent aux noyaux l'énergie cinétique nécessaire pour passer la barrière coulombienne qui les séparent ; ces multiples réactions nucléaires sont la source de l'énergie de rayonnement des étoiles et de la création de noyaux de plus en plus lourds.

La réaction précédemment discutée intervient dans la fusion de l'hélium ; le 6Li et le deutérium réagissent en formant un noyau atomique intermédiaire, très excité, de 8Be, qui se désintègre très vite en produisant deux particules alpha. La figure suivante illustre cette réaction, les protons sont représentés par des sphères rouges, et les neutrons, par des sphères bleues.

En transformant une fraction de sa masse selon ce processus, le Soleil entretient ainsi sa propre production d'énergie, ce qui lui permettra encore de briller pendant plus de 10 milliards d'années[réf. nécessaire].

Taux de réaction

Le nombre de réactions par unité de temps dans un volume est donné par : où :

  •  : flux (différentiel) de particules incidentes en compris entre les énergies et
  •  : section efficace macroscopique de la cible en pour une particule incidente d'énergie

Dans le cas où le flux et la section efficace macroscopique sont uniformes dans le volume V, il est alors possible de simplifier l'équation ci-dessus de la façon suivante :

Voir aussi

Articles connexes

Liens externes

Références
  1. (en) Herman Feshbach, Theoretical nuclear physics : nuclear reactions, Wiley, (ISBN 0-471-05750-9, 978-0-471-05750-5 et 0-471-57796-0, OCLC 23219184).
  2. Luc Valentin, Le monde subatomique : des quarks aux centrales nucléaires, Hermann, (ISBN 2-7056-6043-7 et 978-2-7056-6043-7, OCLC 300428165).
  3. Bernard Fernandez (Ouvrage de référence pour l'ensemble de la section), De l'atome au noyau : une approche historique de la physique atomique et de la physique nucléaire, Ellipses, (ISBN 2-7298-2784-6 et 978-2-7298-2784-7, OCLC 69665126).
  4. (en) Atomic Weights and Isotopic Compositions with Relative Atomic Masses, NIST.
  • Portail de la physique
  • Portail du nucléaire
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.