Réflectivité bidirectionnelle
Dans de nombreux problèmes de transferts thermiques[1],[2] ou en rendu pour la génération d'images de synthèse[3] il est nécessaire de caractériser la réflexion d'une surface. Le cas le plus simple est la réflexion spéculaire décrite par les lois de Fresnel mais qui ne s'adresse qu'à des surfaces parfaites. De telles surfaces sont réalisées dans divers domaines technologiques et on peut dans ce cas prédire, outre la réflexion, des propriétés telles que absorptivité ou émissivité. Pour les surfaces complexes (inhomogènes, rugueuses, partiellement transparentes, etc.) rencontrées dans la vie courante les méthodes physiques permettant d'accéder aux propriétés sont inefficaces à cause de la complexité de tels problèmes.
Les propriétés de réflexion sont entièrement contenues dans la relation qui relie la luminance incidente et la luminance réfléchie pour la fréquence qui nous intéresse. Dans ces expressions chaque direction est définie par les angles et qui sont les angles de colatitude (ou angle zénithal) et d'azimut (ou longitude) .
Pour établir cette relation il faut connaître la fonction de distribution probabiliste pour un photon incident d'être réfléchi dans l'angle solide autour de . Cette distribution caractérise la réflectivité bidirectionnelle et s'exprime en sr-1. Elle est souvent désignée par son acronyme anglais BRDF (Bidirectional Reflectance Distribution Function). Elle n'est pas normalisée (elle ne conserve pas l'énergie) pour prendre en compte l'absorption.
Le calcul de cette quantité à partir de la description géométrique et des propriétés du matériau n'est que rarement utilisé en raison de sa complexité. On se base généralement sur la mesure par un appareil spécifique. Toutefois le résultat brut n'est guère utilisable en l'état en raison de la quantité de données, en particulier pour les problèmes d'infographie. Pour cette raison de nombreuses lois approximatives ont été élaborées.
Définitions, propriétés

Luminance
Pour caractériser le transfert radiatif on utilise la luminance énergétique (ou densité spectrale de luminance énergétique), en J⋅m-2⋅sr-1, définie comme la quantité d'énergie radiative émise dans un intervalle de fréquence , dans un angle solide , traversant l'aire élémentaire durant le temps
Luminance sortante
On suppose que le matériau est suffisamment opaque pour que l'on puisse ignorer
- une éventuelle partie transmise à travers le matériau ;
- un décalage spatial notable entre le point d'arrivée du photon incident et celui du photon réémis.
La luminance sortante est donnée par le produit de convolution reliant tous les rayons incidents autour de la direction qui génèrent un rayon sortant dans la direction
Propriétés de la BRDF
- C'est une probabilité donc
- Réciprocité (théorème de réciprocité de Lorentz basé sur la linéarité des phénomènes physiques mis en jeu) : principe que l'on peut illustrer par la formule "si, après n'importe quel cheminement de la lumière, je peux vous voir, alors vous pouvez me voir".
- Conservation de l'énergie : le flux (exitance) réémis est inférieur ou égal au flux incident (il peut y avoir une absorption)
À propos de la géométrie du problème
- Si le problème est de révolution autour de la normale à la surface il n'y a plus de dépendance en et séparément mais seulement en , ce qui fait passer de 4 à 3 le nombre de variables.
- La présence d'une réflexion spéculaire gêne considérablement la représentation dans la mesure où il est difficile de capturer numériquement un lobe étroit. D'où l'idée d'effectuer une rotation des axes dans lesquels on représente la BRDF pour chaque rayon incident de façon à renvoyer le rayon réfléchi éventuel vers une région dédiée à une description détaillée[4].
Modèles de BRDF

Les BRDF sont obtenues par mesure sur un appareil doté d'un goniomètre ayant généralement une source de type lampe à décharge et un monochromateur permettant de générer des données à diverses longueurs d'onde, trois au moins si l'on veut générer une image en couleurs. La quantité de données est considérable et ne peut être utilisée directement. Il faut donc trouver une approximation de la distribution angulaire du rayonnement pour chaque incidence d'émission. Diverses approches sont possibles[5] :
- une approche purement mathématique consistant à décomposer la distribution expérimentale sur une base polynomiale : harmoniques sphériques, polynômes de Zernike projetés sur un hémisphère, ondelettes bidimensionnelles. Il faut utiliser un nombre de polynômes élevé pour obtenir une précision raisonnable, particulièrement dans le cas où des zones d'émission étroites sont présentes.
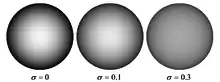
- une approche proche de la précédente mais dans laquelle le choix de l'ensemble sur lequel repose l'approximation est empirique. Un exemple simple est la superposition d'un terme isotrope avec un terme concentré dans la direction de réflexion spéculaire , par exemple du type et qui produit un lobe d'autant plus étroit que est grand. Un exemple classique est le modèle de Phong
- une approche basée sur des modèles physiques élémentaires, par exemple une surface représentée par des facettes d'orientation aléatoire, dotées d'une réflexion spéculaire ou au contraire parfaitement diffuse (générant un rayonnement isotrope localement). On peut régler comme on le souhaite la distribution statistique d'orientation des facettes liée à la rugosité de la surface. Les exemples les plus classiques sont le modèle de Torrance-Sparrow (de) pour la réflexion spéculaire et le modèle de Oren–Nayar (en) pour la réflexion diffuse.
Références
- (en) Michael M. Modest, Radiative Heat Transfer, Academic Press, 2003 (ISBN 0-12-503163-7)
- (en) John R. Howell, M. Pinar Menguç, Robert Siegel, Thermal Radiation Heat Transfer, CRC Press, 2010 (ISBN 1-43-980533-4)
- (en) Jeffrey J. McConnell, Anthony Ralston, Edwin D. Reilly, David Hemmendinger, Computer Graphics Companion, Wiley, 2002 (ISBN 978-0-470-86516-3)
- (en) Szymon M. Rusinkiewicz, A New Change of Variables for Efficient BRDF Representation, Eurographics Workshop on Rendering , 1998
- (en) Rosana Montes, Carlos Ureña, An Overview of BRDF Models, Technical Report LSI-2012-001, Université de Grenade, 2012
Articles connexes
Liens externes
- Portail de la physique
- Portail de l’optique
- Portail de l’imagerie numérique