Réseau de Halbach
Un réseau de Halbach est une disposition particulière d'aimants permanents qui accroît le champ magnétique d'un côté tout en éliminant presque totalement le champ magnétique de l'autre côté[1],[2]. Ceci est obtenu en faisant tourner les orientations des champs magnétiques sur les aimants successifs.
.png.webp)
.png.webp)
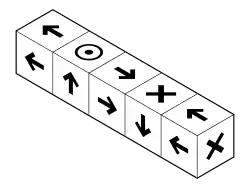
La disposition des aimants permanents (sur la face avant; sur la gauche, vers le haut, à droite et vers le bas) peut être répétée indéfiniment avec le même effet. L'effet de cette disposition est approximativement similaire a un ensemble d'aimant en fer à cheval adjacents, avec les pôles de même signes en contact.
Cet effet a été découvert par John C. Mallinson (en) en 1973, et ces structures à "flux d'un seul côté" ont été initialement considérées comme des « curiosités », bien qu'à l'époque le découvreur ait estimé que ceci pourrait améliorer de manière importante la technique des bandes magnétiques[3].
Le physicien Klaus Halbach, travaillant alors au Lawrence Berkeley National Laboratory durant les années 1980, inventa de son côté les réseaux de Halbach pour concentrer les faisceaux des accélérateurs de particules[4].
Réseaux de Halbach linéaires
Magnétisation

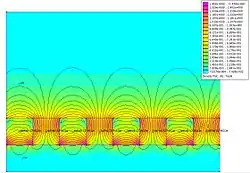
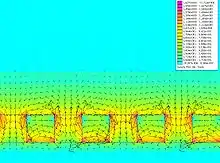
Bien que cette répartition de flux magnétique puisse paraître contre-intuitive à ceux qui sont familiers avec les aimants droits simples ou les solénoïdes, la cause de cette répartition de flux peut être visualisée intuitivement en utilisant les diagrammes originaux de Mallinson (notez que ceci utilise la composante négative y, contrairement a ce qu'on trouve dans l'article de Mallinson). Le diagramme montre le champ d'une bande de matériau ferromagnétique avec des magnétisations alternantes dans la direction y (en haut à gauche) et dans la direction x (en haut à droite). Notez que le champ au-dessus du plan est dans la même direction pour les deux structures, mais le champ sous le plan est dans une direction opposée. L'effet dû a une superposition de ces deux structures est montré dans la figure:
Le point critique est que le flux va être supprimé sous le plan et se renforcer au-dessus du plan. En fait, toute disposition des flux magnétiques décalés de les uns par rapports aux autres résulte en un flux unilatéral. La transformation mathématique qui décale la phase de tous les composants d'une fonction de est appelé transformation de Hilbert; les composants du vecteur de magnétisation peuvent alors être toute paire de transformation de Hilbert (La plus simple est simplement , comme montré dans le diagramme ci-dessus).
Le champ sur le côté fort d'un réseau idéal à variation continue est de la forme[5] :
ou:
- est le champ de forme
- est l'amplitude du champ à la surface du réseau
- est le numéro de en:wavenumber, (la répétition spatiale)
Applications
Les avantages d'une distribution unilatérale sont de deux ordres:
- Le champ est deux fois plus important du côté où le flux est confiné (dans un cas idéal).
- Il n'y a pas de champ magnétique parasite produit (dans un cas idéal) sur le côté opposé. Ceci aide au confinement des champs qui est une difficulté habituelle de la conception des structures magnétiques.
Bien qu'une distribution unilatérale de flux puisse sembler être un concept abstrait, les applications pratiques sont très variées, allant des aimants de réfrigérateur jusqu'aux applications industrielles telles les moteur sans balais, les bobinages de haut-parleur[6] la distribution ciblée de médicament[7], jusqu’à des applications de haute technologie comme le synchrotron wiggler, des aimants utilisés dans des accélérateurs de particules et des laser à électrons libres.
- Une suspension électrodynamique utilisant des aimants disposés en réseau de Halbach peut supporter un véhicule en mouvement sans asservissement électronique. Ce type de réseau est un composant essentiel de la voie de type en:Inductrack pour véhicule à sustentation magnétique de type maglev[8] et le système de lancement de fusée basé sur l'Inductrack[9] où le réseau de Halbach repousse des boucles de fil qui constituent la voie, après que le train ait été propulsé a une vitesse suffisante pour sa sustentation.
L'exemple le plus simple d'un aimant a flux unilatéral est un aimant de réfrigérateur. Ils sont généralement composé de poudre de ferrite dans un liant plastique ou élastomère. L'aimant extrudé est exposé à un champ tournant donnant aux particules magnétiques une magnétisation qui conduit à un flux unilatéral. Cette distribution accroit la force de maintien de l'aimant lorsqu'il est placé sur une surface perméable comparé à un aimant utilisant le même composé mais magnétisé de manière uniforme.
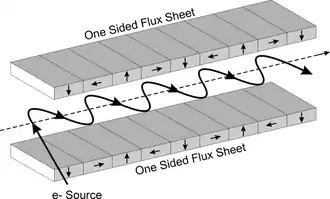
Étendre cette conception et ajouter une plaque supérieure donne un aimant wiggler, utilisé dans les synchrotrons et les laser à électrons libres. Les aimants Wiggler font osciller un faisceau d'électrons perpendiculairement au champ magnétique. Lors de leur accélération, les électrons irradient de l'énergie électromagnétiques dans leur axe, et comme ils interagissent avec la lumière émise, les photons le long de la ligne sont émis en phase, résultant en un faisceau lumineux monochromatique et cohérent similaire à celui d'un laser.
La disposition montrée ci-dessus est généralement dénommée "Halbach wiggler". Les vecteurs de magnétisation dans les plaques magnétisées tournent chacun dans une direction opposée; ci-dessus, le vecteur magnétique de la plaque supérieure tourne dans le sens des aiguilles d'une montre et le vecteur de magnétisation de la plaque inférieure tourne dans le sens trigonométrique. Cette conception est choisie pour que les composants x du champ magnétique des plaques s'annulent et que les composants y se renforcent et la valeur du champ est donnée par
ou k est le wavenumber de la plaque magnétique donné par l'espacement entre les blocs magnétiques ayant le même vecteur.
Réseaux linéaires variables


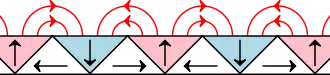
Une série de barres magnétiques, magnétisés perpendiculairement à leurs axes, peut être disposée en réseau de Halbach. Si chaque barre est ensuite tournée alternativement de 90°, le champ résultant passe d'une côté du plan à l'autre, comme montré de manière simplifiée dans le schéma.
Cette disposition permet en pratique au champ d'être allumé ou éteint dessus ou dessous le plan des barres suivant le rotation de celles-ci. Un tel dispositif est un système mécanique permettant de faire varier un champ sans avoir besoin de puissance électrique. Une étude détaillée de cette disposition a montré que chaque barre était soumise a un fort couple de la part des barres voisines et qu'un blocage mécanique était requis[13]. Une solution simple et efficace est d'installer des engrenages sur chaque barre de façon à obtenir une rotation alternative comme montré sur le schéma.
Cylindre de Halbach
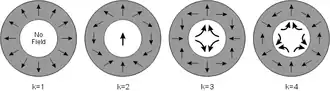
Un cylindre de Halbach est un cylindre magnétisé composé de matériaux ferromagnétiques produisant (dans un cas idéal) un champ magnétique intense entièrement confiné dans le cylindre avec un champ nul à l'extérieur. Le cylindre peut aussi être magnétisé de manière que le champ soit à l'extérieur avec un champ nul à l'intérieur. Plusieurs types de magnétisation sont proposés:
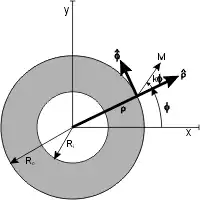
La direction de la magnétisation dans le matériau ferromagnétique, dans un plan perpendiculaire à l'axe du cylindre est donnée par
ou Mr est la rémanence ferromagnétique (A/m). Une valeur positive de k − 1 donne un champ magnétique interne et une valeur négative un champ magnétique externe.
Idéalement, ces structures pourraient être créées à partir d'un cylindre de longueur infinie avec la direction de la magnétisation variant continûment. Le champ magnétique produit par ce cylindre idéal serait parfaitement uniforme et totalement confiné à l'intérieur ou à l'extérieur du cylindre. Ce n'est pas réalisable en pratique et la longueur réelle limitée des cylindres produits des "effets d'extrémité" qui introduisent des discontinuités dans le champ[14],[15]. La difficulté de fabrication d'un cylindre avec un champ variant continûment conduit généralement à une conception en segments.
Applications
Ces structures cylindriques sont utilisées dans des équipements tels que les moteurs sans balais, les coupleurs magnétiques et les cylindres à haut flux. Les moteurs sans balais et les coupleurs magnétiques utilisent des dispositions multipôles :
- Les moteurs sans balais utilisent typiquement des dispositions cylindriques dans lesquelles le flux est confiné au centre du trou (telle que k = 4 au-dessus, un rotor à six pôles) avec les bobinages installés dans le trou. Une telle conception de moteur qui fait écran à son propre champ magnétique a un meilleur rendement et produit un couple supérieur à une disposition conventionnelle.
- Les coupleurs magnétiques transmettent un couple au travers d'une barrière transparente aux champs magnétiques (soit la barrière est amagnétique soit elle n'est pas affectée par le champ magnétique appliqué), par exemple au travers de containers scellés ou d'appareils à pression. Le coupleur optimal est construit avec une paire de cylindres coaxiaux emboités avec des flux magnétiques contraires +k and −k, car cette configuration est le seul système ou une cylindre de longueur infinie peut transmettre un couple[16]. À l'état énergétique minimal, le flux externe du cylindre intérieur est exactement le même que le flux interne du cylindre extérieur. Tourner un cylindre relativement à l'autre rétablit le couple.
- Des paliers électrodynamiques avec un ou plusieurs réseaux de Halbach fermés concentriques à l'arbre assurent le centrage d'une masse tournante sans asservissement électronique.
Champs uniformes
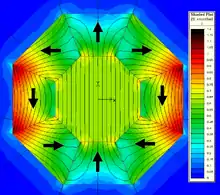
Pour le cas particulier ou k = 2, le champ est uniforme et donné par
ou les rayons des cylindre intérieur et extérieur sont respectivement Ri and Ro . H est dans la direction y. Ceci est la disposition la plus simple du cylindre de Halbach, et on peut voir que si le ratio entre le rayon extérieur et le rayon intérieur est plus grand que e, le flux dans la cavité dépasse la rémanence du matériau magnétique utilisé pour fabriquer le cylindre. Cependant, des précautions sont nécessaires pour éviter de créer un champ qui dépasse la coercibilité des aimants permanent utilisés car cela pourrait conduire à la démagnétisation du cylindre et à produire un champ magnétique beaucoup plus faible que prévu[17],[18].

Cette disposition cylindrique est seulement un type de conception qui produit un champ uniforme dans une cavité interne à un réseau de Halbach fait avec des aimants permanents. Il existe d'autres types de conceptions incluant des formes en coin, proposées par Abele and Jensen, dans lesquels des 'coins' en matériau magnétique sont disposés pour fournir un champ uniforme à l'intérieur des cavités comme montré.
La direction de la magnétisation des 'coins' en (A) peut être calculée en utilisant un jeu de règles donné par Abele et permet une grande liberté dans la forme de la cavité. Un autre type de disposition est le 'mangle' magnétique (B), proposé par Coey et Cugat[19],[20], dans lequel des barres uniformément magnétisées sont disposées de manière à créer un cylindre de Halbach, comme montré dans la conception à 6 barres. Cette disposition améliore largement l'accès à la zone où le champ est uniforme, au prix d'un champ de taille plus modeste que dans une disposition cylindrique (bien que cette zone puisse être agrandie en augmentant le nombre de barres). Tourner les barres l'une par rapport à l'autre offre de nombreuses possibilités d'ajustement y compris la possibilité d'avoir un champ variable et des configurations dipolaires. On peut voir que les conceptions montrées en (A) et (B) sont étroitement liées au cylindre de Halbach k = 2. D'autre dispositions très simples pour un champ uniforme comprennent des aimants séparés par des éléments de recirculation en fer doux, comme montré dans la figure (C).
Dans les dernières années, ces dipôles de Halbach ont été utilisés pour conduire des expériences de bas champ NMR[21]. Comparé aux géométries à aimants permanents (Bruker Minispec) disponibles dans le commerce, elles offrent, comme expliqué ci-avant une grande cavité tout en maintenant un champ relativement homogène.
Champs variables
Les cylindres de Halbach donnent un champ statique. Mais les cylindres peuvent être encastrés, et en tournant l'un par rapport à l'autre, il est possible d'ajuster et d'annuler le champ[22]. Comme le champ à l'extérieur d'un cylindre est faible, Il n'y a pratiquement pas d'effort nécessaire pour orienter un cylindre par rapport à l'autre.

Sphères de Halbach
Si la disposition bidimensionnelle des cylindres de Halbach est étendue à trois dimensions, le résultat est une sphère de Halbach. Cette disposition a un champ très uniforme à l'intérieur car elle n'est pas perturbée par les "effets de bord" d'un cylindre de longueur finie. L'amplitude du champ uniforme pour une sphère augmente vers les 4/3 d'un cylindre idéal ayant les mêmes diamètres intérieurs et extérieurs. Cependant, du fait de la forme sphérique, l'accès a la région de champ uniforme est généralement limité à un trou d'accès étroit sur le haut et le bas du dispositif.
L'équation du champ dans une sphère de Halbach est[23]
Des champs plus importants sont possibles en optimisant le dessin sphérique pour prendre en compte le fait que la sphère est composée de dipôles ponctuels (et non en ligne). Ceci résulte en une déformation de la sphère vers un ellipsoïde qui donne une distribution magnétique non-uniforme sur les composants de la sphère. En utilisant cette méthode, et aussi des pôles non magnétisés, on a pu obtenir un champ de 4,5 T dans un volume de 20 mm3: Bloch et al. in 1998[24], et ceci a encore été augmenté a 5 T in 2002[25], cependant avec un volume moindre de 0,05 mm3. Comme les champs des aimants permanent dépendent de leur température, la réfrigération de l'ensemble du réseau peut augmenter le champ de la zone comme démontré par Kumada et al. Ce groupe a aussi signalé le développement d'un dipôle cylindrique de Halbach de 5,16 T en 2003[26].
Bobinages de Halbach
Un réseau de Halbach peut être fait avec des bobinages. Le bobinage d'un réseau de Halbach a naturellement une inductance plus faible qu'un bobinage ordinaire. Ce qui fait qu'un bobinage en réseau de Halbach peut produire un champ magnétique relativement élevé pour une plus faible inductance et avoir un meilleur facteur de puissance comparé aux bobinages courants[27].
Voir aussi
- Aimant au néodyme
- Aimant permanent
- Aimant de terre rare
- Focalisation forte
- La voie de type en:Inductrack utilise des réseaux de Halbach pour générer des champs importants pour un système de transport de type maglev
- Loi de Lenz-Faraday
- Les Bobines de Helmholtz peuvent fournir des champs magnétiques très réguliers
Références
- Klaus Halbach, « Design of permanent multipole magnets with oriented rare earth cobalt material », Nuclear Instruments and Methods, vol. 169, no 1, , p. 1–10 (ISSN 0029-554X, DOI 10.1016/0029-554X(80)90094-4, Bibcode 1980NucIM.169....1H, lire en ligne)
- Klaus Halbach, « Applications of Permanent Magnets in Accelerators and Electron Storage Rings », Journal of Applied Physics, vol. 57, no 1, , p. 3605–3608 (ISSN 0029-554X, DOI 10.1063/1.335021, Bibcode 1985JAP....57.3605H, lire en ligne)
- J.C. Mallinson, "One-Sided Fluxes — A Magnetic Curiosity?", IEEE Transactions on Magnetics, 9, 678–682, 1973, DOI:10.1109/TMAG.1973.1067714
- « Magnetically levitated train takes flight | US Department of Energy Science News | EurekAlert! Science News », sur eurekalert.org
- « Archived copy » [archive du ] (consulté le )
- « High efficiency voice coil motor »
- A. Sarwar, A. Nemirovski et B. Shapiro, « Optimal Halbach permanent magnet designs for maximally pulling and pushing nanoparticles », Journal of Magnetism and Magnetic Materials, vol. 324, no 5, , p. 742–754 (PMID 23335834, PMCID 3547684, DOI 10.1016/j.jmmm.2011.09.008, Bibcode 2012JMMM..324..742S, lire en ligne)
- Richard F. Post, « Toward More Efficient Transport: The Inductrack Maglev System », Lawrence Livermore National Laboratory, (consulté le )
- L. S. Tung, R. F. Post et J. Martinez-Frias, « Final progress report for the NASA Inductrack model rocket launcher at the Lawrence Livermore National Laboratory », Laboratoire national Lawrence Livermore, (lire en ligne [archive du ], consulté le )
- Analysis and Case Study of Permanent Magnet Arrays for Eddy Current Brake Systems with a New Performance Index
- Design of Double-Sided Linear Permanent Magnet Eddy CurrentBraking System
- The application of linear Halbach array to eddy current rail brake system
- J. E. Hilton et S. M. McMurry, « An adjustable linear Halbach array », Journal of Magnetism and Magnetic Materials, vol. 324, no 13, , p. 2051–2056 (DOI 10.1016/j.jmmm.2012.02.014, Bibcode 2012JMMM..324.2051H, hdl 2262/63909, lire en ligne)
- T. R. Ni Mhiochain, D. Weaire, S. M. McMurry et J. M. D. Coey, « Analysis of torque in nested magnetic cylinders », Journal of Applied Physics, vol. 86, no 11, , p. 6412–6424 (DOI 10.1063/1.371705, Bibcode 1999JAP....86.6412N)
- R. Bjørk, « The ideal dimensions of a Halbach cylinder of finite length », Journal of Applied Physics, vol. 109, no 1, , p. 013915–013915–6 (DOI 10.1063/1.3525646, Bibcode 2011JAP...109a3915B, arXiv 1410.0496)
- R. Bjørk, A. Smith et C. R. H. Bahl, « Analysis of the magnetic field, force, and torque for two-dimensional Halbach cylinders », Journal of Magnetism and Magnetic Materials, vol. 322, no 1, , p. 133–141 (DOI 10.1016/j.jmmm.2009.08.044, Bibcode 2010JMMM..322..133B, arXiv 1409.1712, lire en ligne)
- R. Bjørk, A. Smith et C. R. H. Bahl, « The efficiency and the demagnetization field of a general Halbach cylinder », Journal of Magnetism and Magnetic Materials, vol. 384, , p. 128–132 (DOI 10.1016/j.jmmm.2015.02.034, Bibcode 2015JMMM..384..128B, arXiv 1502.06700, lire en ligne)
- A. R. Insinga, C. R. H. Bahl, R. Bjørk et A. Smith, « Performance of Halbach magnet arrays with finite coercivity », Journal of Magnetism and Magnetic Materials, vol. 407, , p. 369–376 (DOI 10.1016/j.jmmm.2016.01.076, Bibcode 2016JMMM..407..369I)
- J. M. D. Coey et T.R. Ní Mhíocháin, High Magnetic Fields : Science and Technology, vol. Volume 1, World Scientific Publishing, , 25–47 p. (ISBN 978-981-02-4964-9), « Permanent Magnets »
- O. Cugat, F. Bloch et J.C. Toussaint, « 4-Tesla Permanent Magnetic Flux Source », Proc. 15th International Workshop on Rare Earth Magnets and Their Applications, , p. 807
- (en) H. Raich et P. Blümler, « Design and construction of a dipolar Halbach array with a homogeneous field from identical bar magnets: NMR Mandhalas », Concepts in Magnetic Resonance Part B-Magnetic Resonance Engineering, vol. 01/2004, no 23B, , p.16–25.
- « Tip Magazine: Magnets, Markets, and Magic Cylinders The Industrial Physicist by Michael Coey and Denis Weaire » [archive du ]
- Permanent magnet based sources of magnetic field.
- Bloch, F. and Cugat, O. and Meunier, G. and Toussaint, J.C., « Innovating approaches to the generation of intense magnetic fields: design and optimization of a 4 Tesla permanent magnet flux source », IEEE Transactions on Magnetics, vol. 34, no 5, , p. 2465–2468 (DOI 10.1109/20.717567, Bibcode 1998ITM....34.2465B)
- « Record-breaking magnet has five-tesla field – CERN Courier »
- Kumada, M. and Antokhin, E.I. and Iwashita, Y. and Aoki, M. and Sugiyama, E., « Super Strong Permanent Magnet Quadrupole for a Linear Collider », IEEE Transactions on Applied Superconductivity, vol. 14, no 2, , p. 1287–1289 (DOI 10.1109/TASC.2004.830555, Bibcode 2004ITAS...14.1287K, lire en ligne)
- « STUDY OF HALBACH ARRAY WINDING »
Liens externes
- Passive levitation of a shaft
- Electric model aircraft motor
- magnet levitated vehicle switching system
- Portail de la physique