Relaxation de Debye

On imagine une situation dans laquelle on applique champ électrique à un milieu diélectrique, on attend suffisamment longtemps pour atteindre un état stable présentant une polarisation induite ${\displaystyle P_{0}}$ qui dépend de la susceptibilité diélectrique du milieu, puis on coupe le champ électrique. La polarisation en fonction du temps d'un système suivant une relaxation de Debye suit par définition une simple loi exponentielle avec une constant de temps ${\displaystyle \tau }$:

${\displaystyle P(t)=P_{0}\exp(-t/\tau ).}$

Schéma de la réponse diélectrique complexe correspondant à une relaxation de Debye.

La réponse diélectrique complexe d'un milieu en présence d'une relaxation de Debye s'écrit, dans le domaine des fréquences,

${\displaystyle \varepsilon (\omega )=\varepsilon _{\infty }+{\frac {\Delta \varepsilon }{1+j\omega \tau }}}$

où ${\displaystyle \varepsilon _{\infty }}$ désigne la constante diélectrique dans la limite des très hautes fréquences et ${\displaystyle \Delta \varepsilon }$ est la contribution de ce processus de relaxation à la constante diélectrique mesurée à basses fréquences. Les parties réelle et imaginaire s'écrivent

${\displaystyle {\begin{aligned}\varepsilon '(\omega )&=\varepsilon _{\infty }+{\frac {\Delta \varepsilon }{1+\omega ^{2}\tau ^{2}}}\\\varepsilon ''(\omega )&={\frac {\omega \tau \,\Delta \varepsilon }{1+\omega ^{2}\tau ^{2}}}.\end{aligned}}}$

Il existe plusieurs manières usuelles de représenter cette réponse. Les parties réelles et imaginaires sont représentées en fonction de la fréquences (en échelle logarithmique) sur la figure ci-contre. Une autre représentation courante dans le context de la spectroscopy diélectrique est le diagramme Cole-Cole dans lequel on trace la partie imaginaire en fonction de la partie réelle. Dans ce diagramme, la signature d'une relaxation de Debye est un simple demi-cercle.

Circuit RC

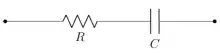
En spectroscopie diélectrique, il est courant de modéliser la réponse d'une système par un circuit équivalent, c'est-à-dire présentant la même réponse en fréquence. Pour une relaxation de Debye, le circuit équivalent est un simple circuit RC composé d'une résistance et d'un condensateur en série[6].

L'impédance complexe de ce circuit RC est donnée par

${\displaystyle Z^{*}(\omega )=R+{\frac {1}{jC\omega }}}$

L'équivalence avec la relaxation de Debye apparaît clairement quand on exprime cette impédance sous la force d'une capacité effective complexe:

${\displaystyle C_{\mathrm {eff} }^{*}(\omega )={\frac {1}{Z^{*}(\omega )\,j\omega }}={\frac {C}{1+j\tau \omega }}}$

Un simple système à deux états suffit à conduire au modèle de Debye[7]. On considère un système de particules identiques, indépendantes, chacune plongée dans un double puits de potentiel et possédant deux états d'équilibre (deux minimas) associés à un moment dipolaire ${\displaystyle -p}$ et ${\displaystyle +p}$. On peut noter ${\displaystyle n_{+}}$ et ${\displaystyle n_{-}}$ les nombres de molécules dans les états ${\displaystyle -}$ et ${\displaystyle +}$ respectivement. La polarization totale ${\displaystyle P}$ s'écrit alors ${\displaystyle p(n_{+}-n_{-})}$. Le système est à la température ${\displaystyle T}$. Du fait de l'agitation thermique, chaque molécule a une certaine probabilité de changer d'état. On peut ainsi définir un taux de transition ${\displaystyle \Gamma _{+-}}$ comme étant le nombre de particules passant de l'état ${\displaystyle +}$ à l'état ${\displaystyle -}$ par unité de temps.

En l'absence de champ électrique, les deux états sont équivalents de sorte que ${\displaystyle n_{+}=n_{-}}$ et ${\displaystyle P=0}$, et ${\displaystyle \Gamma _{+-}=\Gamma _{-+}=\Gamma }$. Lorsqu'un champ électrique ${\displaystyle E}$ est appliqué, l'équivalence entre les deux états est brisée; une particule dans l'état ${\displaystyle \pm }$ a une énergie ${\displaystyle \pm pE}$. Les populations des états à l'équilibre suivent la statistique de Boltzmann :

${\displaystyle {\frac {n_{+}}{n_{-}}}=\exp(2pE/k_{B}T)}$

Partant de cet état d'équilibre, on coupe le champ électrique à ${\displaystyle t=0}$. L'évolution dans le temps du nombre de particules dans les états ${\displaystyle +}$ et ${\displaystyle -}$est alors régie par

${\displaystyle {\frac {\mathrm {d} n_{+}}{\mathrm {d} t}}=-{\frac {\mathrm {d} n_{-}}{\mathrm {d} t}}=-n_{+}\Gamma +n_{-}\Gamma }$

En écrivant l'équation régissant l'évolution de la polarisation total ${\displaystyle P}$, il vient

${\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} t}}={\frac {\mathrm {d} }{\mathrm {d} t}}[p(n_{+}-n_{-})]=2p\Gamma (-n_{+}+n_{-})=-2\Gamma P(t)}$

On y reconnaît une équation différentielle du premier ordre qui s'intégre pour donner le modèle de Debye, où le temps de relaxation introduit précédemment apparaît comme ${\displaystyle \tau =1/(2\Gamma )}$.

Les exemples de matériaux solides présentant un comportement idéal de Debye sont assez rares[8]. Un exemple quasi idéal peut être trouvé dans le cristal ferroélectrique CsH₂PO₄ [9]^,[10]. Ce cristal appartient à la famille des ferroélectriques à liaison hydrogène dans lesquels des protons sont situés le long d'une liaison chimiques entre deux oxygènes. A basses températures, dans la phase ferroélectrique, le proton occupe une de ces deux positions. En revanche, au-dessus de la température de transition ferroélectrique, il a suffisamment d'énergie pour sauter entre les deux positions d'équilibres, ce qui fournit une bonne réalisation pratique d'un système à deux états.