Ressort (mécanique élémentaire)

Système masse-ressort de traction (gauche), isolement du ressort (milieu) et isolement de la masse (droite).

Système masse-ressort de compression (gauche), isolement du ressort (milieu) et isolement de la masse (droite).

Loi des ressorts, pour les ressorts de traction (vert) et les ressorts de compression (violet). La force résultante F_res est celle subie (ressentie) par le doigt qui déforme le ressort. En pratique, la loi pour les ressorts de traction est décalée (pointillés).

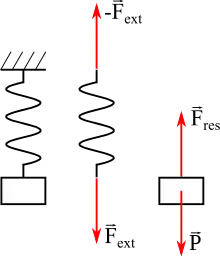
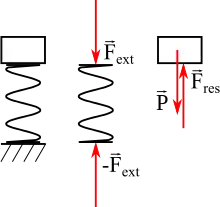
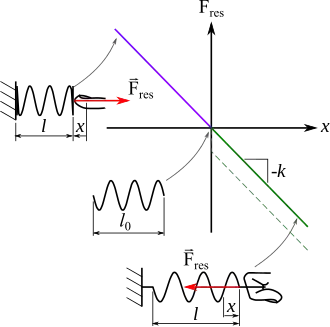
Le ressort a une longueur à vide l₀. Si on veut l'allonger (ressort de traction) ou le raccourcir (ressort de compression) d'une longueur x nommée allongement ou élongation, il faut exercer deux forces égales et opposées à ses extrémités ; la force ${\displaystyle {\vec {F}}_{\mathrm {ext} }}$ à une des extrémités est orientée dans l'axe du ressort et son intensité vaut ${\displaystyle \|{\vec {F}}_{\mathrm {ext} }\|=F_{ext}=k\,|x|}$, où k est la constante de proportionnalité, appelée « constante de raideur » ou constante de rappel du ressort, exprimée en newtons par mètre (N/m ou N m⁻¹).

D'après le principe des actions réciproques (3^e loi de Newton), la force ${\displaystyle {\vec {F}}_{\mathrm {res} }}$ qu'exerce le ressort vaut :

${\displaystyle {\vec {F}}_{\mathrm {res} }=-{\vec {F}}_{\mathrm {ext} }}$.

L'élongation x est une longueur algébrique ; par convention, on la prend positive dans le cas de l'allongement et négative dans le cas de la compression : la longueur finale du ressort vaut ${\displaystyle l=l_{0}+x}$.

Par convention, l'intensité ${\displaystyle F_{\mathrm {res} }}$ de la force qu'exerce le ressort ${\displaystyle {\vec {F}}_{\mathrm {res} }}$ est également une valeur algébrique, prise positive dans le cas de la compression et négative dans le cas de la traction. On a donc de manière générale :

${\displaystyle F_{\mathrm {res} }=-k\,x}$.

Dans cette étude élémentaire, on ne distingue pas le ressort de traction du ressort de compression, alors que technologiquement les deux sont bien distincts. On travaille donc avec les hypothèses suivantes :

• les spires sont non jointives ;
• il n'y a pas de dissipation d'énergie (la force est conservative) ;
• on reste dans un domaine où la réponse est toujours linéaire (la déformation est limitée).

Le travail de la force extérieure pour passer d'un allongement nul à un allongement X est

${\displaystyle W_{{\vec {F}}_{\mathrm {ext} }}=\int _{0}^{X}-F_{\mathrm {ext} }\,\mathrm {d} x=-\int _{0}^{X}k\,x\,\mathrm {d} x}$,

d'où :

${\displaystyle W_{{\vec {F}}_{\mathrm {ext} }}=-{\frac {1}{2}}\,k\,X^{2}}$.

On peut ainsi définir l'énergie potentielle élastique E_pe d'un ressort d'allongement X :

${\displaystyle E_{pe}={\frac {1}{2}}\,k\,X^{2}}$.

Ressort et étude de balistique

Ressort de compression (dessin).

Ressort de compression (photographie).

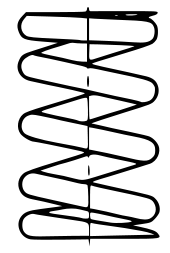
On prend souvent le cas d'une bille propulsée par un ressort ; il s'agit dans ce cas-là d'un ressort de compression (à spires non jointives). Si l'on néglige les frottements, ce système permet d'écrire la conservation de l'énergie mécanique, ce qui permet de déterminer la vitesse de la bille lorsqu'elle quitte le ressort, puis de mener l'étude de chute libre classique.

Pendule pesant

Oscillations harmoniques d'un pendule pesant.

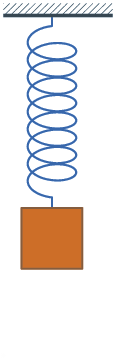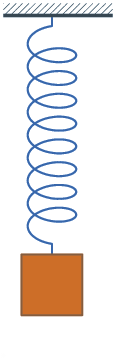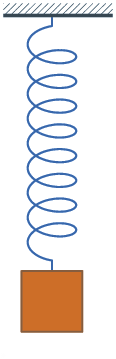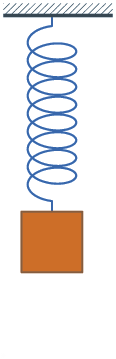
Le pendule pesant est un ressort de traction au bout duquel on accroche une masse ; lorsque le système est au repos (la masse est immobile dans le référentiel du laboratoire), le ressort a un allongement non nul, les spires sont non jointives. Par rapport à cette position de repos, on peut donc étirer ou comprimer le système (mais le ressort restera en traction).

Si l'on tire la masse vers le bas et qu'ensuite on la lâche, le système va osciller. Ceci permet d'aborder les oscillations harmoniques et les équations différentielles permettant cette étude.

On peut mettre une sollicitation périodique en haut du ressort, par exemple un système de manivelle tournant imposant une force dont l'intensité varie dans le temps selon une loi sinusoïdale. On peut ainsi étudier les oscillations forcées.

On peut plonger la masse dans un récipient d'eau afin d'augmenter les frottements et ainsi étudier les oscillations amorties ou les oscillations forcées avec dissipation.

On étudie fréquemment la torsion d'un fil ; on prend le fil vertical afin de ne pas avoir à prendre le poids en compte. Tant que la sollicitation reste faible, le couple Γ à appliquer est proportionnel à l'angle de torsion θ :

${\displaystyle \Gamma =-C\,\theta }$

où C est la raideur du ressort.

On peut se servir de ce système pour étudier les forces électrostatiques (balance de torsion), ou encore les oscillations (pendule de torsion). C'est aussi une balance de torsion qui a permis de déterminer la constante universelle de gravitation (expérience de Cavendish).

C'est aussi le modèle pour un certain nombre de dispositifs comme l'ampèremètre dit « balistique ».

Un mécanisme est un assemblage de pièces dont un certain nombre sont en mouvement. Ce mouvement est créé grâce à un effort (principe fondamental de la dynamique), et cet effort est variable (puisque le mouvement a un début et une fin). Les pièces vont donc subir des actions mécaniques d'intensité variable, et ainsi leur déformation élastique va varier.

Pour étudier l'influence de ces déformations élastiques, et en particulier le déphasage (retard entre la loi d'entrée et la loi de sortie) et les vibrations, on remplace fréquemment chaque pièce par un système masse-ressort. On choisit donc un ressort équivalent :

• on sélectionne le mode de déformation principal de la pièce ;
• on en déduit un type de ressort (traction/compression, flexion, torsion) ;
• on détermine sa raideur, par essai mécanique ou par calcul par éléments finis.

• Système masse-ressort
• Ressort

• Portail du génie mécanique
• Portail de la physique