Small-Scale Experimental Machine

La Small-Scale Experimental Machine (SSEM) (« machine expérimentale à petite échelle »), surnommée Baby (« Bébé »), était la première machine à architecture de von Neumann du monde. Construite à l’université Victoria de Manchester par Frederic Calland Williams, Tom Kilburn et Geoff Tootill, elle exécuta son premier programme le [1].

Réplique de la Small-Scale Experimental Machine (SSEM) au musée des sciences et de l'industrie de Manchester.

Cette machine ne fut pas construite pour son utilité pratique en tant qu'ordinateur, mais comme un banc de test pour le tube de Williams, une forme primitive de mémoire d'ordinateur. Bien que considérée comme « petite et primitive » selon les standards de son époque, elle fut la première machine fonctionnelle contenant tous les éléments essentiels d'un ordinateur électronique moderne[2]. Dès que la SSEM eut démontré la faisabilité de sa conception, un projet fut lancé à l'université de Manchester pour la développer afin d'en faire un ordinateur plus utilisable, le Manchester Mark I. Le Mark I, à son tour, devint rapidement le prototype du Ferranti Mark I, le premier ordinateur généraliste commercialisé[3].

La SSEM utilisait des mots de 32 bits et une mémoire de 32 mots. Comme elle était conçue pour être l'ordinateur à programme enregistré en mémoire le plus simple possible, les seules opérations arithmétiques implantées dans le matériel étaient la soustraction (moins binaire) et l'opposé (moins unaire) ; les autres opérations arithmétiques étaient réalisées par des programmes. Le premier des trois programmes écrits pour la machine trouva le plus grand diviseur propre de 218 (262 144), un calcul dont on savait qu'il prendrait un temps important pour s'exécuter, en testant chaque entier de 218−1 à 1 dans l'ordre décroissant, car il fallait réaliser les divisions par des soustractions itérées du diviseur. Le programme consistait en 17 instructions et fonctionna pendant 52 minutes avant d'atteindre la réponse correcte, 131 072. La SSEM effectua 3,5 millions d'opérations pour ce calcul, ce qui donne une vitesse de 1,1 kIPS.

Contexte

De la machine de Turing à l'architecture de von Neumann
Vue d'artiste d'une machine de Turing

Le premier calculateur contrôlé par un programme fut la machine analytique construite par Charles Babbage en 1834. Un siècle plus tard, en 1936, le mathématicien Alan Turing publia sa description de ce qui est désormais connu sous le nom de machine de Turing, un concept théorique destiné à explorer les limites du calcul mécanique. Turing n'imaginait pas une machine physique mais une personne, qu'il appelait un « calculateur »[4], qui suivait les instructions fournies par une bande sur laquelle on pouvait lire et écrire des symboles séquentiellement au fur et à mesure qu'elle passait sous une tête de lecture/écriture. Turing prouva que s'il est possible d'écrire un algorithme pour résoudre un problème mathématique, alors une machine de Turing peut exécuter cet algorithme[4] .

Le Z3 de Konrad Zuse fut la première machine programmable fonctionnelle du monde. Entièrement automatique, à base de circuits binaires numériques, il n'avait cependant pas les branchements conditionnels d'une machine de Turing. En , il fut présenté avec succès devant un public de scientifiques du Deutsche Versuchsanstalt für Luftfahrt (« Laboratoire allemand pour l'aviation ») à Berlin[5]. Le programme du Z3 était enregistré sur une bande externe, mais elle était électromécanique plutôt qu'électronique. Le Colossus, fabriqué en 1943, fut le premier instrument de calcul électronique, mais ne faisait que du décryptage et n'était donc pas une machine généraliste.

L'ENIAC fut, en 1946, la première machine électronique généraliste. Il était Turing-complet, avec des branchements conditionnels, et programmable pour résoudre une large gamme de problèmes. Cependant, son programme était enregistré dans l'état d'interrupteurs dans des câbles, et non en mémoire, en sorte qu'il pouvait falloir plusieurs jours pour le reprogrammer[2]. Des chercheurs tels que Turing et Konrad Zuse explorèrent l'idée d'utiliser la mémoire de l'ordinateur pour contenir le programme et les données sur lesquelles il travaillait[6], mais on considère généralement que c'est le mathématicien John von Neumann qui a défini cette architecture d'ordinateur, toujours utilisée dans presque tous les ordinateurs[7].

Du radar à l'ordinateur
Principe de l'architecture de von Neumann

La construction d'un ordinateur de von Neumann dépendait de la disponibilité d'un support de mémoire sur lequel enregistrer le programme. Pendant la Seconde Guerre mondiale, des chercheurs travaillant sur le problème d'éliminer les échos parasites des signaux radar avaient développé une forme de mémoire à ligne de délai, dont la première application fut la ligne de délai au mercure[8] développée par John Presper Eckert. Les transmetteurs radar envoient des pulsations d'énergie radio brèves et régulières, dont les reflets sont affichés sur un écran à tube cathodique. Comme les opérateurs ne s'intéressent habituellement qu'aux cibles mouvantes, il était désirable d'éliminer les reflets d'objets stationnaires. Ce filtrage était réalisé en comparant chaque pulsation reçue avec la précédente et en rejetant les deux si elles étaient identiques, ce qui résultait en un signal qui ne contenait que les images d'objets en mouvement. Afin d'enregistrer chaque pulsation reçue pour une comparaison ultérieure, elle passait par une ligne de transmission, ce qui la retardait exactement du temps séparant deux pulsations transmises[9].

Turing arriva au laboratoire national de physique (NPL) de Teddington (Richmond upon Thames, grand Londres) en octobre 1945[10]. À ce moment, des scientifiques du ministère de l'équipement des armées avaient conclu que la Grande-Bretagne avait besoin d'un laboratoire national de mathématiques pour coordonner le calcul assisté par machine[11]. Une division de mathématiques fut mise en place au NPL, et le , Alan Turing présenta un article décrivant sa conception d'un calculateur électronique à programme enregistré en mémoire connu sous le nom d'Automatic Computing Engine (ACE) (« moteur de calcul automatique »)[11]. Ce fut l'un des multiples projets lancés dans les années suivant la Seconde Guerre mondiale dans le but de construire un calculateur à programme enregistré en mémoire. Approximativement au même moment, l'EDVAC était en développement à l'école Moore d'ingénieurs électriciens de l'université de Pennsylvanie, et le laboratoire de mathématiques de l'université de Cambridge travaillait sur l'EDSAC[11],[12].

Les responsables du projet au NPL n'avaient pas l'expertise nécessaire à construire une machine comme l'ACE, ils contactèrent donc Tommy Flowers au centre de recherches du bureau de Poste général. Flowers, qui avait conçu Colossus, le premier ordinateur électronique programmable au monde, avait d'autres engagements et ne put prendre part au projet. Cependant, son équipe construisit quelques lignes de délai pour l'ACE[11]. Ils demandèrent aussi de l'aide au Telecommunications Research Establishment (TRE) (« établissement de recherches en télécommunications ») et à Maurice Wilkes, du laboratoire de mathématiques de l'université de Cambridge[11].

Les responsables du NPL au gouvernement décidèrent que, comme tout le travail était effectué par le TRE en son nom, l'ACE devait recevoir la priorité maximale[11]. La décision du NPL conduisit à une visite du surintendant de la division de physique du TRE le , en compagnie de Frederic Calland Williams et A. M. Uttley, lui aussi du TRE[11]. Williams dirigeait un groupe de développement du TRE qui travaillait sur les supports de mémoire CRT pour les appliquer aux radars, en lieu et place des lignes de délai[13]. Il avait déjà accepté un poste de professeur à l'université Victoria de Manchester, et la plupart de ses techniciens de circuits étaient en cours de transfert vers le département de l'énergie atomique[11]. Le TRE accepta d'aider un petit groupe de techniciens placé sous la direction de Williams à l'université et de soutenir un autre petit groupe travaillant avec Uttley au TRE[11].

Le tube de Williams

Les premiers ordinateurs, comme le CSIRAC, exploitaient des lignes de délai au mercure[14]. Cependant, cette technologie avait des inconvénients : elle était lourde, coûteuse, et ne permettait pas l'accès aléatoire. De plus, comme les données étaient enregistrées comme une séquence d'ondes acoustiques propagées dans une colonne de mercure, il fallait contrôler très attentivement la température de la machine, car la vitesse du son dans un milieu varie avec sa température. Williams avait vu une expérience à Bell Labs qui montrait l'efficacité de tubes cathodiques (CRT) comme alternative aux lignes de délai pour enlever l'écho de terre des signaux radar. Alors qu'il travaillait au TRE, peu avant d'arriver à l'université de Manchester en , il avait développé une forme de mémoire électronique connue sous le nom de tube de Williams, basée sur un CRT standard, qui était le premier support d'enregistrement numérique à accès aléatoire[15]. La Small-Scale Experimental Machine fut conçue pour prouver la viabilité du tube de Williams comme support d'enregistrement, en vérifiant que les données qu'il contenait pouvaient être mises à jour continuellement avec la vitesse nécessaire pour permettre leur utilisation par un ordinateur[16],[17].

Pour être utilisable dans un ordinateur numérique binaire, le tube devait pouvoir enregistrer l'un ou l'autre de deux états dans chacun de ses emplacements de mémoire, pour représenter les bits 0 et 1. Il exploitait la charge électrostatique générée en affichant soit un trait, soit un point à chaque position sur l'écran CRT. Ce phénomène est appelé émission secondaire. Un trait générait une charge positive et un point une charge négative. Une plaque de détection en face de l'écran recevait la charge, qui représentait 0 si elle était négative, 1 si elle était positive. La charge se dissipait en environ 0,2 seconde, mais elle pouvait être automatiquement rafraîchie à partir des données captées par le détecteur[18]. Au départ, le tube de Williams était basé sur le CV1131, un CRT du commerce de 30 cm de diamètre, mais un tube plus petit, de 15 cm de diamètre, le CV1097, fut utilisé dans la SSEM[19].

Développement et conception
Schéma de l'architecture montrant comment les quatre tubes cathodiques (en vert) étaient déployés

Nommé à la chaire d'ingénierie électrique de l'université de Manchester, Williams recruta son collègue du TRE Tom Kilburn comme assistant. À l'automne 1947, les deux scientifiques avaient augmenté la capacité de stockage du tube de Williams d'un bit à 2 048, disposés en une matrice de 64 bits par 32[20], et montré qu'il était possible de conserver ces bits pendant quatre heures[16]. L'ingénieur Geoff Tootill se joignit à l'équipe, détaché du TRE en , et resta comme assistant jusqu'en [21].

Max Newman avait été nommé à la chaire de mathématiques pures de l'université de Manchester en 1945. Pendant la Seconde Guerre mondiale, il avait travaillé comme cryptanalyste à Bletchley Park et dirigé l'équipe qui, en 1943, avait produit le premier des ordinateurs casseurs de code Colossus. Bien que Newman n'ait joué aucun rôle actif dans le développement de la SSEM, pas plus qu'aucun des ordinateurs Manchester qui suivirent, il soutenait ce projet qui l'enthousiasmait, et organisa l'acquisition de fournitures issues de surplus de guerre pour sa construction, y compris des casiers métalliques du bureau de Poste général de Bletchley[22].

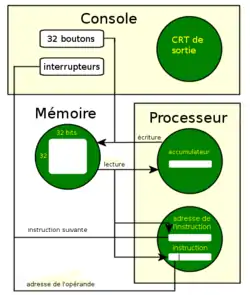
En , la SSEM était construite et fonctionnait[20]. Elle était longue de 5,2 m, haute de 2,2 m, et pesait presque une tonne. La machine contenait 550 tubes électroniques, 300 diodes et 250 pentodes, et consommait 3 500 watts[23]. L'unité arithmétique était faite de tubes électroniques EF50 (des pentodes Philips), largement utilisés pendant la guerre[16]. La SSEM utilisait un tube de Williams pour fournir 32 mots de 32 bits de mémoire vive, un deuxième hébergeait l'accumulateur dans lequel les résultats intermédiaires d'un calcul étaient temporairement enregistrés, et un troisième contenait l'instruction en cours d'exécution et son adresse en mémoire. Un quatrième CRT, non équipé de l'électronique destinée au stockage des trois autres, était utilisé comme périphérique de sortie. Il pouvait afficher les bits contenus dans tout autre tube[24].

Le CRT de sortie est juste au-dessus du périphérique d'entrée, flanqué du moniteur et de l'électronique de contrôle

Chaque mot de 32 bits de la RAM pouvait contenir soit une instruction de programme, soit des données. Dans une instruction de programme, les bits 0 à 12 représentaient l'adresse mémoire de l'opérande à utiliser, et les bits 13 à 15 spécifiaient l'opération à exécuter, comme enregistrer un nombre en mémoire ; les 16 autres bits étaient inutilisés[24]. L'architecture de la SSEM était « à accumulateur », ce qui signifie que l'accumulateur pouvait représenter un second opérande implicite pour les opérations arithmétiques. Pour les instructions de rupture de séquence (saut inconditionnel relatif), le compteur programme correspondait, également, à un opérande implicite. Dans tous les cas, les instructions de programmes n'indiquaient qu'un seul opérande, via son adresse en mémoire, les autres opérandes (s'ils étaient nécessaires) étaient implicites : la machine SSEM possédait une architecture dite à une seule adresse.

Un mot dans la mémoire de l'ordinateur pouvait être lu, écrit, ou rafraîchi en 360 microsecondes. Une instruction prenait quatre fois plus de temps pour s'exécuter qu'il n'en fallait pour lire un mot en mémoire, ce qui donnait une vitesse d'exécution d'environ 700 instructions par seconde. La mémoire vive était rafraîchie continuellement, ce qui prenait 20 millisecondes car il fallait lire puis rafraîchir chacun des 32 mots de la SSEM en séquence[20].

La SSEM représentait les nombres négatifs par leur complément à deux[25], comme la plupart des ordinateurs le font toujours. Dans cette représentation, la valeur du bit de poids fort dénote le signe du nombre : il vaut 0 pour les nombres positifs et 1 pour les nombres négatifs. Donc, l'intervalle de nombres que l'on pouvait représenter dans chaque mot allait de −231 à +231−1, soit de −2,147,483,648 à +2,147,483,647.

Programmation

Jeu d'instructions

Le jeu d'instructions à 3 bits de la SSEM permettait un maximum de 8 (23) instructions distinctes. Au contraire des conventions modernes, la mémoire de la machine était disposée avec les bits de poids faible à gauche ; le nombre 1 était donc représenté par « 100 », au lieu de « 001 », qui serait plus habituel[25].

Jeu d'instructions de la SSEM[26]
Code binaire Notation originale Mnémonique moderne Opération
000 S, Cl JMP S Branchement vers l'instruction à l'adresse obtenue à l'adresse S indiquée[t 1] (saut inconditionnel absolu)
100 Add S, Cl JRP S Branchement vers l'instruction à l'adresse correspondant au compteur programme plus (+) la valeur relative obtenue à l'adresse S indiquée [t 2] (saut relatif inconditionnel)
010 -S, C LDN S Prendre le nombre à l'adresse S indiquée, calculer son opposé, et enregistrer le résultat dans l'accumulateur
110 c, S STO S Enregistrer le nombre dans l'accumulateur à l'adresse S indiquée
001 ou
101[t 3].		 SUB S SUB S Soustraire le nombre à l'adresse S indiquée de la valeur de l'accumulateur et enregistrer le résultat dans l'accumulateur
011 Test CMP Sauter l'instruction suivante si l'accumulateur contient une valeur négative
111 STOP STP Arrêt
  1. Comme le compteur programme était incrémenté au cours du processus de décodage, l'adresse enregistrée en mémoire devait correspondre à l'adresse visée - 1.
  2. Comme le compteur programme était incrémenté au cours du processus de décodage, la valeur enregistrée en mémoire devait correspondre à l'adresse visée - PC - 1.
  3. Les bits représentant l'instruction n'étaient que partiellement décodés, pour économiser des éléments logiques[26]

La présence d'opposé dans certaines opérations était une conséquence du manque de matériel dans la SSEM pour effectuer toute autre opération que la soustraction et l'opposé. La construction d'un additionneur ne fut pas considérée comme nécessaire avant le début des essais, car l'addition peut facilement être réalisée par la soustraction[24]. Par exemple, x+y peut se calculer par −(−x−y). L'addition de deux nombres nécessitait donc quatre instructions[26]. Le code suivant réalise ce calcul.

LDN X // charge −X dans l'accumulateur
SUB Y // retranche Y de la valeur de l'accumulateur
STO S // enregistre le résultat dans S
LDN S // charge −S dans l'accumulateur

Les programmes étaient chargés sous forme binaire en parcourant tous les mots de la mémoire en séquence et en utilisant un ensemble de 32 interrupteurs, qui servaient de périphérique d'entrée, pour positionner la valeur de chaque bit de chaque mot à 0 ou 1. La SSEM n'avait pas de lecteur de carte ou ruban perforé[20].

Premiers programmes
L'écran de sortie

Trois programmes furent écrits pour l'ordinateur. Le premier, qui consistait en 17 instructions, fut écrit par Kilburn et fonctionna le [27]. Il était conçu pour trouver le plus grand facteur propre de 218 (262 144) en essayant tous les entiers à partir de 218−1 dans l'ordre décroissant. Les divisions étaient réalisées par des soustractions itérées du diviseur. La SSEM prit 3,5 millions d'opérations et 52 minutes pour trouver la solution (131 072). Le programme utilisait 8 mots de mémoire vive en plus de ses 17 mots d'instructions, ce qui donne une taille de programme de 25 mots[28].

Geoff Tootill écrivit une version modifiée du programme le mois suivant, et à la mi-juillet, Alan Turing, qui avait été nommé reader[note 1] au département de mathématiques de l'université de Manchester en , écrivit le troisième programme, qui effectuait la division longue. Turing avait, à cette époque, été nommé directeur assistant du laboratoire de machines à calculer de l'université[29], poste symbolique car le laboratoire ne devint une réalité physique qu'en 1951[30].

Suites de l'expérience
Une plaque en l'honneur de Williams et Kilburn à l'université de Manchester

Williams et Kilburn décrivirent la SSEM dans une lettre publiée par le journal Nature en [31].

Manchester Mark I et Ferranti Mark I

La démonstration de la viabilité de la machine conduisit rapidement à la construction d'un ordinateur plus utile en pratique, le Manchester Mark I, sur lequel le travail commença en . Cette machine fut la première de l'histoire à contenir des registres d'index, qui permettaient de modifier le comportement des instructions. Elle avait plus de mémoire, avec 64 mots de 40 bits auxquels s'ajoutait un tambour magnétique contenant 1 024 mots, et possédait un jeu d'instructions complet, avec notamment un multiplieur matériel. La première version fut opérationnelle en [30] et, à son tour, mena directement au développement du Ferranti Mark I, le premier ordinateur généraliste commercialisé au monde[3].

Reconstruction

En 1998, une réplique fonctionnelle de la SSEM, à présent exposée au musée des sciences et de l'industrie de Manchester, fut construite pour célébrer le 50e anniversaire de l'exécution de son premier programme. Des démonstrations de la machine en marche ont régulièrement lieu au musée[32]. En 2008, une photographie panoramique originale de la machine entière fut découverte à l'université de Manchester. La photographie, prise le par un étudiant en stage de recherche, Alec Robinson, avait été reproduite dans l'Illustrated London News en [33],[34].

Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Manchester Small-Scale Experimental Machine » (voir la liste des auteurs).

Notes
  1. Le rang de reader est spécifique au Royaume-Uni. Il est à peu près équivalent, dans le système anglo-saxon, à celui de professeur assistant avec tenure.

Références
  1. (en) Nicholas Enticknap, « Computing's Golden Jubilee », Resurrection, The Computer Conservation Society, no 20,‎ (ISSN 0958-7403, lire en ligne)
  2. (en) « Early Electronic Computers (1946–51) », University of Manchester (consulté le )
  3. (en) R.B.E. Napper, « Introduction to the Mark 1 », The University of Manchester (consulté le )
  4. Turing 1937
  5. (en) « Z3 », Université technique de Berlin
  6. (en) Horst Zuse, « The Life and Work of Konrad Zuse, Part 2: Konrad Zuse's First Ideas on Computing », Everyday Practical Electronics (consulté le )
  7. Lavington 1998, p. 7
  8. Lavington 1998, p. 1
  9. Brown 1999, p. 429
  10. Lavington 1998, p. 9
  11. Lavington 1980, Chapitre 5: ACE, the 'British National Computer'
  12. Lavington 1998, p. 8–9
  13. Lavington 1998, p. 5
  14. (en) « How did CSIRAC work?: Storage », Université de Melbourne, 4& avril 2006 (consulté le )
  15. (en) « Early computers at Manchester University », Resurrection, The Computer Conservation Society, vol. 1, no 4,‎ (ISSN 0958-7403, lire en ligne)
  16. Lavington 1998, p. 13
  17. Lavington 1998, p. 24
  18. Lavington 1998, p. 12
  19. Lavington 1998, p. 12–13
  20. Napper 2000, p. 366
  21. Lavington 1998, p. 16
  22. Lavington 1998, p. 6–7
  23. (en) [PDF] « The "Baby": The World's First Stored-Program Computer », Manchester Museum of Science & Industry (consulté le )
  24. Napper 2000, p. 367
  25. Lavington 1998, p. 14
  26. Lavington 1998, p. 15
  27. (en) Christopher P. Burton, « Rebuilding the First Manchester Computer », The First Computers — History and Architectures, MIT Press,‎ , p. 379-386 (ISBN 978-0-262-18197-6)
    Partiellement disponible en ligne
  28. (en) Geoff Tootill, « The Original Original Program », Resurrection, The Computer Conservation Society, no 20,‎ (ISSN 0958-7403, lire en ligne)
  29. Lavington 1998, p. 16–17
  30. Lavington 1998, p. 17
  31. « Electronic Digital Computers », Nature, vol. 162,‎ , p. 487 (lire en ligne)
  32. (en) « Meet Baby », Manchester Museum of Science & Industry (consulté le )
  33. (en) Roger Highfield, « Photo of great grandfather of modern computers found », Daily Telegraph,‎ (lire en ligne)
  34. (en) « Panoramic image of SSEM and other audiovisual records (Digital 60, University of Manchester) » (consulté le )

Annexes

Bibliographie
  • (en) Louis Brown, A Radar History of World War II : Technical and Military Imperatives, CRC Press, , 563 p. (ISBN 978-0-7503-0659-1)
  • (en) Simon Lavington, Early British Computers : The Story of Vintage Computers and the People who built them, Swindon, Manchester University Press Society, , 1re éd. (ISBN 0-7190-0803-4)
  • (en) Simon Lavington, A History of Manchester Computers, Swindon, The British Computer Society, , 2e éd. (ISBN 1-902505-01-8)
  • (en) R. B. E. Napper, Raúl Rojas (dir.) et Ulf Hashagen (dir.), The First Computers: History and Architectures, MIT Press, (ISBN 0-262-68137-4, lire en ligne), p. 356–377
  • (en) Alan Turing, On Computable Numbers, with an Application to the Entscheidungsproblem : Proceedings of the London Mathematical Society, London Mathematical Society, (DOI 10.1112/PLMS/S2-42.1.230, lire en ligne) et « [idem] : A Correction », Proc. London Math. Soc., 2e série, vol. 43,‎ , p. 544-546 (DOI 10.1112/plms/s2-43.6.544, lire en ligne)

Articles connexes

Liens externes
  • Portail de l’informatique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.