Superparamagnétisme

Lorsque les dimensions d'une particule atteignent l'échelle du nanomètre, les effets de la température et du temps sur le moment de la particule deviennent cruciaux. Louis Néel a dévoilé ces effets. Cette découverte l'a conduit aux notions très importantes de superparamagnétisme et de température de blocage. L'expression du temps de relaxation en fonction du champ appliqué, donnée par Néel dès 1949[1], est connue sous le nom de loi de Néel-Brown. Malgré son importance et les expérimentations effectuées depuis une cinquantaine d'années, cette loi n'a pu être vérifiée que très récemment.

En principe, n’importe quel matériau ferromagnétique ou ferrimagnétique subit une transition vers un état paramagnétique au-dessus de sa température de Curie. Le superparamagnétisme apparaît en dessous de la température de Curie du matériau, alors que le matériau est dans l'état ferromagnétique. Le superparamagnétisme est relatif à des grains qui sont mono-domaines, c’est-à-dire composés d’un seul domaine magnétique. La taille en dessous de laquelle des grains magnétiques sont dits monodomaines dépend du matériau. Elle est de l'ordre de la dizaine/centaine de nanomètres. Dans ces conditions, on peut considérer que l’aimantation du grain est en fait un seul moment magnétique géant, somme de tous les moments magnétiques portés par le grain. On parle d’"approximation macro-spin".

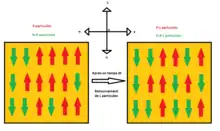
A cause de l'anisotropie magnétique des grains, le moment magnétique a généralement deux orientations stables. Elles sont antiparallèles l'une par rapport à l'autre et séparées par une barrière d'énergie. Ces orientations stables sont appelées « axes de facile aimantation » du grain. A une température donnée, il y a une probabilité non nulle que l’aimantation du grain (i.e. le macro-spin) se retourne complètement (rotation de ${\displaystyle 180^{\circ }}$). Le temps moyen entre deux renversements est appelé le temps de relaxation de Néel ${\displaystyle \tau _{N}}$ et est donné par l’équation d'Arrhenius suivante :

${\displaystyle \tau _{N}=\tau _{0}e^{\left({\frac {KV}{k_{B}T}}\right)}}$

Retournement de l'aimantation d'un grain au bout d'un temps τ.

où :

• ${\displaystyle \tau _{N}}$ est le temps moyen entre deux retournements de l'aimantation du grain ;
• ${\displaystyle \tau _{0}}$ est un temps d'essai, d'une valeur comprise entre 10^-9 et 10^-10 secondes ;
• K est l’anisotropie magnétique du grain et V son volume. On peut alors considérer que KV est l’énergie de barrière associée au retournement de l’aimantation qui, partant de son axe facile initial, passe par un axe difficile, puis revient sur un autre axe facile ;
• k_B est la constante de Boltzmann ;
• T est la température.

Eléments de démonstration de la loi d'Arrhenius

Il est question ici de développer la philosophie générale de la démonstration de la loi d'Arhénius. Pour connaître la démonstration précise et complète, le lecteur pourra se référer à des ouvrages dédiés à ce but [J. L. Dormann, « Le phénomène de superparamagnétisme ». Pour commencer, on considère un système avec N particules dont P particules ont leur moment magnétique orienté selon la direction (Oz) et N-P particules de moment magnétique opposé, à savoir -(Oz).

Variation dans le temps de l'orientation de l'aimantation d'un nombre L d'atomes (Réalisé via Paint).

Au cours d'un intervalle de temps dt, un certain nombre (noté L sur l'image précédente) de particules a son moment magnétique qui s'inverse. Ainsi, l'équation de variation temporelle du nombre de particules dont l'orientation de l'aimantation est orientée selon (Oz) est :

${\displaystyle {\frac {dP}{dt}}={\frac {N-P}{2\tau }}+{\frac {P}{2\tau }}}$

Avec ${\displaystyle \tau }$ qui est la durée du retournement de l'aimantation de la particule. Il dépend donc du nombre de particules dont le moment magnétique s'inverse au cours de ce lapse de temps. Comme on peut le voir sur l'animation, Retournement de l'aimantation d'un grain au bout d'un temps τ, ce retournement ne se fait pas sans le franchissement d'une barrière énergétique. Il est donc indispensable que de l'énergie soit fournie à la particule pour que son aimantation se retourne. Cette énergie est l'énergie thermique du réseau qui se retrouve dans le terme ${\displaystyle \Gamma }$, ce terme correspondant à la moyenne des forces (ou couples) permettant d'orienter l'aimantation de la particule selon l'axe (Oz). En faisant l'analogie avec un système gyroscopique, l'expression de ${\displaystyle \tau }$ est:

${\displaystyle {\frac {1}{\tau }}=E_{B}{\frac {eg}{mkT}}{\frac {\Gamma }{m_{S}}}exp(-{\frac {E_{B}}{kT}})}$

Avec:

• ${\displaystyle g}$, le facteur de Landé ;
• ${\displaystyle e}$, la charge de l'électron ;
• ${\displaystyle E_{B}}$, l'énergie de Boltzmann ;
• ${\displaystyle m_{S}}$, le champ démagnétisant ;
• ${\displaystyle \Gamma }$, la moyenne des forces (ou couples) permettant d'orienter l'aimantation de la particule selon l'axe (Oz). Ce terme s'exprime en fonction de l'énergie magnéto-élastique et du champ démagnétisant.

Le premier terme peut être reformulé par une constante, soit:

${\displaystyle {\frac {1}{\tau }}=2Aexp(-{\frac {E_{B}}{kT}})}$

Ce temps de relaxation peut valoir de quelques nanosecondes à plusieurs années (voire plus). En particulier, on peut constater qu’il varie exponentiellement avec le volume du grain, ce qui explique pourquoi cette probabilité de saut est négligeable pour des matériaux massifs ou comportant de gros grains.

Imaginons que l’on mesure l’aimantation d’un seul grain superparamagnétique et appelons ${\displaystyle \tau _{m}}$ le temps que prend cette mesure. Si ${\displaystyle \tau _{m}}$ >> ${\displaystyle \tau _{N}}$, l’aimantation du grain se retourne de nombreuses fois pendant la mesure. L’aimantation mesurée apparaît nulle. Si ${\displaystyle \tau _{m}}$ << ${\displaystyle \tau _{N}}$, son aimantation ne se retourne pas pendant la mesure. L'aimantation mesurée est le moment magnétique porté par le grain. Dans le premier cas, le grain sera dit dans un état superparamagnétique et dans le second dans l’état ferromagnétique, ou bloqué. L’état de la particule pour l’observateur (superparamagnétique ou ferromagnétique) dépend donc du temps de mesure. Une transition entre état superparamagnétique et état ferromagnétique a lieu lorsque ${\displaystyle \tau _{m}}$ = ${\displaystyle \tau _{N}}$. Dans de nombreuses expériences, le temps de mesure de l’aimantation est constant, mais la température varie, de telle sorte que la transition ferromagnétique-superparamagnétique est observée à une certaine température. La température pour laquelle ${\displaystyle \tau _{m}}$ = ${\displaystyle \tau _{N}}$ est appelée température de blocage car, en dessous de cette température, l’aimantation du grain est vue comme « bloquée » à l’échelle du temps de mesure.

${\displaystyle T_{B}={\frac {KV}{k_{B}\ln \left({\frac {\tau _{m}}{\tau _{0}}}\right)}}}$

Dans une assemblée de N grains, l’application d’un champ magnétique extérieur tend à faire s’aligner les grains superparamagnétiques le long du champ. La courbe d'aimantation de l'ensemble est une fonction réversible croissante ayant la forme d'un "S". Cette fonction est généralement compliquée, sauf dans deux cas :

1. Si toutes les particules sont identiques (même barrière d'énergie et même moment magnétique), leurs axes de facile aimantation sont tous orientés parallèlement au champ appliqué, et si la température est assez basse (T ≲ KV/(10 k_B)), alors l'aimantation de l'assemblée est:
   ${\displaystyle M(H)\approx N\mu \tanh \left({\frac {\mu _{0}H\mu }{k_{B}T}}\right)}$.
2. Si toutes les particules sont identiques et que la température est assez élevée (T ≳ KV/k_B), alors quelle que soit l'orientation des axes faciles:
   ${\displaystyle M(H)\approx N\mu L\left({\frac {\mu _{0}H\mu }{k_{B}T}}\right)}$

Alignement de l'aimantation des grains superparamagnétiques suite à l'application d'un champ magnétique externe.

Dans les équations ci-dessus :

• ${\displaystyle \mu _{0}}$ est la perméabilité magnétique dans le vide ;
• ${\displaystyle \mu }$ est le moment magnétique de la nanoparticule ;
• ${\displaystyle \mu _{0}H}$ correspond au champ magnétique appliqué ;
• ${\displaystyle L(x)=\coth(x)-{\frac {1}{x}}}$ est la fonction de Langevin ;

La pente ${\displaystyle {\frac {\partial M}{\partial H}}}$ à l'origine de la fonction ${\displaystyle M(H)}$ est la susceptibilité magnétique ${\displaystyle \chi }$ des grains :

${\displaystyle \chi ={\frac {N\mu _{0}\mu ^{2}}{k_{B}T}}}$ dans le premier cas

${\displaystyle \chi ={\frac {N\mu _{0}\mu ^{2}}{3k_{B}T}}}$ dans le second cas.

Cette susceptibilité est aussi valable pour des températures supérieures à la température de blocage si les axes faciles de la nanoparticule sont orientés de manière aléatoire.

On peut constater d’après cette expression que les grains les plus gros, portant donc un large µ, ont une susceptibilité plus forte. Ceci explique pourquoi les grains superparamagnétiques ont une susceptibilité plus forte que les matériaux paramagnétiques standard : ils se comportent exactement comme des moments paramagnétiques géants.

• J. L. Dormann, « Le phénomène de superparamagnétisme », dans Revue de Physique Appliquée, vol. 16, n^o 6, juin 1981, p. 275-301 [PDF].
• Bernard Barbara, « L'œuvre de Louis Néel », sur louisneel-centenaire.inpg.fr, CNRS, 2001 (consulté le 6 octobre 2012), p. 7/10 [PDF].
• Michel Prévot, David Dunlop, « Louis Néel : quarante ans de magnétisme », sur hal.archives-ouvertes.fr (consulté le 9 octobre 2012), p. 2/4 [PDF].
• Florent Tournus, "Magnetic properties of nanoparticles : from individual objects to cluster assembles", Institut Lumière Matière (ILM), p. 42-45 [PDF].
• Miha Maroit, "Superparamagnetic Materials", Université de Ljubljana, Faculté de Mathématiques et de Sciences Physiques, avril 2014, p. 1-4 [PDF].
• Arnauld Hillion, "Étude des propriétés magnétiques d’assemblées de nanoparticules de Co, FeRh et FeAu", Université Claude Bernard - Lyon 1, octobre 2012, [PDF].
• Oscar Cubero, "Travaux pratiques débutants TPD Expérience n°31 Cycle d'hystérésis", p 2-3.

• Portail de la physique