Test de planarité gauche-droite

En théorie des graphes, et en algorithmique, le test de planarité gauche-droite, aussi appelé critère de planarité de Fraysseix-Rosenstiehl[1] est une caractérisation des graphes planaires basée sur les propriétés des arbres de parcours en profondeur ou arbres de Trémaux, publiée par de Fraysseix et Rosenstiehl en 1982 et 1985[2],[3], et utilisée par eux, avec Patrice Ossona de Mendez, pour développer un algorithme de test de planarité en temps linéaire[4],[5]. Dans une comparaison pratique de six algorithmes de test de planarité réalisée en 2003[6] , il s'agissait alors de l'un des algorithmes testés les plus rapides.

Arêtes similaires et opposées

Dans toute recherche en profondeur d'un graphe G, les arêtes rencontrées lors de la découverte d'un sommet pour la première fois définissent un arbre de recherche en profondeur T de G. Un tel arbre est aussi appelé un arbre de Trémaux ; les arêtes restantes, qui constituent par définition le coarbre, relient chacune une paire de sommets qui sont ancêtre ou descendant l'un de l'autre dans T.

Deux arêtes du coarbre sont appelées similaires si elles figurent du même côté dans T, elles sont opposées dans le cas contraire. Dans les figures suivantes, les cercles simples représentent les sommets, les cercles doubles représentent les sous-arbres, les segments torsadés représentent les chemins des arbres et les arcs courbes représentent les arêtes du coarbre. La racine de chaque arbre figure au bas de la figure. Dans la première figure, les arêtes étiquetés et sont similaires pour T, ce qui signifie qu'aux extrémités les plus proches de la racine de l'arbre, elles seront toutes les deux du même côté de l'arbre dans tout dessin dans le plan. Dans les deux figures suivantes, les arêtes avec les mêmes étiquettes sont opposées pour T, ce qui signifie qu'elles se trouveront sur des côtés opposés de l'arbre dans chaque dessin dans le plan.

et sont similaires
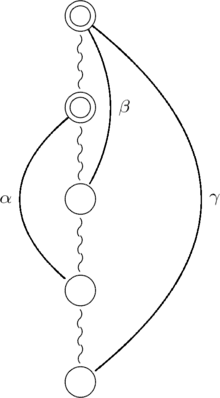et sont opposés
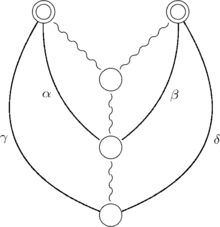et sont opposés

Caractérisation

Théorème — Soit G un graphe et soit T un arbre de Trémaux de G. Le graphe G est planaire si et seulement s'il existe une partition des arêtes du coarbre de G en deux classes, de sorte que deux arêtes appartiennent à une même classe si elles sont du même côté de T et que deux arêtes appartiennent à des classes différentes si elles sont du côté opposé de T.

Cette caractérisation conduit immédiatement à un test de planarité (mais qui est inefficace dans cette formulation) : on détermine, pour toutes les paires d'arêtes si elles sont du même côté ou de côtés opposés, on forme ensuite un graphe auxiliaire qui a un sommet pour chaque composante connexe formé d'arêtes similaires et une arête pour chaque paire d'arêtes opposées ; ce graphe auxiliaire doit être biparti. Rendre cet algorithme efficace consiste à trouver un sous-ensemble des paires similaires et opposés qui suffit pour effectuer cet algorithme sans devoir déterminer la relation entre toutes les paires d'arêtes du graphe donné.

Références
  1. Christopher Auer, Andreas Gleißner, Kathrin Hanauer et Sebastian Vetter, « Testing planarity by switching trains », Graph Drawing: 20th International Symposium, GD 2012, Redmond, WA, USA, September 19-21, 2012, Revised Selected Papers, Berlin, Springer, vol. 7704,‎ , p. 557–558 (DOI 10.1007/978-3-642-36763-2_51).
  2. Hubert de Fraysseix et Pierre Rosenstiehl, « A depth-first-search characterization of planarity », Graph Theory (Cambridge, 1981), North-Holland, Amsterdam-New York,‎ , p. 75–80 (Math Reviews 671906).
  3. Hubert de Fraysseix et Pierre Rosenstiehl, « A characterization of planar graphs by Trémaux orders », Combinatorica, vol. 5, no 2,‎ , p. 127–135 (DOI 10.1007/BF02579375, Math Reviews 815578).
  4. Hubert de Fraysseix, Patrice Ossona de Mendez et Pierre Rosenstiehl, « Trémaux trees and planarity », International Journal of Foundations of Computer Science, vol. 17, no 5,‎ , p. 1017–1029 (DOI 10.1142/S0129054106004248, Math Reviews 2270949, arXiv math.CO/0610935).
  5. Hubert de Fraysseix et Patrice Ossona de Mendez, « Trémaux trees and planarity », European Journal of Combinatorics, vol. 33, no 3,‎ , p. 279–293 (DOI 10.1016/j.ejc.2011.09.012, Math Reviews 2864415, arXiv math/0610935).
  6. John M. Boyer, Pier Francesco Cortese, Maurizio Patrignani et Giuseppe Di Battista, « Stop minding your P's and Q's: implementing a fast and simple DFS-based planarity testing and embedding algorithm », Graph Drawing: 11th International Symposium, GD 2003 Perugia, Italy, September 21-24, 2003, Revised Papers, Berlin, Springer,‎ , p. 25–36 (DOI 10.1007/978-3-540-24595-7_3, Math Reviews 2177580).

Bibliographie complémentaire
  • (de) Daniel Kaiser, Implementation und Animation des Links-Rechts-Planaritätstests : Bachelorarbeit, (Diplomarbeit) Université de Constance, FB Informatik und Informationswissenschaft, .

Article lié
  • Portail des mathématiques
  • Portail de l'informatique théorique
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.