Théorème d'Hoffman-Singleton
Le théorème d'Hoffman-Singleton est un théorème de théorie des graphes, prouvé en 1960 par Alan Hoffman et Robert Singleton. Ce théorème établit que tout graphe de Moore de diamètre 2 ne peut avoir qu'un degré égal à 2, 3, 7 ou 57.
Exemples de graphes de Moore
 Le pentagone est un graphe de Moore à 5 sommets ().
Le pentagone est un graphe de Moore à 5 sommets ().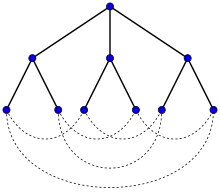 Le graphe de Petersen est un graphe de Moore à 10 sommets ().
Le graphe de Petersen est un graphe de Moore à 10 sommets ().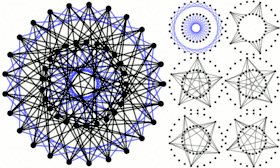 Le graphe de Hoffman-Singleton est un graphe de Moore à 50 sommets ().
Le graphe de Hoffman-Singleton est un graphe de Moore à 50 sommets ().
L'existence d'un graphe de Moore de diamètre 2 de degré possédant 3250 sommets est encore un problème ouvert.
Formulation algébrique
Théorème — Soit une matrice symétrique à coefficients 0 ou 1 de trace nulle. S'il existe vérifiant :
alors .
Voir aussi
Article connexe
Référence
Sujet ENS 1986 section A1 épreuve de MATH.2
Lien externe
(en) Eric W. Weisstein, « Hoffman-Singleton Theorem », sur MathWorld
- Portail des mathématiques
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.