Théorème de Pitot
En géométrie, le théorème de Pitot, démontré en 1725[1] par l'ingénieur français Henri Pitot[2], énonce que si un quadrilatère est circonscriptible (c'est-à-dire si ses quatre côtés sont tangents à un même cercle), alors la somme des longueurs de deux côtés opposés est égale à la somme des deux autres.
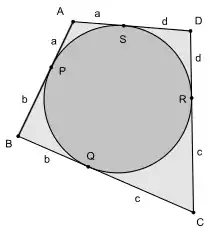
AB + CD = (a + b) + (c + d) =
(a + d) + (b + c) = AD + BC.
(a + d) + (b + c) = AD + BC.
Pour le démontrer, il suffit de décomposer ces quatre longueurs, selon les points de tangence, en huit longueurs égales deux à deux. Pitot démontra la propriété analogue pour un polygone circonscriptible à un nombre pair de sommets, et l'étendit à un nombre impair de sommets.
La réciproque fut démontrée par Jakob Steiner en 1846.
Notes et références
- Pierre Humbert, « L'œuvre mathématique d'Henri Pitot », Revue d'histoire des sciences et de leurs applications, no 6, , p. 322-328 (lire en ligne [PDF], consulté le )
- Henri Pitot, « Propriétés élémentaires des polygones circonscrits autour du cercle », Histoire de l'Académie royale des sciences avec les mémoires de mathématique et de physique tirés des registres de cette Académie, , p. 45-47 (lire en ligne [PDF], consulté le ).
- Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.