Théorème de Stewart

En géométrie euclidienne, le théorème de Stewart est une généralisation du théorème de la médiane due au mathématicien Matthew Stewart en 1746[1].

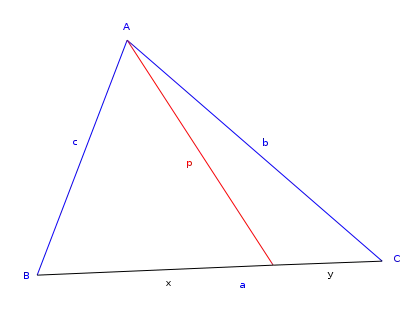
Illustration du théorème de Stewart

Énoncé

Théorème — Soit $p$ une cévienne d'un triangle $ABC$ divisant en $X$ le côté $a$ en deux parties $x$ et $y$ . On a alors la "relation de Stewart":

a\cdot (xy+p^{2})=x\cdot b^{2}+y\cdot c^{2}

Démonstration

D'après le théorème d'Al-Kashi, on a :

\cos({\widehat {BXA}})={\frac {x^{2}+p^{2}-c^{2}}{2xp}},\ \cos({\widehat {CXA)}}={\frac {y^{2}+p^{2}-b^{2}}{2yp}}

Puisque ${\widehat {BXA}}$ et ${\widehat {CXA}}$ sont supplémentaires, alors la somme de leurs cosinus est nulle, d'où, successivement :

{\begin{aligned}{\frac {x^{2}+p^{2}-c^{2}}{2xp}}+{\frac {y^{2}+p^{2}-b^{2}}{2yp}}&=0\\2yp\cdot (x^{2}+p^{2}-c^{2})+2xp\cdot (y^{2}+p^{2}-b^{2})&=0\\2ypx^{2}+2yp^{3}+2xpy^{2}+2xp^{3}&=2ypc^{2}+2xpb^{2}\\x^{2}y+yp^{2}+xy^{2}+xp^{2}&=yc^{2}+xb^{2}\\a\cdot (xy+p^{2})&=yc^{2}+xb^{2}\end{aligned}}

Autre formulation

Étant donnés une droite orientée comportant trois points $A,B,C$ et un point $M$ , la relation de Stewart s'écrit[2]:

{MA}^{2}\cdot {\overline {BC}}+{MB}^{2}\cdot {\overline {CA}}+{MC}^{2}\cdot {\overline {AB}}+{\overline {AB}}\cdot {\overline {BC}}\cdot {\overline {CA}}=0

Voir aussi

Le théorème de Holditch, qui en constitue une généralisation.

Lien externe

(en) Eric W. Weisstein, « Stewart's Theorem », sur MathWorld

Références

(en) Matthew Stewart, « Some General Theorems of Considerable Use in the Higher Parts of Mathematics », Edinburgh: Sands, Murray and Cochran,‎ 1746, Proposition II
F. Brachet et J. Dumarqué, Précis de géométrie : Compléments, Transformations, Coniques, Librairie Delagrave, 1939, Révisions et compléments, chap. V (« Relations métriques »).

Portail de la géométrie

Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.

[1] (en) Matthew Stewart, « Some General Theorems of Considerable Use in the Higher Parts of Mathematics », Edinburgh: Sands, Murray and Cochran,‎ 1746, Proposition II

[2] F. Brachet et J. Dumarqué, Précis de géométrie : Compléments, Transformations, Coniques, Librairie Delagrave, 1939, Révisions et compléments, chap. V (« Relations métriques »).