Théorème de la porte


Le théorème de la porte est un théorème de géométrie dans l'espace.

Le nom de théorème de la porte lui est parfois donné[1],[2], [3] car cette propriété est utile aux menuisiers pour s'assurer que l'axe de rotation d'une porte est perpendiculaire au plancher.

Énoncé et illustration

Théorème de la porte — Si une droite est orthogonale à deux droites sécantes du plan alors elle est orthogonale à toutes les droites du plan. On dit alors que la droite est perpendiculaire au plan.

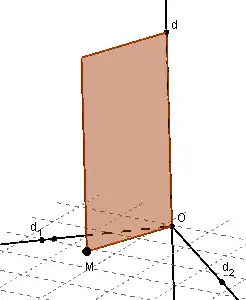
Propriété du menuisier : la droite (d), perpendiculaire aux droites (d1) et (d2) sécantes en O, est perpendiculaire au plan (p) contenant ces deux droites. La porte tourne alors normalement autour de (d)[4].

Cette propriété de géométrie dans l'espace se révèle tellement utile qu'on lui donne parfois le nom de théorème fondamental de l'orthogonalité[4].

Elle se démontre facilement à l'aide du produit scalaire[5]. Mais Daniel Perrin[6] propose une démonstration utilisant uniquement des triangles isométriques: partant d'une droite (d) perpendiculaire en O à deux droites sécantes (d1) et (d2) du plan, il démontre qu'elle est perpendiculaire à toute autre droite (d3) du plan passant par O. Pour ce faire, il envisage une droite du plan coupant les trois droites en A, B et C, prend sur (d) deux points M et N symétriques par rapport à O et travaille successivement sur les triangles isométriques MAB et NAB puis MAC et NAC pour démontrer que (d3) est médiatrice de [MN].

C'est une méthode utile pour démontrer que deux droites sont orthogonales : il suffit de démontrer qu'une des droites est perpendiculaire à un plan contenant l'autre droite[7], ou plus simplement que cette droite est orthogonale à deux droites sécantes d'un plan contenant l'autre droite. En particulier, ce théorème permet de démontrer le théorème des trois perpendiculaires[7].

Article connexe

Théorème du toit

Notes et références
  1. Règles de bases en géométrie de l'espace
  2. Géométrie dans l'espace - Cours de première
  3. T. Joffredo, Memento de classe de première
  4. Collection Terracher, Math Seconde, Hachette Édition, 1994, p. 253
  5. Voir par exemple, Daniel Perrin, Droite et plan de l'espace pour exposé de Capes, p. 13
  6. Daniel Perrin, Mathématiques d'école - Nombres, mesures et géométrie, Édition Cassini, 2011, p. 274
  7. André Deledicq, Maths Lycée Éditions de la cité, 1998, pp 220-221
  • Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.