Tobias Mayer
Tobias[1] Mayer (né le à Marbach am Neckar (duché de Wurtemberg) et mort le à Göttingen) est un mathématicien, cartographe et astronome allemand. Autodidacte, il est devenu un scientifique reconnu ; il n'a jamais étudié à l'université, mais il y a enseigné.
Pour les articles homonymes, voir Mayer.

| Naissance | |
|---|---|
| Décès | |
| Activités | |
| Enfant |
Johann Tobias Mayer (en) |
| A travaillé pour |
|---|
Biographie
La vie de Tobias Mayer s'est déroulée dans quatre villes : Esslingen, Augsburg, Nuremberg et Göttingen.
Esslingen (1724 ou 1725–1744)
Il grandit dans un milieu modeste à Esslingen am Neckar, où la famille est déménagée quand il avait à peu près deux ans[2]. Son père (1682-1731) s'appelle également Tobias et est fontainier. De 1729 à 1741, il va à l’école locale et à l’école latine[3] à Esslingen. Comme les mathématiques ne sont pas enseignées dans cette école, Tobias se forme en autodidacte. Après la mort de son père en 1731, il est hébergé à l’orphelinat. En raison de ses aptitudes, il est encouragé pendant quelque temps par le maire d’Esslingen. À la mort de ce protecteur, Tobias passe sous l'aile d'un cordonnier avide de savoir : « Nous nous arrangions bien mon cordonnier et moi ; […] il avait de l'argent pour acheter des livres, mais pas de temps pour les lire : il fallait qu'il fasse des souliers. Moi, j'avais le temps de lire, mais pas d'argent pour acheter des livres. » Le soir, Tobias fait un résumé de ses lectures pour le cordonnier[4],[5].
Sa mère meurt en 1737. En 1739, il publie le premier plan de la ville d’Esslingen[6],[7] et en 1741 un livre de géométrie et de mathématiques.
Augsburg (1744–1746) et Nuremberg (1746–1751)
En 1744, après plusieurs tentatives très décevantes pour sortir de sa petite ville, il arrive à Augsbourg[8]. En 1745 il fait paraître l’« Atlas mathématique » et un livre sur l’art des constructions militaires. En 1746, quand il obtient une place dans la maison de cartographie Johann Baptist Homann à Nuremberg, il a déjà publié deux travaux originaux de géométrie. Il décèle des inexactitudes dans les cartes alors utilisées en faisant chevaucher deux cartes connues et fait la preuve d’importantes différences, surtout dans la direction est-ouest. La mesure de la longitude d’une ville était alors seulement possible avec une incertitude importante.
Göttingen (1752–1762)
En 1751, il épouse Maria Victoria, née Gnüg (1723–1780), fille de pasteur[9],[10], et, l’année suivante, naît son fils Johann Tobias (en), qui sera physicien comme son père[1].
En raison de ses apports dans le domaine de la cartographie et, vu sa réputation de scientifique, il est nommé, en 1751 également, à la chaire d’économie et de mathématiques de l’université de Göttingen[11].
De 1752 à 1756, il fait paraître des publications sur la détermination de la longitude, l’astronomie, la géophysique, les mathématiques et les instruments de mesure. Dans les années 1757–1762, il publie, malgré la Guerre de Sept ans, d’autres travaux d’astronomie et écrit aussi sur le champ magnétique terrestre et la théorie des couleurs.
En 1754, il devient directeur du nouvel observatoire de Göttingen, qui est hébergé dans une tour des remparts de la ville. Il y travaille avec beaucoup d’enthousiasme et de succès, jusqu’à ce qu’il meure du typhus en 1762. Sur son lit de mort, l'« immortel Mayer », comme le désigne Carl Friedrich Gauß[12], demande à Maria Victoria d'aller en Angleterre non seulement avec ses propres tables, mais aussi avec les observations de son ancien élève Carsten Niebuhr[13].
Contributions
Astronomie
L'article de Tobias Mayer paru dans Kosmographische Nachrichten en 1750 est une étude minutieuse de la libration lunaire. Ses cartes de la Lune (40 en tout), publiées par Lichtenberg en 1775 à titre posthume, ne seront pas dépassées durant un demi-siècle. Mais la renommée de Tobias Mayer repose principalement sur ses Tables de la Lune (Tabulæ motuum Solis et Lunæ novæ et correctæ), qui furent imprimées la première fois en 1752. En 1755, il remet au gouvernement anglais une version enrichie de ses Tables. La position de la Lune peut être déterminée avec une précision exceptionnelle de 75 secondes de degré et, par conséquent, la longitude en mer à 0,5 degré près. Ainsi est résolu le difficile problème de mesure de la longitude qui, jusqu’alors, a empêché une navigation sûre en haute mer. Une autre solution pour ce même problème est découverte à peu près en même temps par un horloger nommé John Harrison ; elle se fonde sur la mesure du temps au moyen de nouvelles montres qui, à bord de bateaux hauturiers à voiles, fonctionnent aussi avec une précision suffisante dans des conditions difficiles.
La théorie scientifique de Mayer, fondée sur les Tables de la Lune, est publiée à titre posthume à Londres en 1767 sous le titre Theoria Lunæ juxta systema Newtonianum (Théorie de la Lune selon le système newtonien). De même, à titre posthume, parait à Londres une version améliorée des Tables. Sa veuve apporte personnellement ces tables en Angleterre. En reconnaissance des grands mérites de Mayer dans la résolution du problème de la longitude, elle reçoit un don du gouvernement britannique de 3 000 livres. En effet, en 1714, le gouvernement britannique avait promis de récompenser par un prix de 20 000 livres la résolution de ce problème et un comité, le Board of Longitude, avait été institué à cet effet. Les cartes de la lune de Mayer sont reprises plus tard, entre autres par Johann Hieronymus Schröter.
Découverte du « cercle de réflexion »
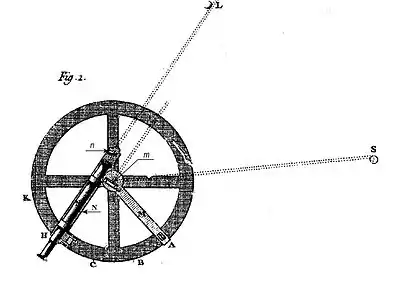
Au milieu du XVIIIe siècle apparaissent de faibles différences entre la loi universelle de la gravitation de Newton et la localisation des planètes effectivement observées. Ces différences s’élevaient pour la Lune à environ 5 minutes de degré, ce qui pouvait entraîner une incertitude de 2,5 degrés dans la détermination du degré de longitude terrestre. Selon la latitude, cela correspondait respectivement à une déclinaison et une inexactitude de navigation pouvant atteindre 150 milles nautiques. Des déterminations plus précises étant nécessaires pour l’élaboration d’une meilleure théorie du mouvement de la Lune, Tobias Mayer construit un nouvel instrument de mesure astronomique, nommé cercle de réflexion.
L’équipement, d’abord utilisé dans la mesure terrestre, est composé d’une lunette de visée qui reçoit l’image simultanée de deux objets éloignés l’un de l’autre. La première image est obtenue par vision directe et la seconde par réflexion sur deux petits miroirs. L’avantage de l’invention de Mayer est que l’angle formé par la réflexion est le double de l’angle véritable. Les défauts de lecture ou de jeu du mécanisme sont ainsi divisés par deux. En répétant l’observation une seconde fois, on divise les erreurs par quatre etc. et l’on peut arriver ainsi à une précision vingt fois plus grande qu'avant[14].

Tobias Mayer applique ce principe de répétition à un disque astronomique. On détermine la différence d’angle recherchée entre la Lune et une étoile par des mesures répétées et la division correspondante par le nombre d’opérations. Ainsi Mayer réussit, à partir de 1755, à établir ses Tables de la Lune avec une précision d’environ une minute. Plus tard, l’astronome Franz Xaver von Zach (1754–1832) décrit le disque de Mayer comme la plus importante découverte astronomique du XVIIIe siècle.
Les premiers modèles de ce nouvel appareil sont fabriqués à partir de 1750 à Göttingen et, à partir d’environ 1757, à Londres par John Bird. Rapidement, Tobias Mayer discerne que la précision qu’il peut atteindre avec l’aide d’un tel instrument pour sa théorie de la Lune permet aussi une détermination fiable de la longitude. Ainsi, seulement trois ans après la mort de Mayer, les mesures du Board of Longitude anglais montrent que la précision de la localisation en mer avec sa méthode peut être améliorée d’environ 60 milles nautiques. À partir de 1775, ces appareils, connus comme les « cercles de Borda[15] », sont optimisés et connaissent une ample diffusion (Jean-Charles de Borda a amélioré l'invention de Mayer[16]).
Solution au problème du degré de longitude
À l’exception d’un léger décalage parallactique, la Lune apparaît lors d’une observation simultanée à la même heure à la même position du ciel étoilé, également quand cette observation se fait de lieux terrestres différents. Simultanément signifie ici au même temps universel. À une date considérée, la déclinaison de la véritable heure locale, qu’on détermine par l’observation de la position du Soleil, dépend du degré de longitude de l’observateur. Comme la Lune se déplace autour de la Terre d’environ 33 minutes angulaires par heure par rapport aux étoiles fixes, on détermine par la mesure précise correspondant à l’écart d’angle entre la Lune et les étoiles fixes, la déclinaison de la véritable heure locale du temps universel, et ainsi, du degré de longitude de l’observateur, tant que des données suffisamment précises sur la position de la Lune par rapport aux étoiles fixes sont disponibles par rapport au temps universel.
On doit aussi à Tobias Mayer un catalogue de 998 étoiles zodiacales.
Psychophysique
« Dans les années 1750[17],[18], Tobias Mayer, professeur d'astronomie et de mathématiques appliquées (économie) à l'université de Göttingen, effectue deux recherches sur la psychophysique quantitative visuelle. Il en déduit que l'acuité visuelle dépend suivant une loi de puissance de l'intensité de la lumière éclairant le motif de stimulus. Ses mesures comparent l'acuité visuelle déterminée par des points noirs isolés et l'acuité visuelle mesurée par des motifs en grille ou en damier (cette dernière considérée par lui comme la « vraie » mesure de l'acuité visuelle).
Mayer développe également un espace de couleurs hexaédrique à trois dimensions à partir de la définition des mélanges soustractifs de couleurs des trois couleurs primaires (rouge, jaune, bleu). Cet espace de couleurs peut être considéré comme le prédécesseur des tables de couleurs d'Ostwald et de Munsell, qui viendront plus tard. Mayer a donné une description quantitative simple de chacune des teintes de son espace de couleurs.
Les deux études psychophysiques sont issues de l'intérêt porté par Mayer à des problèmes pratiques d'astronomie et de cartographie. »
Œuvres
Publications
- Neue und allgemeine Art, alle Aufgaben aus der Geometrie vermittelst der geometrischen Lineen leichte auzulösen — Insbesondere wie alle reguläre und irreguläre Viel-Ecke, davon eine Verhältnis ihrer Seiten gegeben, in den Circul geometrisch sollen eingeschrieben werden etc. — Samt einer kurzen hierzu nöthingen [sic] Buchstaben-Rechenkunst und Geometrie […], Esslingen, 1741
- (la) Articles dans les Commentarii Societatis Regiæ Scientiarum Gottingensis[19] :
- vol. 1, 1752 :
- « Latitudo geographica Urbis Norimbergæ e novis observationibus deducta » (La latitude de la ville de Nuremberg déduite d'observations nouvelles)
- « Observationes quædam astronomicæ Norimbergæ A. 1749. et 1750 habitæ in ædibus Hommannianis » (Quelques observations astronomiques faites à Nuremberg en 1749 et 1750 chez Homann)
- vol. 2, 1752 :
- « In parallaxin Lunæ eiusdemque a Terra distantiam inquisitio » (Recherche sur la parallaxe de la Lune et sur sa distance de la Terre) — Lu le
- « Nova methodus perficiendi instrumenta geometrica et novum instrumentum goniometricum» (Nouvelle méthode pour réaliser des instruments géométriques et un nouvel instrument goniométrique) – Lu le
- « Novæ tabulæ motuum Solis et Lunæ » (Nouvelles tables des mouvements du Soleil et de la Lune)
- vol. 3, 1753 :
- « Tabularum lunarium usus […] in investiganda longitudine maris » (Usage des tables lunaires dans la recherche de la longitude en mer)
- « Observationes astronomicæ a[nno] 1753 Gottingæ habitæ » (Observations astronomiques faites à Göttingen en 1753)
- vol. 4, 1754 :
- vol. 1, 1752 :
- « Wien », dans Göttingische Anzeigen von den gelehrten Sachen, 1753, p. 1117–1120[20]
- « Versuch einer Erklärung des Erdbebens » (Essai d'explication du tremblement de terre), dans Nützliche Samlungen, 1756, p. 289–296
- Theoria Lunæ juxta systema Newtonianum […] edita jussu præfectorum rei longitudinariæ (Théorie de la Lune selon le système newtonien publiée sur l'ordre des directeurs du bureau [anglais] des longitudes), Londres, Richardson & Clark, 1767[21]
- Tabulæ motuum Solis et Lunæ novæ et correctæ auctore Tobia Mayer : quibus accedit methodus longitudinum promota eodem auctore (Nouvelles tables corrigées des mouvements du Soleil et de la Lune par Tobias Mayer — Méthode [pour déterminer] la longitude proposée par le même), Londres, Richardson, 1770
- Mayer's lunar tables, improved by Mr. Charles Mason. Published by order of the Commissioners of Longitude, 1787
- Astronomical observations made at Göttingen from 1756 to 1761, 1826
- Mathematischer Atlas (Atlas mathématique)[22], 1745 — Écrit avec Johann Wolfgang Baumgarten et Johann Georg Pinitz[23],[24]
- Georg Christoph Lichtenberg (éd.), Tobiae Mayeri […] opera inedita : commentationes Societatis Regiæ Scientiarum oblatas quae integræ supersunt cum tabula selenographica complectens, 1775, p. 394–413 — Lichtenberg a écrit un appendice sur les observations. Contient De affinitate colorum commentatio
- Tobias Mayer's Opera inedita : the first translation of the Lichtenberg edition of 1775, trad. Eric G. Forbes, Macmillan, 1971, 166 p.
- (avec Samuel Vince, James Bradley, Nicolas-Louis de Lacaille et le baron Franz Xaver von Zach) A complete system of astronomy, Londres, G. Woodfall, 3 vol., 1808–14 — En ligne : vol. 1vol. 2 ; vol. 3
- Kosmographische Nachrichten und Sammlungen auf das Jahr 1748, 1850
- Erhard Anthes (dir.), Schriften zur Astronomie, Kartographie, Mathematik und Farbenlehre, Georg Olms (ISBN 3-487-11238-8)
Cartes
- La Comté de Glatz avec le [sic] Principauté de Munsterberg dressée sur des dessins autographes — Comitatus Glaciensis tabula geogr[aphica] ex autographis delineationibus depromta, Héritiers de Homann, 1747
- Carte des Indes Orientales, 1748
- Ducatus Silesiæ tabula geographica generalis statui hodierno — Le Duché de Silésie suivant l'état présent, 1749
- Mondkarte (Carte de la Lune), v. 1750
- Iter Mayerianum ad musas Goettingensis Norimberga, 1751
- [Lan]dgraviatus Hasso-Darmstattini et omnium eo spectantium terrarum repræsentatio geographica, fo 1, 1751
- Carte critique de l'Allemagne — Germaniæ […] Mappa critica
- (avec Jean Palairet (en)) Bowles new pocket map of the Seven United Provinces with their dependencies
Correspondance
- Eric G. Forbes, The Euler–Mayer correspondence, 1751–1755 : a new perspective on eighteenth-century advances in the lunar theory, American Elsevier, 1971, 117 p.
- Eric G. Forbes, « La correspondance astronomique entre Joseph-Nicolas Delisle et Tobias Mayer », dans Revue d'histoire des sciences, vol. 36, no 2, 1983, p. 113–151 — Dix lettres (1748–1751), avec un article de Forbes. Joseph-Nicolas Delisle est un cartographe français.
- Eric G. Forbes et Jacques Gapaillard, « La correspondance astronomique entre l'abbé Nicolas-Louis de Lacaille et Tobias Mayer/The astronomical correspondence between the abbé Nicolas-Louis de Lacaille and Tobias Mayer », dans Revue d'Histoire des Sciences, 49 (4):483-541 (1996) — L'abbé de Lacaille est un astronome français.
Bibliographie
- Erhard Anthes et Armin Hüttermann (dir.), Tobias Mayers Beiträge zur Wissenschaft des 18. Jahrhunderts im Lichte neuerer Untersuchungen, 2013 (ISBN 978-3-944913-39-1)
- Peter Aufgebauer, Die Anfänge der Sternkunde in Göttingen (Les débuts de l’astronomie à Göttingen), dans Göttinger Jahrbuch, t. 50, 2002, p. 75–92.
- Samuel Baur, « Tobias Mayer », dans Gallerie historischer Gemählde aus dem achtzehnten Jahrhundert, vol. 6, 1806, p. 63–68.
- Bernd Feicke, « Mayer (Majer), Tobias », dans Biographisch-Bibliographisches Kirchenlexikon, t. 33, Nordhausen, Bautz, 2012 (ISBN 978-3-88309-690-2), p. 811–815.
- Menso Folkerts, « Mayer, Tobias », dans Neue Deutsche Biographie, t. 16, Berlin, Duncker & Humblot, 1990, p. 528–530 (ISBN 3-428-00197-4).
- Publications d'Eric G[ray] Forbes[25] (liste partielle) :
- « Tobias Mayer's Lunar Tables », dans Ann. Sci. 22 (2):105-116, 1966.
- « The Life and Work of Tobias Mayer (1723-62) », dans Quarterly journal of the Royal Astronomical Society, vol. 8 (1967), p. 227 Bibcode : 1967QJRAS...8..227G
- « Tobias Mayer's theory of colour-mixing and its application to artistic reproductions », dans Ann. Sci. 26 (2):95-114, 1970.
- « A case of forgotten genius », dans British Journal for the History of Science 5 (1):1-20, 1970.
- « Tobias Mayer's method of measuring the areas of irregular polygons », dans Ann. Sci. 26 (4):319-329, 1970.
- « Tobias Mayer's method for calculating the circumstances of a solar eclipse », dans Ann. Sci. 28 (2):177-189, 1970.
- « Tobias Mayer's new astrolabe : its principles and construction », dans Ann. Sci. 27 (2):109-116, 1971.
- « Georg Christoph Lichtenberg and the Opera Inedita of Tobias Mayer », dans Ann. Sci. 28 (1):31-42, 1972.
- The unpublished writings of Tobias Mayer, vol. I : Astronomy and Geography ; vol. II : Artillery and Mechanics ; vol. III : The Theory of the magnet and its application to terrestrial magnetism. (Arbeiten aus der Niedersächsischen Staats- und Universitätsbibliothek Göttingen, vol. 9–11), Göttingen, Vandenhoeck and Ruprecht, 1972[26].
- Tobias Mayer (1723–62). Pioneer of enlightened science in Germany, Göttingen, 1980. (Travaux de la bibliothèque universitaire et de l’état de Basse-Saxe) Göttingen, t. 17.
- « Tobias Mayer's contributions to observational astronomy », dans Journal for the history of astronomy, vol. 11, p. 28, 1980 Bibcode : 1980JHA....11...28F
- Siegmund Günther, « Mayer, Johann Tobias » [sic], dans Allgemeine Deutsche Biographie, t. 21, Duncker & Humblot, Leipzig, 1885, p. 109–116.
- Armin Hüttermann, Tobias Mayer und Nürnberg — Von der Mathematik über die Kartografie zur Astronomie (Des mathématiques à l’astronomie via la cartographie, dans Regiomontanusbote, Zeitschrift der Nürnberger Astronomischen Arbeitsgemeinschaft (Regiomontanusbote, bulletin de la société d’astronomie de Nuremberg), 25e année 3/3012, p. 14–19.
- [Hütterman 2002] Armin Hüttermann, « Tobias Mayer und seine Reisekarte von 1751 », dans Cartographica helvetica, cahier 26, .
- Abraham Gotthelf Kästner, Elogium Tobiae Mayeri, Göttingen, 1762
- Bernhard Jenny et Peter Mesenburg, « MapAnalyst – Analyse und Visualisierung zur Genauigkeit der Mappa critica des Tobias Mayer (1750) », dans Cartographica Helvetica, 43 (2011) p. 43–48
- Peter H. Meurer, Hintergründe und Analysen zu Tobias Mayers « Kritischer Karte von Deutschland » (Contexte et analyse de la Carte critique de l’Allemagne de Tobias Mayer), dans Cartographica Helvetica, cahier 12 (1995) p. 19–26.
- Jean-Étienne Montucla, Histoire des mathématiques, t. 4, 1802, p. 54 et suivantes
- (en) John J. O'Connor et Edmund F. Robertson, « Tobias Mayer », dans MacTutor History of Mathematics archive, université de St Andrews (lire en ligne).
- Erwin Roth et al., Tobias Mayer. Pionier der Positionsbestimmung. Wegbereiter der modernen Navigationssysteme (Tobias Mayer. Pionnier du calcul de la position. Précurseur du système moderne de navigation), Marbach, 1995
- Bernhard Weißbecker, Das Uhrwerk des Mondes : Tobias Mayer und der Längenpreis (ISBN 978-3-8448-3148-1) — Préface et table des matières
- [Wepster 2010] Steven Wepster, Between theory and observation. Tobias Mayer´s explorations of lunar motion 1751-1755, Springer, 2010, Sources and studies in the history of mathematics and the physical sciences, 2009
- Steven Wepster, The method of lunar distances and Tobias Mayer’s lunar tables, 20131. Longitude by lunar distances ; 2. Tobias Mayer and lunar motion research.

Mémoire
- La maison de naissance de Tobias Mayer héberge depuis 1996 le musée Tobias Mayer[27]. Elle se situe non loin de la maison natale de Friedrich Schiller au No 13 de la rue Torgasse à Marbach am Neckar. Le musée a été réalisé et est géré par l’association Tobias Mayer.
- Le cratère lunaire T. Mayer (en) est ainsi nommé par Johann Hieronymus Schröter en 1802.
- Il y a une école Tobias-Mayer à Marbach am Neckar[28].
- Il y a une rue Tobias Mayer à Esslingen am Neckar[29].
Notes et références
- « Tobias » sera cité dans maints ouvrages de façon erronée comme « Johann Tobias ». Selon le livre de baptême et les publications originales, son prénom est simplement Tobias. Par contre Johann Tobias est bel et bien le nom de son fils.
- Baur 1806, p. 63.
- Aujourd’hui le gymnasium Georgii.
- Forbes 1967, p. 230.
- Voir aussi la note 8 de Forbes 1967.
- http://www.tobias-mayer-verein.de/index.php?id=29.
- Le travail lui rapporte deux pièces d'argent : http://www.tobias-mayer-verein.de/index.php?id=29.
- Forbes 1967, p. 233.
- « Tobias Mayer », site Astronomie in Nürnberg.
- Le voyage de noces consiste dans le trajet Nuremberg–Göttingen, où Mayer vient d'être nommé ; le nouvel époux en profite pour dresser la carte de voyage de son itinéraire (Iter Mayerianum ad musas Goettingensis Norimberga) : Hütterman 2002, p. 15. On peut voir la carte sur un site de l'université de Brême. Le dessinateur est Johann Andreas Friedrich Yelin.
- Selon Gauß (lettre à Olbers du 26 octobre 1802), Mayer avait la réputation d'être un mauvais professeur.
- Armin Hüttermann, « Ausstellung in der Paulinerkirche zeigt Werk des Göttinger Gelehrten ». Sur Gauß et Mayer, consulter : Eric G. Forbes, « The astronomical work of Carl Friedrich Gauss (1777–1855) ».
- Roger H. Guichard, Jr., Niebuhr in Egypt, p. 39.
- Forbes 1967, p. 238.
- « Cercles de Borda », page des Amis du Musée scientifique Louis-le-Grand.
- Johann Heinrich von Mädler, Geschichte der Himmelskunde von der ältesten bis auf die neueste, vol. 2, 1873, p. 531. L'amélioration de Borda consista en l'« adjonction d'un deuxième ensemble lunette-alidade, en dessous du cercle azimutal » : page des Amis du Musée scientifique Louis-le-Grand.
- Notre texte est une traduction de : Otto-Joachim Grüsser, « Quantitative visual psychophysics during the period of European enlightenment. The studies of the astronomer and mathematician Tobias Mayer (1723-1762) on visual acuity and colour perception », dans Doc Ophthalmol, fév. 1989 71(2):93-111 (résumé par l'auteur de l'article) . Nous avons mis le texte au présent et l'avons séparé en alinéas. Les notes sont de nous.
- L'article fondateur sur cette question est : Otto-Joachim Grüsser, « The discovery of the psychophysical power law by Tobias Mayer in 1754 and the psychophysical hyperbolic law by Ewald Hering in 1874 », dans Behavioral and Brain Sciences, 16 (1):142, 1993.
- À moins que le contexte ne l'interdise, la « Société royale » sera dans cet article la Société royale des sciences (de Göttingen), qui est aujourd'hui l'Académie des sciences de Göttingen.
- Source : Hütterman 2002, p. 22.
- Date selon la page de titre.
- Titre complet : Mathematischer Atlas, in welchem auf 60 Tabellen alle Theile der Mathematic vorgestellet und nicht allein überhaupt zu bequemer Wiederholung, sondern auch den Anfängern besonders zur Aufmunterung durch deutliche Beschreibung u. Figuren entworfen werden.
- Frank Swetz, « Mayer's Mathematical Atlas ».
- Autre numérisation : Linda Hall Library.
- L'association Tobias-Meyer fait remonter à 1970 la « renaissance de Mayer » et en attribue le mérite à Eric G. Forbes : « Kurzbiographie ». Steven Wepster (Wepster 2010, p. 1) est de cet avis.
- Roderick W. Home, Recension, dans The British Journal for the History of Science, vol. 7, no 3 (nov., 1974), p. 296–298.
- Site officiel.
- Site de l'école.
- Page sur le site de la ville.
Liens externes
- Notices d'autorité :
- Fichier d’autorité international virtuel
- International Standard Name Identifier
- Bibliothèque nationale de France (données)
- Système universitaire de documentation
- Bibliothèque du Congrès
- Gemeinsame Normdatei
- Bibliothèque nationale d’Espagne
- Bibliothèque royale des Pays-Bas
- Bibliothèque nationale de Pologne
- Bibliothèque nationale de Pologne
- Bibliothèque nationale d’Israël
- Bibliothèque universitaire de Pologne
- Bibliothèque apostolique vaticane
- Bibliothèque nationale d’Australie
- Bibliothèque nationale tchèque
- WorldCat
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Ressources relatives à la recherche :
- Ressource relative à l'astronomie :
- (de) « Publications de et sur Tobias Mayer », dans le catalogue en ligne de la Bibliothèque nationale allemande (DNB).
- (de) « Mayer, Tobias », sur deutsche-biographie.de
- (de) Beitrag bei Astronomie in Nürnberg
- (de) Ein historischer Repetitionstheodolit sur www.alpentunnel.de, consulté le
- Narciso Silvestrini et Ernst Peter Fischer (de), colorsystem — Systèmes de couleurs dans l'art et les sciences : Tobias Mayer
- Portail des sciences
- Portail des mathématiques
- Portail de l’astronomie
- Portail du XVIIIe siècle
- Portail du Saint-Empire romain germanique




