Transformation active et passive
En géométrie analytique, les transformations actives et passives font partie des transformations affines utilisées pour placer des objets dans l'espace ou pour effectuer des changements de repère. Elles permettent la transformation spatiale dans l'espace euclidien tridimensionnel d'un vecteur qui si elle le modifie est active et si elle permet un changement de la base est passive[1].
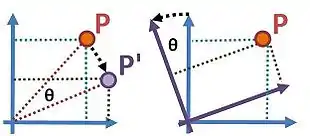
exemple de transformation
Annexes
Notes et références
- (en) Eric W. Weisstein, « Alibi Transformation », sur mathworld.wolfram.com (consulté le )
Articles connexes
- Transformations affines
- Transformations de Lorentz
- Translation
- Vecteur contravariant, covariant et covecteur
- Portail de la géométrie
Cet article est issu de Wikipedia. Le texte est sous licence Creative Commons - Attribution - Partage dans les Mêmes. Des conditions supplémentaires peuvent s'appliquer aux fichiers multimédias.