Transition laminaire-turbulent
La transition laminaire-turbulent est le mécanisme par lequel un écoulement passe de l'état laminaire à l'état turbulent. Sa description utilise généralement le nombre de Reynolds qui mesure localement le rapport entre les forces d'inertie et les forces liées à la viscosité.
Il s'agit d'un phénomène d'instabilité complexe, dépendant de conditions telles que l'état de surface dans le cas d'une couche limite ou les perturbations sonores appliquées.
Ce phénomène, réversible (on parle dans ce cas de relaminarisation), a été étudié essentiellement dans le contexte des couches limites mais s'applique à tout type d'écoulement.
Histoire
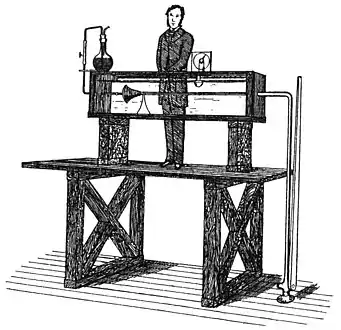 Montage expérimental de Reynolds en 1883.
Montage expérimental de Reynolds en 1883.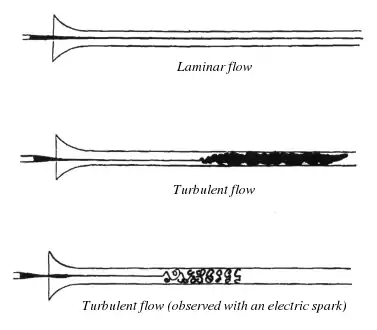 Observations faites par Reynolds dans ses expériences.
Observations faites par Reynolds dans ses expériences.
En 1883 Osborne Reynolds réalise ses premières expériences en conduite en verre avec l'eau[1],[2]. De ses expériences il tire un critère de début de transition en mettant en avant un nombre sans dimension qui sera par la suite nommé nombre de Reynolds par Arnold Sommerfeld[3]. Il montre que dans ses expériences ce paramètre peut varier dans une grande plage de valeurs allant de 2000 pour une paroi d'entrée rugueuse, et jusqu'à 40000 en prenant d'extrêmes précautions sur l'injection d'eau[4].
Les bases mathématiques de la théorie de la stabilité d'un écoulement ont été établies par William McFadden Orr[5],[6] et Arnold Sommerfeld[3] en 1907.
Étapes de la transition en couche limite
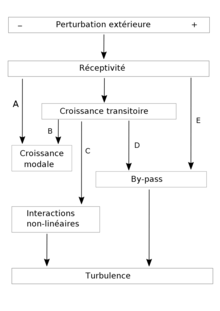
Il existe divers chemins conduisant à la turbulence. Ils ont été particulièrement étudiés pour la couche limite[7]. La première étape est bien sûr de connaître la réceptivité de l'écoulement, c'est-à-dire la façon dont une excitation externe va créer une perturbation dans l'écoulement lui-même[8].
Excitation des modes propres
L'excitation des modes propres qui, s'ils sont instables, conduisent à l'amplification d'ondes jusqu'à une phase non linéaire et la création de spots turbulents (chemin A). Cela peut être des ondes de Tollmien-Schlichting dans le cas le plus simple, de tourbillons de Görtler sur une surface concave ou d'instabilités dans la composante transversale d'un écoulement (crossflow)[9]. Dans ce cas une étude de stabilité peut être faite pour chaque mode pris séparément. En écoulement incompressible cela conduit à l'équation de Orr-Sommerfeld.
Croissance transitoire
L'interaction des divers modes propres, mêmes stables, peut conduire à une croissance transitoire des perturbations si la perturbation est d'amplitude suffisante. Ces perturbations seront amorties ou au contraire conduiront (chemin C) à la phase non linéaire, suivant les conditions locales. Ce scénario, issu du calcul, n'a pas été mis en évidence expérimentalement.
By-pass
On peut observer le passage direct à la turbulence à partir de fortes perturbations (chemin D). C'est le cas de la transition induite par les rugosités de paroi. Dans ce cas la phase non linéaire de croissance est by-passée. Dans le cas de très fortes perturbations la turbulence apparaît directement (chemin E).
Critères de début de transition
Il n'existe pas de critère universel permettant de prévoir la transition. Chaque situation est un cas d'espèce pour lequel l'expérience permet d'établir une corrélation. Le plus souvent celle-ci utilise un nombre de Reynolds basé sur une longueur caractéristique de la couche limite ou de la rugosité. La dispersion de l'écart observé par rapport à la valeur expérimentale peut tout autant être due au défaut de modélisation qu'à la dispersion naturelle du phénomène, celle-ci pouvant être très importante.
Une seule méthode peut prétendre à une certaine universalité : c'est la méthode eN basée sur un calcul des taux d'amplification d'une instabilité linéaire. Cette méthode est lourde à mettre en œuvre et nécessite en tout état de cause l'usage d'un facteur d'ajustement[10].
Intermittence
La transition se caractérise par l'apparition de spots turbulents qui finissent par recouvrir tout l'espace[11]. Ce phénomène est reproductible par un calcul direct de l'écoulement par simulation des grandes structures de la turbulence[12]. Ceci se caractérise en tout point par une intermittence de toutes les quantités locales, phénomène déjà observé par Reynolds.
Ce phénomène se traite en pratique par diverses corrélations. Son étude physique relève de la dynamique des systèmes non linéaires[13],[14].
Relaminarisation
Le retour à un écoulement laminaire peut se produire dans diverses situations : forte accélération de l'écoulement, importante dissipation ou travail de forces extérieures[15]. Ceci a été utilisé dans l'aéronautique pour les tentatives de contrôle de l'écoulement[16].
Quelques cas pratiques de transition laminaire-turbulent

La couche limite qui se développe sur les corps 2D et 3D placés dans un écoulement connaît une transition laminaire-turbulent à un certain nombre de Reynolds. La transition de cette couche limite modifie beaucoup l'écoulement sur ces corps, en cela que la couche limite laminaire résiste beaucoup moins bien aux séparations de couche limite (ou décollements) que la couche limite turbulente. Un cas typique de cette influence de l'état de la couche limite (état laminaire ou état turbulent) est la crise de traînée de la sphère : pour un très faible accroissement du nombre de Reynolds, le coefficient de traînée de la sphère peut être divisé par 5. Le cylindre infini lui-même, lorsqu'il est présenté en travers d'un écoulement, connaît lui aussi une crise de traînée (également liée au changement d'état de la couche limite).
Les crises de traînée de la sphère et du cylindre sont les archétypes des crises de traînée de corps 3D et 2D. Tous les corps suffisamment profilés[17] connaissent une crise de traînée (liée à la transition de leur couche limite). Le graphe ci-contre dessine la crise de traînée de profils symétriques de différentes épaisseurs selon le Reynolds longitudinal de leur écoulement (à incidence nulle)[18],[19] (la crise de traînée du cylindre figure sur ce graphe).
Mise en garde contre la confusion entre l'état (laminaire ou turbulent) de la couche limite et l'état du reste de l'écoulement
Il convient d'attirer l'attention des lecteurs sur une confusion fréquente entre l'état de la couche limite sur un corps et l'état de l'écoulement autour de ce corps : Comme le montre l'exemple des corps profilés (2D ou 3D), ce n'est pas parce que la couche limite qui se développe à leur surface a effectué sa transition de l'état laminaire à l'état turbulent que l'écoulement sur ces corps devient chaotique : au contraire, l'état turbulent de la couche limite conduit souvent à des réattachements (ou recollement) de l'écoulement sur l'aval de ces corps, c.-à-d. que l'écoulement est souvent beaucoup plus laminaire à l'extérieur d'une couche limite turbulente qu'à l'extérieur d'une couche limite laminaire (cette dernière favorisant les décollements de culot, donc un écoulement chaotique sur l'aval des corps). C'est si vrai qu'à l'extérieur de la couche limite sur un corps profilé on peut utiliser le théorème de Bernoulli alors que ce serait une faute de l'utiliser avec un écoulement décollé (et chaotique)[20].
En conséquence, il faut se garder d'utiliser sans précisions des expressions comme écoulement laminaire ou écoulement turbulent alors que la couche limite de ces écoulement est dans un état turbulent ou laminaire... En d'autre termes, l'état laminaire, qui peut apparaître comme souhaitable (parce que doux et régulier), ne convient pas forcément à la couche limite (l'état laminaire de la couche limite conduisant souvent à des décollements de culot sur les corps profilés, donc à une nette augmentation de leur ). C'est pour cela que, dans certains cas, on suscite la transition de la couche limite à l'état turbulent par l'usage de turbulateurs, ceci dans le dessein de diminuer le .
Les propos qui viennent d'être tenus conviennent encore aux cas très particuliers des profils laminaires (2D et 3D) qu'on gagnerait à toujours appeler profil à laminarité étendue de leur couche limite : ce sont des corps dont la forme très particulière recule au maximum la transition de leur couche limite (toujours depuis l'état laminaire jusqu'à l'état turbulent).
Références
- (en) Osborne Reynolds, « An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels », Philosophical Transactions, (lire en ligne)
- (en) Olivier Darrigol, Worlds of Flow. A History of Hydrodynamics from the Berboullis to Prandtl, Oxford University Press, , 356 p. (ISBN 978-0-19-856843-8, lire en ligne)
- (de) A. Sommerfeld, « Ein Beitrag zur hydrodynamische Erklärung der turbulenten Flüssigkeitsbewegungen », Proceedings of the 4th International Congress of Mathematicians, Rome, vol. III, , p. 116-124
- (en) Osborne Reynolds, « On the dynamical theory of incompressible viscous fluids and the determination of the criterion », Philosophical Transactions, (lire en ligne)
- (en) W. Mc F. Orr, « The Stability or Instability of the Steady Motions of a Perfect Liquid and of a Viscous Liquid. Part I: A Perfect Liquid », Proceedings of the Royal Irish Academy. Section A: Mathematical and Physical Sciences, vol. 27, , p. 9-68 (lire en ligne)
- (en) W. Mc F. Orr, « The Stability or Instability of the Steady Motions of a Perfect Liquid and of a Viscous Liquid. Part II: A Viscous Liquid », Proceedings of the Royal Irish Academy. Section A: Mathematical and Physical Sciences, vol. 27, , p. 69-138 (lire en ligne)
- (en) M. V. Morkovin, E. Reshotko et T. Herbert, « Transition in Open Flow Systems. A Reassessment », Bulletin of the American Physical Society, vol. 39, , p. 1882
- (en) William S. Saric, Helen L. Reed et Edward J. Kerschen, « Boundary-Layer Receptivity to Freestream Disturbances », Annual Review of Fluid Mechanics, vol. 34, , p. 291–319
- (en) D. Arnal et G. Casalis, « Laminar-Turbulent Transition Prediction in Three Dimensional Flows », Progress in Aerospace Sciences, vol. 36, no 2, , p. 173-191 (DOI 10.1016/S0376-0421(00)00002-6)
- (en) D. Arnal, Boundary Layer Transition : Predictions Based on Linear Theory, In Progress in Transition Modeling, AGARD Report No 793,
- (en) Maher Lagha, « Turbulent spots and waves in a model for plane Poiseuille flow », Physics of Fluids, vol. 19, , p. 124103 (lire en ligne)
- (en) James Strand et David Goldstein, DNS of Riblets to Control the Growth of Turbulent Spots, 45th AIAA Aerospace Sciences Meeting and Exhibit, (lire en ligne)
- (en) Christophe Letellier, « Intermittency as a transition to turbulence in pipes: Along tradition from Reynolds to the 21st century », Comptes-Rendus Mécanique,
- (en) James J. Riley et Mohamed Gad-el-Hak, The Dynamics of Turbulent Spots, In: Davis S.H., Lumley J.L. (eds) Frontiers in Fluid Mechanics. Springer, (ISBN 978-3-642-46545-1)
- (en) R. Narasimha et K. R. Sreenivasan, « Relaminarization of Fluid Flows », Advances in Applied Mechanics, vol. 19, , p. 221-309 (DOI 10.1016/S0065-2156(08)70311-9)
- (en) Lucio Maestrello, Transition Delay and Relaminarization of Tubulent Flow, ICASE/NASA LaRC Series: Instability and Transition, , 153-161 p. (ISBN 978-1-4612-8008-8, lire en ligne)
- Il n'y a guère que les corps non profilés (comme le disque, la palette infinie présentés frontalement à l'écoulement, etc.) qui ne développent pas de crise de traînée (en conséquence leur est le même à tous les Reynolds).
- S. F. Hoerner, Résistance à l'avancement dans les fluides, Gauthier-Villars éditeurs Paris Gauthier-Villars éditeurs, Paris
- (en) S. F. Hoerner, FLUID-DYNAMIC DRAG
- Se souvenir que le théorème de Bernoulli ne doit jamais être utilisé à l'intérieur d'une couche limite (laminaire ou turbulente).
- Portail de la physique