Treillis de Galois
Un treillis de Galois est un treillis dont la construction est basée sur une correspondance de Galois mais peut aussi être définie en termes de rectangles maximaux d'une relation.
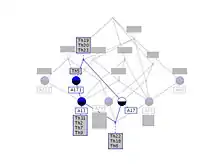
Définition à partir d'une correspondance de Galois
- Soient et deux fonctions définies sur les treillis et telles que soit une correspondance de Galois.
- Soit l'ensemble des couples tels que et
- Soit la relation définie par si et seulement si .
La structure est alors un treillis appelé treillis de Galois.
Définition à partir d'une relation binaire
- Soit une relation binaire.
- On définit un rectangle maximal de comme un couple correspondant à un sous-produit cartésien de maximal pour l'inclusion, c'est-à-dire tel que :
et [1].
- Ces rectangles maximaux , ordonnés par inclusion sur leurs premiers membres - ou dualement sur leurs deuxièmes membres - forment un treillis appelé treillis de Galois.
Cette dualité d'inclusion caractérise les treillis de Galois.
Théorème fondamental des treillis de Galois
Tout treillis peut être le treillis de Galois d'une relation binaire[2]. Réciproquement, deux relations binaires peuvent avoir le même treillis de Galois (ou plus rigoureusement, deux treillis de Galois isomorphes).
Treillis de concepts
Au XVIIe siècle, les jansénistes de Port-Royal ont dans leurs travaux explicité les notions d'intension et d'extension d'un concept, déjà abordées par les philosophes grecs de l'antiquité. On retrouve ces notions philosophiques dans les modes de définitions d'un ensemble mathématique : l'extension d'un ensemble est l'inventaire de ses éléments, tandis que l'intension regroupe les propriétés caractéristiques de cet ensemble.
En 1982, le mathématicien allemand Rudolf Wille (en)[3] a réinvesti ces notions philosophiques dans un cadre algébrique et algorithmique :
- Soit X un ensemble d'objets formels et soit Y un ensemble de propriétés formelles que peuvent avoir ces objets ;
- Soit une relation binaire précisant les propriétés que possèdent ces objets ;
- Alors chaque élément du treillis de Galois correspondant peut être vu comme un concept formel, c'est-à-dire un ensemble d'objets partageant les mêmes propriétés. Le treillis de Galois prend alors le nom de treillis de concepts.
Notes et références
- Cette condition de maximalité peut se traduire par : et .
- Ordre et classification, algèbre et combinatoire. Marc Barbut et Bernard Monjardet, Hachette, 1970.
- Analyse de concepts formels
Voir aussi
Articles connexes
Bibliographie
- Marghoubi, R., Zeitouni, K., & Boulmakoul, A. (2006). Utilisation des treillis de Galois pour l'extraction et la visualisation des règles d'association spatiales. In INFORSID (pp. 703-718).
- Portail des mathématiques