Trou de ver
Un trou de ver (en anglais : wormhole) est, en astrophysique, un objet hypothétique qui relierait deux feuillets distincts ou deux régions distinctes de l'espace-temps et se manifesterait, d'un côté, comme un trou noir et, de l'autre côté, comme un trou blanc[1].
Pour les articles homonymes, voir Trou et Ver (homonymie).
« Pont d'Einstein-Rosen » redirige ici. Pour les autres significations, voir Pont (homonymie).
Ne doit pas être confondu avec un trou noir ni un trou blanc (fontaine blanche) ni le paradoxe d'Einstein-Podolsky-Rosen (EPR).

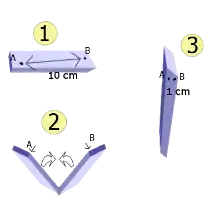
Un trou de ver formerait un raccourci à travers l'espace-temps. Pour le représenter plus simplement, on peut figurer l'espace-temps non en quatre dimensions mais en deux, à la manière d'un tapis ou d'une feuille de papier, dont la surface serait pliée sur elle-même dans un espace à trois dimensions. L'utilisation du raccourci « trou de ver » permettrait un voyage du point A directement au point B en un temps considérablement réduit par rapport au temps qu'il faudrait pour parcourir la distance séparant ces deux points de manière linéaire, à la surface de la feuille. Visuellement, il faut s'imaginer voyager non pas à la surface de la feuille de papier, mais à travers le trou de ver ; la feuille, étant repliée sur elle-même, permet au point A de toucher directement le point B, la rencontre des deux points correspondant au trou de ver.
L'utilisation d'un trou de ver permettrait théoriquement le voyage d'un point de l'espace à un autre (déplacement dans l'espace), le voyage d'un point à l'autre du temps (déplacement dans le temps), et le voyage d'un point de l'espace-temps à un autre (déplacement à travers l'espace et, simultanément, à travers le temps).
Les trous de ver sont des concepts purement théoriques : l'existence et la formation physique de tels objets dans l'Univers n'ont pas été vérifiées. Ils ne doivent pas être confondus avec les trous noirs, dont l'existence a été vérifiée en 2019 et dont le champ gravitationnel est si intense qu’il empêche toute forme de matière de s'en échapper.
Historique
Le physicien autrichien Ludwig Flamm (1885-1964) est parfois présenté comme étant le premier à avoir suggéré, dès 1916[2], l'existence des trous de ver. Mais la communauté scientifique s'accorde[3] pour considérer que leur existence n'a été suggérée qu'en 1935, par Albert Einstein et Nathan Rosen[4].
Les trous de ver (wormholes) doivent leur nom à Charles W. Misner et John A. Wheeler qui désignèrent ainsi en 1957 les propriétés de connexions des différents points de l'espace[5]. Le nom vient de l'analogie de l'asticot et de la pomme, symbole de la gravité depuis Isaac Newton : comme le ver, en rongeant la pomme, peut se rendre directement à un point diamétralement opposé, un vaisseau spatial pourrait utiliser le trou de ver, à la façon d'un raccourci, pour ressortir ailleurs dans l'espace et dans le temps[6].
Quelques années plus tard à l’université Harvard, Stephen Hawking et Richard Coleman reprirent le concept de Wheeler et suggérèrent que l'espace-temps pouvait être soumis à l'effet tunnel précité, reprenant l'idée avancée par Hugh Everett. À l'instar des électrons qui peuvent sauter d'un point à l'autre de l'espace, l'Univers ferait de même. L'effet tunnel créerait des ouvertures dans l'espace-temps qui conduiraient à d'autres univers, des univers cul-de-sac ou tout aussi vastes que le nôtre.
En 2013, Juan Maldacena et Leonard Susskind ont proposé une conjecture qui établit un lien entre l'intrication quantique et le trou de ver[7] : la conjecture ER=EPR[8].
Présentation générale

À l'heure actuelle, différents types de trous de ver ont été décrits de façon théorique :
- le trou de ver de Schwarzschild, infranchissable ;
- le trou de ver de Reissner-Nordstrøm ou de Kerr-Newman, franchissable mais dans un seul sens, pouvant contenir un trou de ver de Schwarzschild ;
- le trou de ver de Lorentz à masse négative, franchissable dans les deux sens.
Tous sont des solutions mathématiques plutôt que des objets concrets.
Ont également été distingués des trous de ver à symétrie sphérique, tels ceux de Schwarzschild et de Reissner-Nordstrøm, qui ne sont pas en rotation, et des trous de ver tels ceux de Kerr-Newmann qui tournent sur eux-mêmes.
Si on essaie de fabriquer un trou de ver à partir de matière à masse positive, il explose et se désintègre. Si une matière à masse négative existe (matière exotique), on peut en principe élaborer un trou de ver statique en accumulant des masses négatives.[réf. souhaitée]
La théorie d'Einstein précise qu'on peut fabriquer n'importe quel type de géométrie spatio-temporelle, statique ou dynamique. Toutefois, une fois la géométrie définie, ce sont les équations d'Einstein qui diront quel devra être le tenseur énergie-impulsion de la matière pour obtenir cette géométrie spatiale. En général, les solutions de trous de ver statiques requièrent une masse négative.
Einstein et Rosen ont sérieusement suggéré que les singularités pouvaient mener à d'autres endroits de l'Univers, d'autres régions de l'espace et du temps. Ces connexions spatio-temporelles sont connues sous le nom de « ponts d'Einstein-Rosen ». Mais ni l'un ni l'autre n'entrevoyaient une possibilité d'entretenir ces connexions en raison du caractère instable des fluctuations quantiques. Selon la formule de John L. Friedman[Qui ?] de l'université de Californie à Santa Barbara, il s'agit d'une « censure topologique »[réf. nécessaire].
Ces trous de vers dits de Lorentz requièrent de la matière exotique pour rester ouverts car celle-ci demande moins d'énergie que le vide quantique, qui subit des fluctuations d'amplitude variables. Il peut s'agir d'énergie négative qui maintiendrait l'ouverture du trou de ver loin de l'horizon. L'ouverture elle-même présente une pression de surface positive [Négative?] qui la maintient ouverte durant les transferts et évite qu'elle ne s'effondre. Seulement, on ne sait comment stocker autant d'antimatière et suffisamment longtemps au même endroit pour entretenir ce tunnel dans l'espace-temps.[réf. nécessaire]

Pour approfondir les conséquences de la relativité générale, Kip Thorne et Richard Morris du Caltech ont tenté de découvrir par le biais de la physique quantique de nouvelles particules capables d'entretenir les trous de ver de Wheeler. Celles-ci ont fait apparaître d'hypothétiques « sas de liaisons » parcourus par des « voyageurs de Langevin ». La littérature de science-fiction s'en est grandement inspirée[9].
Selon John Wheeler, deux singularités pourraient être reliées par un trou de ver, sorte de sas entre deux régions éloignées de l’univers. Entretenir un tel passage et lui donner une taille macroscopique reste un défi théorique. En effet ce « pont » est à l’échelle de Planck : il mesure 10−33 cm et est instable ; il se referme sur lui-même en l’espace de 10−43 s. Si on essaye de l’agrandir, il s'autodétruit. Le trou de ver appartient à la mousse quantique et obéit aux lois probabilistes.
Au contraire d’une singularité, un trou de ver est « nu », il demeure visible et, plus extraordinaire encore, il permet de voyager dans le temps en fonction du sens emprunté.
Exemple : le trou de ver de Morris-Thorne
Le trou de ver de Morris-Thorne (en anglais : Morris-Thorne wormhole)[10] est un trou de ver traversable, décrit par la métrique du même nom.
Ses éponymes sont Michael S. Morris et Kip S. Thorne, qui ont publié leur solution en [11],[12] dans l'American Journal of Physics. Elle consiste en une adaptation du sujet de l'examen final d'un cours d'introduction à la relativité générale, donné au California Institute of Technology en [13].
La métrique de Morris-Thorne s'écrit[14],[15] :
- ,
où :
- sont les coordonnées d'espace-temps :
- est la coordonnée temporelle,
- est la coordonnée radiale,
- est la colatitude,
- est la longitude,
- est une constante,
- est la vitesse de la lumière dans le vide.
En coordonnées de Schwarzschild, elle s'écrit[16] :
- ,
avec .
La « bouche » du trou de ver est une hypersurface ayant la topologie d'une sphère d'aire [17].
La « gorge » du trou de ver est localisée en [17].
Dans la fiction
Le concept des trous de ver est très utilisé dans la science-fiction pour autoriser le voyage dans l'espace, voire dans le temps. Il est souvent utilisé comme prétexte à la découverte de lieux inaccessibles par des moyens conventionnels, et donc à des rencontres avec diverses civilisations ou espèces inconnues. Voici des exemples d'œuvres traitant des trous de vers et de leur utilisation.
Littérature et bande dessinée
Dans la série des romans autour de Honor Harrington se passant dans l'Honorverse créé par David Weber, les trous de ver sont utilisés pour les trajets spatiaux et jouent un rôle important dans l'économie du royaume de Manticore.
Dans Lumière des jours enfuis, publié en 2000, Arthur C. Clarke et Stephen Baxter racontent qu'en 2033, une équipe de chercheurs parvient à transmettre des images par un trou de ver.
Dans la série de bande dessinée de science-fiction Universal War One, l’auteur, Denis Bajram, place la notion de trou de ver au centre de l’intrigue de son œuvre.
Dans la série La Saga du Commonwealth de Peter F. Hamilton, les trous de ver sont devenus, dans le futur, un moyen de transport courant pour se déplacer de planète en planète. Ils sont décrits comme étant très fins, composés d'énergie exotique et modulables en fonction de la quantité d'énergie utilisée pour les créer.
Cette notion est de plus en plus fréquente dans la littérature « Hard science-fiction » : on peut citer Stephen Baxter (Les Vaisseaux du temps, Retour sur Titan, Singularité) ou John Clute (Appleseed), qui offrent une approche romancée de la théorie. Ce concept se retrouve en particulier dans les romans de type néo space opéra. Dans la série de romans The Expanse écrite par Corey James S.A., un trou de ver fabriqué par une ancienne puissance extra-terrestre permet d'accéder à un espace vide entouré de trous de ver ouvrant sur des systèmes planétaires lointains.
Cinéma et séries télévisées
Dans la série Sliders, un tel passage est appelé par erreur « pont Einstein-Rosen-Podolski » au lieu de « ponts d’Einstein-Rosen », par confusion avec le paradoxe Einstein-Podolsky-Rosen, lequel n’a rien à voir avec les trous de ver. Curieusement, le nom est resté chez quelques vulgarisateurs. Podolsky a donc vu son nom associé à un objet particulier de la relativité générale sans avoir travaillé dans ce domaine.
Dans le film Contact est mentionnée une série de vortex appelée « pont d'Einstein-Rosen ».
Toute la série Farscape repose sur la découverte et la compréhension des trous de ver (wormholes en VO, vortex en VF), ceux-ci permettant de parcourir de très grandes distances, de voyager dans le temps et dans d’autres dimensions.
Dans Star Trek: Deep Space Nine, la traduction française utilise vortex pour le terme anglais wormhole, mais il s’agit bien d’un trou de ver utilisé pour voyager de et vers le Quadrant Gamma à 70 000 années-lumière de l'autre côté de la galaxie. La particularité de la station Deep Space Nine est d'être stratégiquement placée à proximité de ce trou de ver, d'où la grande importance de celui-ci dans la série.

Le film de science-fiction Stargate, la porte des étoiles et les séries Stargate SG-1, Stargate Atlantis et Stargate Universe font appel au concept de trou de ver. Un engin appelé porte des étoiles (en anglais stargate) y relie différentes planètes de l’univers en créant un trou de ver de Reissner-Nordstrøm (ou de Kerr-Newman) artificiel. Cependant un corps entier comme celui d'un homme ne survivrait pas au voyage dans le vortex, il est donc démolécularisé par la porte de départ et remolécularisé par la porte d'arrivée. En temps normal, la porte des étoiles ne permet pas de voyager dans le temps, sauf s'il y a un dysfonctionnement (dans un épisode, le vortex passe près d'une éruption solaire et est renvoyé vers la porte de départ mais dans une autre époque). De même, les trous de ver sont utilisés dans les séries Stargate pour faire traverser aux vaisseaux spatiaux de grandes distances en peu de temps en entrant en hyperespace, c'est-à-dire en créant un trou de ver de Reissner-Nordstrøm afin de voyager plus vite que la lumière.
Dans le film Donnie Darko, sorti en 2001, le trou de ver est un élément central permettant un voyage vers le passé.
Dans la série Fringe, l'un des personnages principaux crée un « pont d'Einstein-Rosen » pour voyager dans un univers alternatif. Cet acte sera cause de plusieurs autres trous de vers intempestifs dans les deux univers.
Dans le film Thor, le personnage de Jane Foster parle du Bifröst comme d'un Pont Einstein-Rosen.
Dans l'épisode Le Fantôme de Caliburn de la série Doctor Who, la femme disparue est en fait enfermée dans un univers en perdition, et le seul moyen d'y parvenir est d'utiliser un de ces trous de ver. Ces trous de ver sont aussi cités dans un autre épisode de cette série, L'Invasion des cubes : sept sont éparpillés sur Terre pour mener vers un vaisseau spatial en orbite autour de la planète, alors que des cubes sont envoyés pour arrêter les cœurs humains.
Dans le film Interstellar réalisé par Christopher Nolan et sorti en 2014, un des thèmes principaux est la théorie des trous de ver et son utilisation pour atteindre des planètes potentiellement colonisables situées à des années-lumière de la Terre. Le thème de la distorsion temporelle due à un trou noir y est également important.
Dans le film d'horreur Event Horizon de Paul W.S Anderson sorti en 1997, le système de propulsion du vaisseau est un prototype utilisant une singularité à l'aide d'un trou noir artificiel qui lui permet de créer son propre trou de ver. Ce concept est vulgarisé par le personnage incarné par Sam Neill à l'aide d'un poster érotique emprunté à un des membres de l'équipage.
Dans la série animée Voltron, le défenseur légendaire, les trous de vers sont associés à la magie altéenne[Quoi ?] et ne semblent pas obéir aux lois de la physique.
Dans la série Dark, le destin des protagonistes est influencé par l'existence d'un trou de ver permettant de voyager dans le temps, car le passé, le présent et le futur sont liés formant une boucle temporelle.
Dans la deuxième saison de Star Trek: Discovery, la combinaison temporelle du Dr Burnham permet de voyager dans l'espace-temps au moyen de trous de ver générés par un cristal temporel embarqué.
Dans la saison 6 de the 100 apparaît « l’anomalie » dont on apprend dans la saison 7 qu’il s’agit de trous de ver permettant de se déplacer entre différentes planètes où le temps ne s’écoule pas à la même vitesse (sanctum, Bardo, la terre, etc.) ces trous de ver sont générés par un dispositif appelé la pierre, couverte de symboles et inventée par une civilisation disparue après leur ascension. parfois critiquée, l’influence évidente de stargate marque le scénario de la saison 7 de the 100.
Dans le jeu vidéo Chernobylite, le trou de ver permet au personnage principal de voyager d'un endroit à un autre de la région de Tchernobyl.
Notes et références
- Entrée « trou de ver », dans Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Bruxelles, De Boeck Université, , XI-672 p. (ISBN 978-2-8041-5688-6, BNF 41256105, lire en ligne), p. 507.
- (de) Ludwig Flamm, « Beiträge zur Einsteinschen Gravitationstheorie », Physikalische Zeitschrift, vol. 17, , p. 448-454
- (en) David Lindley, « Focus: The Birth of Wormholes », Physical Review, vol. 15, (DOI 10.1103/PhysRevFocus.15.11)
- (en) Albert Einstein et Nathan Rosen, « The Particle Problem in the General Theory of Relativity », Physical Review, vol. 48, no 1, , p. 73-77 (DOI 10.1103/PhysRev.48.73, Bibcode 1935PhRv...48...73E, lire en ligne, consulté le )
- (en) Charles W. Misner et John A. Wheeler, « Classical physics as geometry », Annals of Physics, vol. 2, no 6, , p. 525-603 (DOI 10.1016/0003-4916(57)90049-0).
- Jean-Pierre Luminet, « Trou noir : la porte des étoiles ? », sur France Inter.fr, (consulté le ).
- (en) Juan Martín Maldacena et Leonard Susskind, « Cool horizons for entangled black holes », Fortschritte der Physik (de), vol. 61, no 9, , p. 781-811 (DOI 10.1002/prop.201300020, Bibcode 2013ForPh..61..781M, arXiv 1306.0533, lire en ligne [PDF], consulté le ).
- (en) Hrant Gharibyan et Robert F. Penna, « Are entangled particles connected by wormholes? Support for the ER=EPR conjecture from entropy inequalities », Physical Review D, vol. 89, no 6, , p. 066001 (DOI 10.1103/PhysRevD.89.066001, Bibcode 2014PhRvD..89f6001G, arXiv 1308.0289, lire en ligne [PDF], consulté le ).
- « Voyage au centre d'un trou de ver », sur Astrosurf (consulté le ).
- Müller 2008, résumé, p. 1.
- Müller 2008, I, p. 1, col. 1.
- Morris et Thorne 1988.
- Morris et Thorne 1988, I, C, p. 398, col. 1.
- Müller 2008, II, p. 2, col. 1 (1).
- Morris et Thorne 1988, p. 398 (B2a).
- Müller 2008, II, p. 2, col. 1 (2).
- Müller 2008, II, p. 2, col. 1.
Annexes
Bibliographie
- (en) Andrew DeBenedictis et A. Das, « On a General Class of Wormhole Geometries », Classical and Quantum Gravity, vol. 18, no 7, , p. 1187-1204 (DOI 10.1088/0264-9381/18/7/304, Bibcode 2001CQGra..18.1187D, arXiv 0009072).
- Stephen Hawking, Une brève histoire du temps. Du Big Bang aux trous noirs, Flammarion, 2005.
- Stephen Hawking et Roger Penrose, La nature de l'espace et du temps, Gallimard, 2003.
- Stephen Hawking, Trous noirs et bébés univers et autres essais, Odile Jacob, 2000.
- Kip S. Thorne, Trous noirs et distorsions du temps : l'héritage sulfureux d'Einstein, trad. Alain Bouquet et Jean Kaplan, Flammarion, 2009. Avec une préface de Stephen Hawking. (ISBN 978-2081224964)
- M. Begelmen et M. Rees, Gravity’s Fatal Attraction : Black Holes in the Universe, W.H.Freeman, 1996.
- (en) Stuart L. Shapiro et Saul A. Teukolsky, « Formation of naked singularities: The violation of cosmic censorship », Physical Review Letters, vol. 66, no 8, , p. 994–997 (DOI 10.1103/PhysRevLett.66.994, lire en ligne, consulté le ).
- (en) Stuart L. Shapiro et Saul A. Teukolsky, « Building Black Holes: Supercomputer Cinema », Science, vol. 241, no 4864, , p. 421–425 (ISSN 0036-8075 et 1095-9203, PMID 17792605, DOI 10.1126/science.241.4864.421, lire en ligne, consulté le ).
- (en) Michael S. Morris, Kip Thorne et Ulvi Yurtsever, « Wormholes, Time Machines, and the Weak Energy Condition », Physical Review Letters, vol. 61, no 13, , p. 1446-1449 (DOI 10.1103/PhysRevLett.61.1446, Bibcode 1988PhRvL..61.1446M, lire en ligne [PDF], consulté le )
- H. Everett III, Reviews of Modern Physics, 29, 1958, p. 454[réf. incomplète].
- Mika - "Akimmik" 1992 - p. 415-712[réf. incomplète].
- (en) Thomas A. Roman, « Some thoughts on energy conditions and wormholes », The Tenth Marcel Grossmann Meeting, (DOI 10.1142/9789812704030_0236, Bibcode 2006tmgm.meet.1909R, arXiv gr-qc/0409090, lire en ligne [PDF], consulté le )
- (en) Edward Teo, « Rotating traversable wormholes », Physical Review D, vol. 58, no 2, (DOI 10.1103/PhysRevD.58.024014, Bibcode 1998PhRvD..58b4014T, arXiv gr-qc/9803098, lire en ligne [PDF], consulté le )
- (en) Matt Visser, « Traversable wormholes: Some simple examples », Physical Review D, vol. 39, no 10, , p. 3182-3184 (DOI 10.1103/PhysRevD.39.3182, Bibcode 1989PhRvD..39.3182V, arXiv 0809.0907, lire en ligne [PDF], consulté le )
- (en) Léo-Paul Euvé et Germain Rousseaux, « Classical analogue of an interstellar travel through a hydrodynamic wormhole », Physical Review D, vol. 96, no 6, (DOI 10.1103/PhysRevD.96.064042)
- [Taillet, Villain et Febvre 2013] R. Taillet, L. Villain et P. Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Sup., hors coll., (réimpr. 2015), 3e éd. (1re éd. ), X-899 p., ill. et fig., 17 × 24 cm (ISBN 978-2-8041-7554-2, EAN 9782804175542, OCLC 842156166, BNF 43541671, SUDOC 167932349, présentation en ligne, lire en ligne), s.v.trou de ver, p. 701, col. 1.
- Sur le trou de ver de Morris-Thorne
- [Ellis 1973] (en) H. G. Ellis, « Ether flow through a drainhole : a particle model in general relativity », J. Math. Phys., vol. 14, no 1, , p. 104-118, article no 16 (OCLC 5542485827, DOI 10.1063/1.1666161, Bibcode 1973JMP....14..104E, résumé, lire en ligne).
- [Bronnikov 1973] (en) K. A. Bronnikov, « Scalar-tensor theory and scalar charge », Acta Phys. Pol. B (en), vol. 4, nos 3-4, , p. 251-266, article no 10 (OCLC 4434848908, lire en ligne).
- [Morris et Thorne 1988] (en) M. S. Morris et K. S Thorne, « Wormholes in spacetime and their use for interstellar travel : A tool for teaching general relativity » [« Les trous de ver dans l'espace-temps et leur utilisation pour les voyages interstellaires : un outil d'enseignement de la relativité générale »], American Journal of Physics, vol. 56, no 5, , p. 395-412, article no 1 (OCLC 4660684580, DOI 10.1119/1.15620, Bibcode 1988AmJPh..56..395M, résumé, lire en ligne [PDF]).
- [Müller 2008] (en) Th. Müller, « Exact geometric optics in a Morris-Thorne wormhole spacetime », Physical Review D, vol. 77, no 4, , p. 2e part. (OCLC 4631578262, DOI 10.1103/PhysRevD.77.044043, Bibcode 2008PhRvD..77d4043M, résumé, lire en ligne [PDF]).
- [James, Tunzelmann, Franklin et Thorne 2015] (en) O. James, E. v. Tunzelmann, P. Franklin et K. S Thorne, « Visualizing Interstellar's wormhole » [« Visualiser le trou de ver d'Interstellar »], American Journal of Physics, vol. 83, no 6, , article no 1 pages= (OCLC 5856563581, DOI 10.1119/1.4916949, Bibcode 2015AmJPh..83..486J, arXiv 1502.03809, résumé, lire en ligne [PDF]).
- [Deza et Deza 2014] (en) M. M. Deza et E. Deza, Encyclopedia of distances [« Encyclopédie des distances »], Heidelberg, Springer, , 3e éd. (1re éd. ), XX-733 p., ill. et portr., 25 cm (ISBN 978-3-662-44341-5, EAN 9783662443415, OCLC 898123993, DOI 10.1007/978-3-662-44342-2, SUDOC 182433501, présentation en ligne, lire en ligne), VIe part., chap. 26, § 26.2, s.v.Morris–Thorne metric [« Métrique de Morris-Thorne »], p. 580.
Articles connexes
Liens externes
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Ressource relative à la littérature :
- (fr) Un lien possible entre les trous de ver et l'intrication quantique a été découvert en 2013.
- (en) White holes and Wormholes, Andrew Hamilton, Université du Colorado
- (en) Des méta matériaux permettent d'émuler un trou de ver, selon la théorie d'alcubierre jusqu'à 25 % de la vitesse de la lumière
- Portail de la cosmologie
- Portail de la physique
- Portail de l’astronomie
- Portail de la science-fiction