Méthode des vitesses radiales
La méthode des vitesses radiales, également appelée spectroscopie Doppler, vélocimétrie Doppler ou encore spectrovélocimétrie, est une méthode spectroscopique utilisée pour mesurer la vitesse relative d'objets, le long de l'axe de visée. Elle complète les mesures astrométriques (dans le plan du ciel) en donnant la troisième composante de la vitesse.
Aujourd'hui, cette technique est notamment utilisée dans la recherche d'exoplanètes, où la précision de cette technique est poussée à l'extrême : la précision aujourd'hui atteinte est de l'ordre du mètre par seconde, voire moins, pour des instruments tels que HARPS. Elle implique l'observation de l'effet Doppler-Fizeau dans le spectre de l'étoile autour de laquelle une planète orbite.
Il est extrêmement difficile d'observer une planète extra solaire directement. Le rayonnement indirect de la planète est très faible, comparé au rayonnement direct de son étoile, avec les distances interstellaires, nos télescopes sont éblouis par le rayonnement de l'étoile. De plus ces exoplanètes sont souvent trop petites et trop proches de leur étoile pour pouvoir être observées directement. D'ailleurs, les premières observations directes remontent seulement à 2004 et 2005. En conséquence, la majorité des exoplanètes sont détectées en utilisant des méthodes indirectes, telle la spectroscopie Doppler. Presque toutes les planètes extra solaires connues à ce jour ont été découvertes ou confirmées grâce à cette méthode.
Historique
Isaac Newton étudia la décomposition de la lumière à travers un prisme en 1666-1672. Cette étude a depuis servi dans de nombreux domaines, et notamment en astronomie, où la spectroscopie Doppler est utilisée au moins depuis 1867, lorsque William Huggins et sa femme Margaret utilisèrent cette technique pour mesurer le mouvements de plusieurs objets par rapport à la Terre. Bien que les premières observations ne donnèrent pas de résultats étant donnée la précision limitée des instruments (Huggins l'estime à 16 km/s si l'objet s'éloigne, 32–40 km/s si l'objet s'approche), cette technique finit par porter ses fruits et permit la découverte de nombreux compagnons stellaires puis, bien plus tard, substellaires.
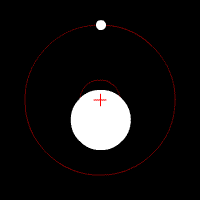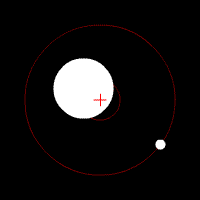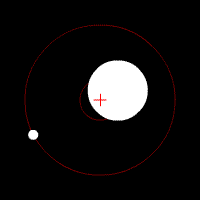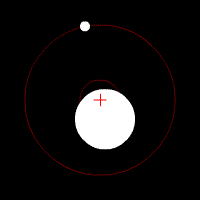
En 1952, Otto Struve propose d'utiliser de puissants spectromètres pour détecter des planètes lointaines. Il décrit comment une planète géante, telle que Jupiter, pourrait provoquer de légères oscillations auprès de son étoile, comme deux objets célestes gravitant autour d'un barycentre commun[1]. Il prédit que la lumière émise par l'étoile subirait de petits changements dus à l'effet Doppler, eux-mêmes causés par des variations périodiques de la vitesse radiale de l'étoile. Ces variations seraient détectables par un spectromètre très sensible, et se traduiraient comme une alternance de redshifts et de blueshifts très légers sur la lumière de l'étoile. Cependant, les instruments de l'époque ne peuvent mesurer la vitesse radiale d'un objet qu'avec une marge d'erreur de 1000 m/s ou plus, ce qui les rendaient inutiles dans la détection de nouvelles planètes[2]. Les changements de vitesse radiale attendus sont en effet très petits — Jupiter cause au Soleil un changement de 13 m/s sur une période de 12 ans, et la Terre un changement de 0,09 m/s sur une période de 1 an — ce qui implique des observations à long terme avec des instruments de très haute résolution[2].
Les progrès des technologies de spectrométrie et d'observation effectués durant les années 80 et 90 ont abouti à des instruments capables de telles recherches. La première exoplanète découverte, orbitant autour d'une étoile semblable au Soleil, 51 Pegasi b, fut détectée en octobre 1995 en utilisant la spectroscopie Doppler[3]. Depuis, plus de 200 planètes extrasolaires ont été identifiées, et la plupart grâce à des programmes de recherches basés au Keck, au Lick et à d'autres observatoires Anglo-Australiens, ainsi que des équipes basées au Geneva Extrasolar Planet Search, en utilisant la méthode des vitesses radiales[3].
Méthode
Une série d'observations sont effectuées sur le spectre de la lumière émise par l'étoile. Des variations dans ce spectre peuvent être détectées, lorsque la longueur d'onde de certaines raies d'absorption spectrales augmente et diminue de façon régulière sur un intervalle de temps donné. Ces variations peuvent être révélatrices de changements dans la vitesse radiale, celle-ci pouvant être altérée par la présence d'une planète en orbite autour de l'étoile, causant l'effet Doppler-Fizeau sur la lumière émise par l'étoile.
Si une planète extrasolaire est détectée, sa masse peut être déterminée à partir des changements de vitesse radiale de son étoile. Un graphique de la vitesse radiale, mesurée par rapport au temps donnera une courbe caractéristique (courbe sinusoïdale dans le cas d'une orbite circulaire), et l'amplitude de la courbe permettra de calculer la masse de la planète.
Techniques d'étalonnage du spectromètre
Étalonnage simultané
Avec cette technique, deux fibres (A et B) recueillent simultanément la lumière de deux sources, lesquelles constituent deux spectres. Une des fibres (A) recueille la lumière de l'étoile alors que l'autre (B) recueille la lumière d'une source d'étalonnage. Les deux spectres obtenus sont comparés à ceux obtenus lors de l'étalonnage, étape pendant laquelle les deux fibres recueillent la lumière d'une source de calibration. L'hypothèse est que la dérive est la même pour les deux fibres. La fibre B ayant recueilli la lumière de la même source aussi bien lors de l'étalonnage que lors de l'observation de l'étoile, la comparaison des deux donne directement la dérive du spectrographe entre les deux poses. En corrigeant le spectre de l'étoile de cette dérive, on peut alors le comparer au spectre d'étalonnage de la fibre A pour mesurer la vitesse de l'étoile.
Les sources d'étalonnage utilisées dans cette technique sont soit des lampes à cathode creuse (thorium-argon par exemple), des interféromètres de Fabry-Perot ou des peignes de fréquence laser.
« Auto-étalonnage » : les cellules à gaz
Avec cette technique, on fait passer la lumière de l'étoile observée à travers une cellule de gaz (fluorure d'hydrogène, iode, …), ce qui fait qu'on ajoute aux raies d'absorption de l'étoile les raies d'absorption du gaz traversé. On peut dès lors obtenir directement la vitesse de l'étoile en comparant la position de ses raies à celle des raies de la cellule de gaz. L'inconvénient de cette technique est la zone couverte par la cellule et le mélange des raies de l'étoile avec celles de la cellule de gaz.
Exemple
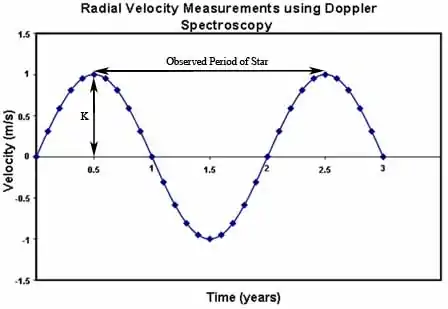
Le graphique à droite illustre la courbe sinusoïdale créée en utilisant la spectroscopie Doppler pour observer une étoile imaginaire autour de laquelle graviterait une planète sur une orbite circulaire. Des observations sur une étoile réelle engendrerait un graphe similaire, bien que l'excentricité orbitale déformerait la courbe et compliquerait les calculs ci-dessous, et que le bruit de mesure rendrait la courbe moins "lisse".
La vitesse de l'étoile théorique montre une variation périodique de 1 mètre par seconde de demi-amplitude, suggérant une masse qui est en orbite autour d'elle. En utilisant la troisième loi de Kepler, la période observée de l'orbite de la planète autour de l'étoile (correspondant à la période à laquelle le spectre de l'étoile se modifie) peut être utilisée afin de déterminer la distance séparant la planète de l'étoile. Ceci peut se faire grâce à l'équation suivante :
où
- est la distance séparant la planète de l'étoile,
- est la constante gravitationnelle,
- est la masse de l'étoile,
- est la période citée plus haut.
Ayant à présent déterminé , la vitesse de la planète autour de l'étoile peut être calculée en utilisant la loi de Newton sur la gravitation :
où est la vitesse de la planète.
La masse de la planète peut alors être calculée à partir de sa vitesse :
où est la vitesse observée de l'étoile principale. La vitesse Doppler observée, , où i est l'inclinaison de l'orbite de la planète par rapport au plan du ciel.
Ainsi, en supposant qu'on ait une valeur pour l'inclinaison de la planète et pour la masse de l'étoile, les changements dans la vitesse radiale de l'étoile peuvent être utilisés pour calculer la masse d'une exoplanète.
Évolution de la précision
| Date | Précision | Instrument (télescope) | Commentaire |
|---|---|---|---|
| 1867 | 16–40 km/s | ||
| 1938 | 0,5 km/s | Meilleure précision atteinte[4] | |
| 1953 | ~750 m/s | ||
| 1977 | 300 m/s | CORAVEL (Suisse de 1 m à l'OHP)[5] | Pour une étoile G, mV=7, 3 min de pose[6]. 500 m/s pour B=13[5]. |
| 1981 | 200 m/s | CORAVEL (Danois de 1,54 m à La Silla) | Pour une étoile G, mV=7, 3 min de pose[6]. Précision de 100 m/s pour mV=7 et 10 min de pose[6]. |
| 1993 | 7 m/s | ÉLODIE (1,93 m de l'OHP) | |
| 1998 | 7 → 2 m/s | CORALIE (Euler 1,2 m) | |
| 2003 | 1 m/s | HARPS (3,6 m de l'ESO) | |
| 2006 | 5-6 m/s | SOPHIE (1,93 m de l'OHP) | |
| ? | 2 m/s | SOPHIE+ (1,93 m de l'OHP) | |
| (2017) | 0,1 m/s | ESPRESSO (VLT) | |
| (20??) | 0,02 m/s | HIRES (E-ELT) |
Problèmes
Le problème majeur inhérent à la méthode est qu'il mesure uniquement le mouvement de l'étoile sur la ligne de visée, et dépend donc de l'inclinaison de l'orbite de la planète ; dans le cas où celle-ci est inconnue, il n'est pas possible de déterminer exactement la masse de la planète par cette méthode. Si le plan orbital de la planète est bel et bien aligné avec la ligne de mire de l'observateur, les variations de la vitesse radiale mesurées correspondent alors à la vraie valeur. Dans le cas contraire, lorsque le plan orbital et la ligne de mire ne sont pas alignés, l'effet que la planète a sur l'étoile sera en réalité plus grand que ce qui a été mesuré à travers les changements de vitesse radiale de l'étoile. Par conséquent, la vraie masse de la planète sera plus grande que prévu.
Afin de corriger cet inconvénient, et déterminer par la même occasion la vraie masse de l'exoplanète, les mesures de vitesse radiale doivent être combinées avec des mesures astrométriques. Celles-ci suivront le mouvement propre de l'étoile dans le plan du ciel, qui est perpendiculaire à la ligne de visée. Ces mesures astrométriques permettent aux chercheurs de vérifier si des objets qui semblent être des planètes de masse élevée ne sont pas plutôt des naines brunes[2].
Un autre problème est que l'enveloppe de gaz peut se dilater et se contracter (de manière périodique dans certains cas), et certaines étoiles sont variables. La spectroscopie Doppler ne convient pas pour trouver des planètes autour de ce type d'étoile, parce que de tels changements dans le spectre de l'étoile peuvent masquer le petit effet causé par la planète.
Cette méthode est la meilleure pour détecter des objets très massifs orbitant près de leur étoile, appelés Jupiters chauds, qui ont un fort effet gravitationnel sur l'étoile et causent donc de grands changements dans sa vitesse radiale. L'observation de nombreuses raies spectrales et de nombreuses périodes orbitales permet d'augmenter le rapport signal sur bruit des observations, ce qui amplifie les changements causés par une planète plus petite ou plus lointaine ; mais la détection de planètes telluriques similaires à la Terre reste impossible avec les instruments actuels.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Doppler spectroscopy » (voir la liste des auteurs).
- (en) Otto Struve, « Proposal for a project of high-precision stellar radial velocity work » The Observatory 72 (1952), pages 199-200.
- (en) David Darling, « Radial velocity method » The Encyclopedia of Astrobiology, Astronomy, and Space Flight, 27 avril 2007.
- (en)R. P. Butler, et al. « Catalog of Nearby Exoplanets »[PDF] The Astrophysical Journal, Vol. 646 (2006) : pages 2-3, 25-33.
- David Belorizky, « Le Soleil, étoile variable », L'Astronomie, vol. 52, , p. 359-361 (lire en ligne)
- « CORAVEL », sur www.obs-hp.fr
- F. Sánchez et M. Vazquez, « New Windows to the Universe: XIth European Meeting of the International Astronomical Union », sur Google Books, Cambridge University Press,
Bibliographie
- James Lequeux, Thérèse Encrenaz et Fabienne Casoli, La révolution des exoplanètes, Les Ulis, EDP Sciences, , 214 p. (ISBN 978-2-7598-2111-2)
- [Lovis et Fischer 2010] (en) Christophe Lovis et Debra A. Fischer, « Radial Velocity », Exoplanets, Tucson (Arizona) : University of Arizona Press, Sara Seager, décembre 2010, 526 pages, p. 27-53 (ISBN 978-0-8165-2945-2, Bibcode 2010exop.book...27L, lire en ligne)