partially ordered set
English
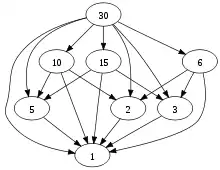
A partially ordered set with the relation "is divisible by"
Noun
partially ordered set (plural partially ordered sets)
- (set theory, order theory, loosely) A set that has a given, elsewhere specified partial order.
- (set theory, order theory, formally) The ordered pair comprising a set and its partial order.
- 1959 [D. Van Nostrand], Edward James McShane, Truman Arthur Botts, Real Analysis, 2005, Dover, page 28,
- A partially ordered set means a pair consisting of a set and a partial order in . As usual, when the meaning is clear, we may suppress the notation of " " and speak of the partially ordered set .
- The ordered fields defined earlier are easily seen to be examples of partially ordered sets.
- 1994, I. V. Evstigneev, P. E. Greenwood, Markov Fields over Countable Partially Ordered Sets: Extrema and Splitting, American Mathematical Society, page 35,
- In sections 7-10 we shall consider random fields over some subsets T of the partially ordered set TM.
- 2000, David Arnold, Abelian Groups and Representations of Finite Partially Ordered Sets, Springer, page 45,
- The invention of a derivative of a finite partially ordered set by Nazarova and Roiter in the late 1960s or early 1970s was a seminal event in the subject of representations of finite partially ordered sets (see [Simson 92]).
- 1959 [D. Van Nostrand], Edward James McShane, Truman Arthur Botts, Real Analysis, 2005, Dover, page 28,
Usage notes
- The two senses are commonly used interchangeably, there rarely being a need to distinguish between them.
- The components of the ordered pair may be referred to separately as the ground set and partial order.
Synonyms
- (set on which a partial order is defined): ground set, poset
- (ordered pair of set and partial order): poset
- See also Thesaurus:partially ordered set
Hypernyms
- (order theory): category
Hyponyms
- (order theory): lattice, totally ordered set
Translations
set having a specified partial order
|
|
See also
- complete partial order
- partial order
Further reading




This article is issued from Wiktionary. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.