Rational Functions
A rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials, nor the values taken by the function, are necessarily rational numbers.
Any function of one variable,
where
Note that every polynomial function is a rational function with
A constant function such as
The Domain of a Rational Function
The domain of a rational function
For a simple example, consider the rational function
Domain restrictions can be calculated by finding singularities, which are the
Factorizing the numerator and denominator of rational
function helps to identify singularities of algebraic rational functions.
Singularity occurs when the denominator of a rational function equals
Example 1
Consider the rational function
The domain of this function includes all values of
We can factor the denominator to find the singularities of the function:
Setting each linear factor equal to zero, we have
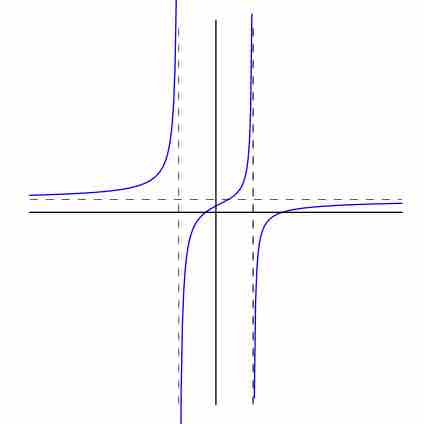
The domain of a function
Graph of a rational function with equation
Note that there are vertical asymptotes at
Example 2
Consider the rational function
The domain of this function is all values of