Chapter 3
Systems of Equations
By Boundless
A system of equations consists of two or more equations with two or more variables, where any solution must satisfy all of the equations in the system at the same time.
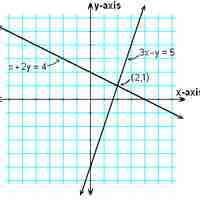
A simple way to solve a system of equations is to look for the intersecting point or points of the equations. This is the graphical method.
The substitution method is a way of solving a system of equations by expressing the equations in terms of only one variable.
The elimination method is used to eliminate a variable in order to more simply solve for the remaining variable(s) in a system of equations.
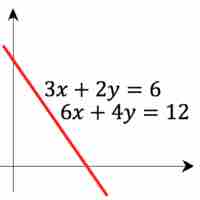
For linear equations in two variables, inconsistent systems have no solution, while dependent systems have infinitely many solutions.
Systems of equations can be used to solve many real-life problems in which multiple constraints are used on the same variables.
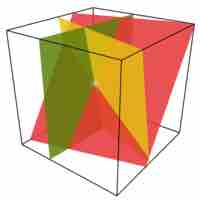
A system of equations in three variables involves two or more equations, each of which contains between one and three variables.
Systems of equations in three variables are either independent, dependent, or inconsistent; each case can be established algebraically and represented graphically.
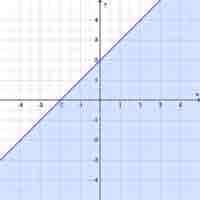
Graphing linear inequalities involves graphing the original line, and then shading in the area connected to the inequality.
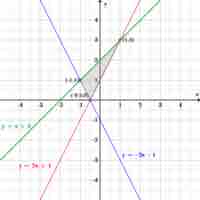
Solving for a system of linear inequalities requires finding values for each of the variables such that all equations are satisfied.
Linear programming involves finding an optimal solution for a linear equation, given a number of constraints.