Section 4
Multiple Integrals
By Boundless

For a rectangular region

An iterated integral is the result of applying integrals to a function of more than one variable.
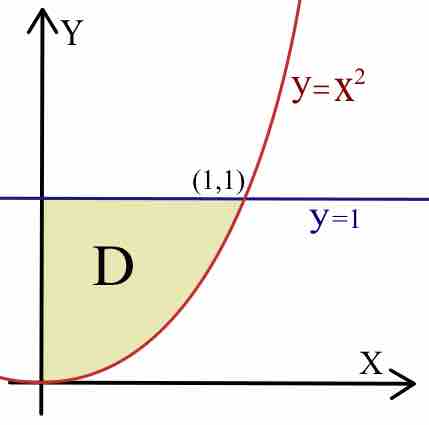
Double integrals can be evaluated over the integral domain of any general shape.
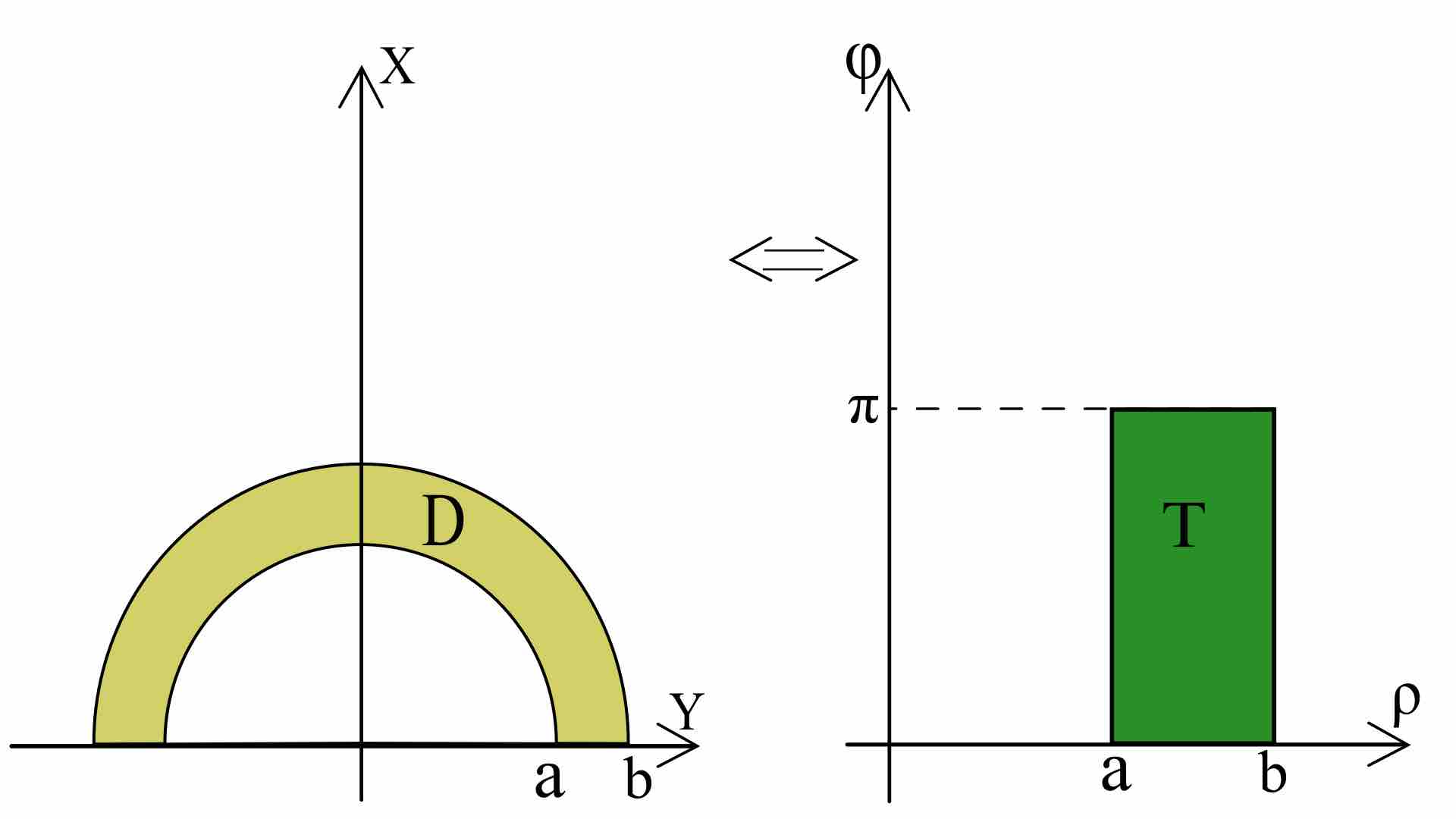
When domain has a cylindrical symmetry and the function has several specific characteristics, apply the transformation to polar coordinates.

When the function to be integrated has a cylindrical symmetry, it is sensible to integrate using cylindrical coordinates.
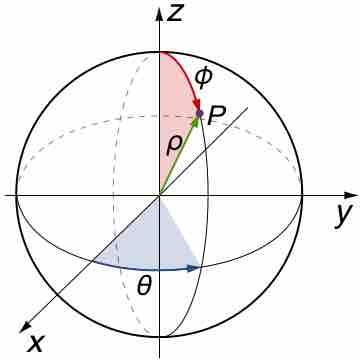
When the function to be integrated has a spherical symmetry, change the variables into spherical coordinates and then perform integration.
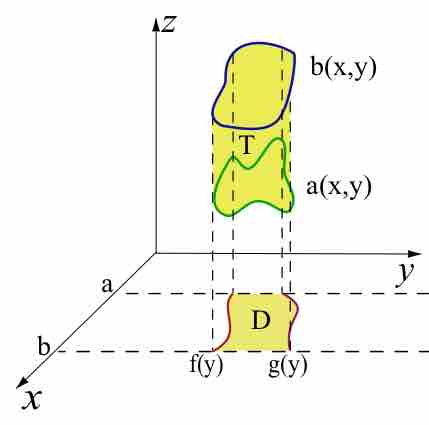
For
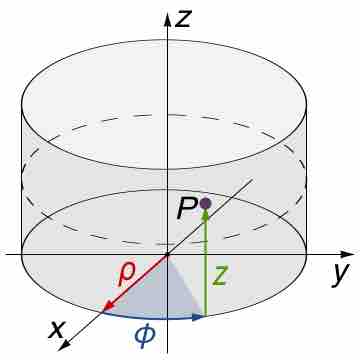
One makes a change of variables to rewrite the integral in a more "comfortable" region, which can be described in simpler formulae.
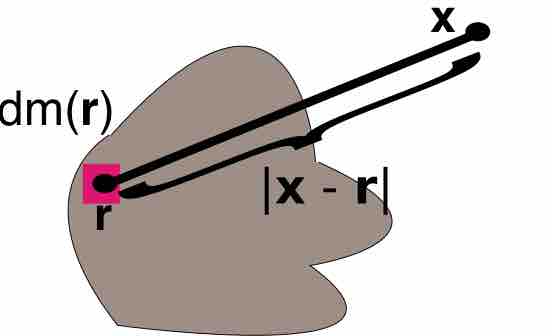
Multiple integrals are used in many applications in physics and engineering.
The center of mass for a rigid body can be expressed as a triple integral.