The Black-Scholes formula is a way of pricing a European option (an option that can only be exercised at its expiration date). The model was originally presented in a 1973 paper by Fischer Black and Myron Scholes who eventually received a Nobel Prize for their work in 1997. The key idea behind the model is to hedge the option by buying and selling the underlying asset in just the right way, and consequently "eliminate risk". This hedge is called delta hedging and is the basis of more complicated hedging strategies such as those engaged in by investment banks and hedge funds. The hedge implies that there is a unique price for the option and this is given by the Black–Scholes formula.
The Black-Scholes formula explains the relationship between the price of the stock, volatility, the price of the financial derivative (such as an option), and time .
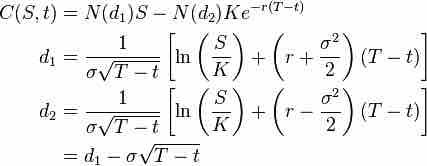
Black-Scholes Model
The Black-Scholes formula where S is the stock price, C is the price of a European call option, K is the strike price of the option, r is the annualized risk-free interest rate, sigma is the volatility of the stock's returns, and t is time in years (now=0, expiry=T).
lt is widely used, although often with adjustments and corrections, by options market participants . Empirically, the Black-Scholes formula is relatively accurate, though there are some discrepancies. The Black-Scholes formula, despite not being 100% accurate, is used because it is:
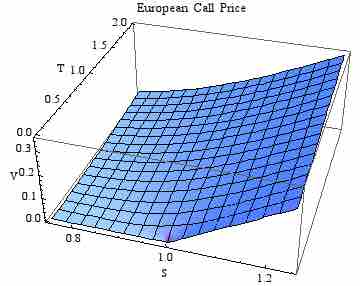
European Call Prices
An example of prices of a European call option over time as predicted by the Black-Scholes formula.
- easy to calculate
- a useful approximation, particularly when analyzing the direction in which prices move when crossing critical points
- a robust basis for more refined models
- reversible, as the model's original output, price, can be used as an input and one of the other variables solved for; the implied volatility calculated in this way is often used to quote option prices
The Black-Scholes formula applies only to equity derivatives, however. This is mainly due to the fact that as a bond reaches maturity, the true value becomes know (the bond issuer has publicly declared how much the bond will be worth at maturity). Since this characteristic is true for bonds but not for equity options, the Black-Scholes model cannot be used for bond valuation.