The definition of a circle is as simple as the shape. A circle is the set of all points that are at a certain distance from a center point. This definition is what gives us the concept of the radius of a circle, which is equal to that certain distance.

Since we know a circle is the set of points a fixed distance from a center point, let's look at how we can construct a circle in a Cartesian coordinate plane with variables $x$ and $y$. To find a formula for this, suppose that the center is the point $\left(a,b\right)$. According to the distance formula, the distance $c$ from the point $\left(a,b\right)$ to any other point $\left(x,y\right)$ is:

 $\displaystyle{c = \sqrt{ \left(x-a\right)^2 + \left(y-b\right)^2}} $

If we now square this equation on both sides, we have:

$\displaystyle{c^{2} = \left(x-a\right)^{2}+\left(y-b\right)^{2}}$

Remember that the distance between the center $\left(a,b\right)$ and any point $\left(x,y\right)$ on the circle is that fixed distance, which is called the radius. So let's change this equation so that it uses $r$ instead of $c$. 

$\displaystyle{r^{2} = \left(x-a\right)^{2}+\left(y-b\right)^{2}}$

This is the general formula for a circle with center $\left(a,b\right)$ and radius $r$. Notice that all we have done is slightly rearrange the distance formula equation.

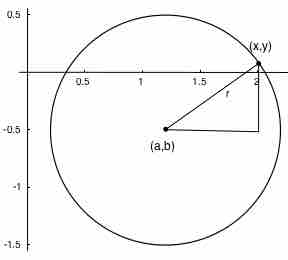
Graph of a circle

The circle with center $\left(a,b\right)$ is graphed in the Cartesian plane.

Parts of a Circle

Now that we have an algebraic foundation for the circle, let's connect it to what we already know about some different parts of the circle.

Diameter

The diameter is any straight line that passes through the center of the circle. It is equal to twice the radius, so:

$d = 2r$

Circumference

The circumference is the length of the path around the circle. Algebraically it is given by: 

$c = 2\pi r$ 

or equivalently by $c = \pi d$. The number $\pi$ (pi) is defined by this relationship. It is the ratio of any circle's circumference to its own diameter.

Area

The area of a circle is given by: 

$A = \pi r^2$

Notice that the radius is the only defining parameter for the size of any particular circle, and so it is the only variable that the area depends on.