Introduction to Ellipses

An ellipse is one of the shapes called conic sections, which is formed by the intersection of a plane with a right circular cone. The general equation of an ellipse centered at $\left(h,k\right)$ is:

$\displaystyle{\frac{\left(x-h\right)^2}{a^2} + \frac{\left(y-k\right)^2}{b^2} = 1}$

when the major axis of the ellipse is horizontal.

Ellipse

An ellipse is a conic section, formed by the intersection of a plane with a right circular cone.

In most definitions of the conic sections, the circle is defined as a special case of the ellipse, when the plane is parallel to the base of the cone. However, it is also possible to begin with the definition of a circle and use graphical transformations to arrive at the general formula for an ellipse.

Recall that a circle is defined as the set of all points equidistant from a common center. For simplicity, we will choose that center to be $\left(0,0\right)$, the origin of the $x$-$y$ plane. Then we can write the equation of the circle in this way:

$x^2 + y^2 = r^2$

In this equation, $r$ is the radius of the circle. A circle has only one radius—the distance from the center to any point is the same. To change our circle into an ellipse, we will have to stretch or squeeze the circle so that the distances are no longer the same. First, let's start with a specific circle that's easy to work with, the circle centered at the origin with radius $1$.

$x^2 + y^2 = 1$

To make this into an ellipse, we must distort the circular shape so that it is no longer symmetric between $x$ and $y$. To do this, we introduce a scaling factor into one or both of the $x$-$y$ coordinates. Let's start by dividing all $x$ coordinates by a factor $a$, and therefore scaling the $x$ values. We simply substitute $\displaystyle{\frac{x}{a}}$ into the equation instead of $x$. Important note: We assume that $a > 1$.

$\displaystyle{\left(\frac{x}{a}\right)^2 + y^2 = 1}$

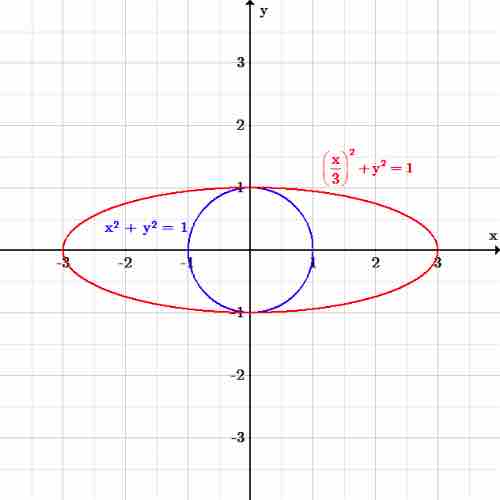
Ellipse along $x$-axis

The ellipse $\left( \frac{x}{3} \right)^2 +y^2 = 1$ has been stretched along the $x$-axis by a factor of 3 as compared to the circle $x^2 + y^2 = 1$.

Every $x$-value that solved the old equation must now be multiplied by $a$ in order to solve the new equation. This has the effect of stretching the ellipse further out on the $x$-axis, because larger values of $x$ are now the solutions. 

Similarly, we can scale all the values of $y$ by a factor $b$ (we also assume $b > 1$).

 $\displaystyle {x^2 + \left(\frac{y}{b}\right)^2 = 1}$

Now all the $y$ values are stretched vertically, further away from the origin. 

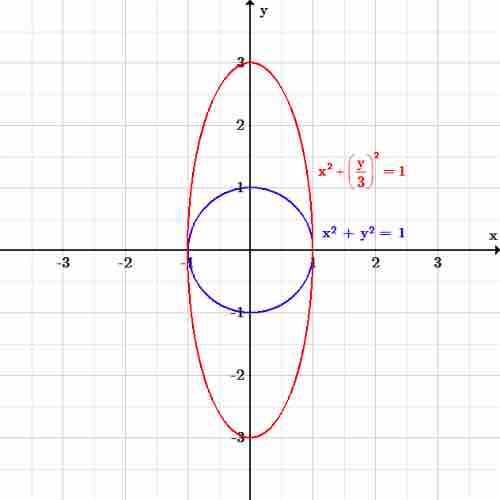
Ellipse along $y$-axis

The ellipse $x^2 +\left( \frac{y}{3} \right)^2 = 1$ has been stretched along the $y$-axis by a factor of 3 as compared to the circle $x^2 + y^2 = 1$.

If we stretch in both the $x$ and $y$ directions and distribute the powers of two through the parentheses, we get:

$\displaystyle{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1}$

which is exactly the equation of a horizontal ellipse centered at the origin. 

If we had used scaling factors that were less than one, it would have compressed the shape instead of stretching it further out.