Further Transcendental Functions

A transcendental function is a function that is not algebraic. Such a function cannot be expressed as a solution of a polynomial equation whose coefficients are themselves polynomials with rational coefficients. Examples of transcendental functions include the exponential function, the logarithm, and the trigonometric functions.

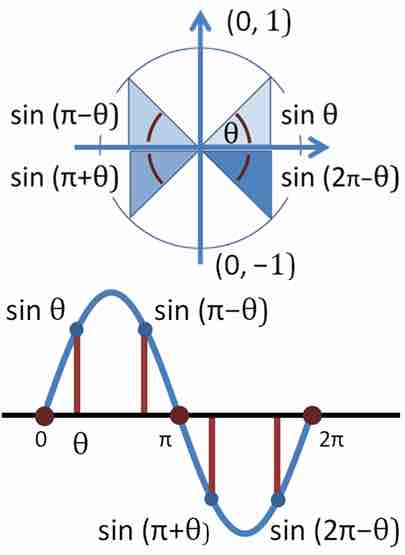
Trigonometric Functions

Top panel: Trigonometric function sinθ for selected angles $\theta$, $\pi - \theta$, $\pi + \theta$, and $2\pi - \theta$ in the four quadrants. Bottom panel: Graph of sine function versus angle.

Formally, an analytic function $ƒ(z)$ of the real or complex variables $z_1, \cdots ,z_n$ is transcendental if $z_1, \cdots ,z_n$, $ƒ(z)$ are algebraically independent, i.e., if $ƒ$ is transcendental over the field $C(z_1, \cdots ,z_n)$.

A transcendental function is a function that "transcends" algebra in the sense that it cannot be expressed in terms of a finite sequence of the algebraic operations of addition, multiplication, power, and root extraction.

The following functions are transcendental:

$f_1(x) = x^{\Pi }$

$f_2(x) = c^{x }, x \neq 0, 1$

$f_3(x) = x^{x}$

$f_4(x) = x^{\frac{1}{x}}$

$f_5(x) = \log_{c}(x)$

$f_6(x) = \sin(x)$

Note that, for $ƒ_2$ in particular, if we set $c$ equal to $e$, the base of the natural logarithm, then we find that $e^x$ is a transcendental function. Similarly, if we set $c$ equal to $e$ in ƒ₅, then we find that $\ln(x)$, the natural logarithm, is a transcendental function.

In dimensional analysis, transcendental functions are notable because they make sense only when their argument is dimensionless (possibly after algebraic reduction). Because of this, transcendental functions can be an easy-to-spot source of dimensional errors. For example, $\log(5 \text{ meters})$ is a nonsensical expression, unlike $\log \left ( \frac{5 \text{ meters}}{3 \text{ meters}} \right )$ or $\log(3)\text{ meters}$. One could attempt to apply a logarithmic identity to get $\log(10) + \log(m)$, which highlights the problem: applying a non-algebraic operation to a dimension creates meaningless results.