Null Measurements
Standard measurements of voltage and current alter circuits, introducing numerical uncertainties. Voltmeters draw some extra current, whereas ammeters reduce current flow. Null measurements balance voltages, so there is no current flowing through the measuring device and the circuit is unaltered. Null measurements are generally more accurate but more complex than standard voltmeters and ammeters. Their precision is still limited.
The Potentiometer
When measuring the EMF of a battery and connecting the battery directly to a standard voltmeter, as shown in , the actual quantity measured is the terminal voltage V. Voltage is related to the EMF of the battery by V=emf−Ir, where I is the current that flows and r is the internal resistance of the battery.
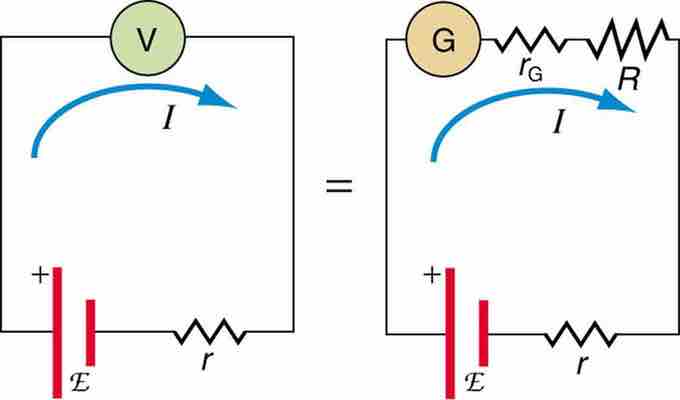
Voltmeter Connected to Battery
An analog voltmeter attached to a battery draws a small but nonzero current and measures a terminal voltage that differs from the EMF of the battery. (Note that the script capital E symbolizes electromotive force, or EMF. ) Since the internal resistance of the battery is not known precisely, it is not possible to calculate the EMF precisely.
The EMF could be accurately calculated if r were known, which is rare. If the current I could be made zero, then V=emf, and EMF could be directly measured. However, standard voltmeters need a current to operate.
A potentiometer is a null measurement device for measuring potentials (voltages). A voltage source is connected to resistor R, passing a constant current through it. There is a steady drop in potential (IR drop) along the wire, so a variable potential is obtained through contact along the wire.
An unknown emfx (represented by script Ex) connected in series with a galvanometer is shown in . Note that emfx opposes the other voltage source. The location of the contact point is adjusted until the galvanometer reads zero. When the galvanometer reads zero, emfx=IRx, where Rxis the resistance of the wire section up to the contact point. Since no current flows through the galvanometer, none flows through the unknown EMF, and emfx is sensed.
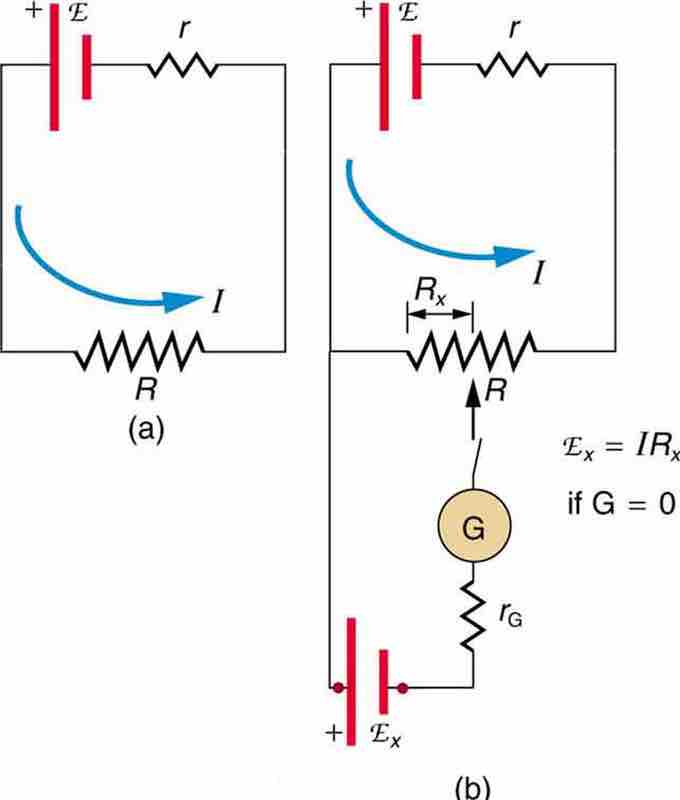
Potentiometer
The potentiometer is a null measurement device. (a. ) A voltage source connected to a long wire resistor passes a constant current I through it. (b.) An unknown EMF (labeled script Ex) is connected as shown, and the point of contact along R is adjusted until the galvanometer reads zero. The segment of wire has a resistance Rx and script Ex=IRx, where I is unaffected by the connection, since no current flows through the galvanometer. The unknown EMF is thus proportional to the resistance of the wire segment.
Standard EMF is substituted for emfx, and the contact point is adjusted until the galvanometer reads zero, so that emfs=IRs. In both cases, no current passes through the galvanometer. The current I through the long wire is identical. Taking the ratio emfx/emfs, I cancels, and solving for emfx gives what is seen in .
Because a long uniform wire is used for R, the ratio of resistances Rx/Rs is the same as the ratio of the lengths of wire that zero the galvanometer for each EMF. The three quantities on the right-hand side of the equation are now known or measured, and emfx can be calculated. There is often less uncertainty in this calculation than when using a voltmeter directly, but it is not zero. There is always some uncertainty in the ratio of resistances Rx/Rsand in the standard EMFs. Furthermore, it is not possible to tell when the galvanometer reads exactly zero, which introduces error into both Rx and Rs, and may also affect the current I.
Resistance Measurements
Many so-called ohmmeters measure resistance. Most common ohmmeters apply a voltage to a resistance, measure the current, and calculate the resistance using Ohm's law. Their readout is this calculated resistance. Simple configurations using standard voltmeters and ammeters have limited accuracy, because the meters alter both the voltage applied to the resistor and the current flowing through it. The Wheatstone bridge is a null measurement device for calculating resistance by balancing potential drops in a circuit. The device is called a bridge because the galvanometer forms a bridge between two branches. A variety of bridge devicesare used to make null measurements in circuits . Resistors R1 and R2 are precisely known, while the arrow through R3indicates that it is a variable resistance. The value of R3 can be precisely read. With the unknown resistance Rx in the circuit, R3 is adjusted until the galvanometer reads zero.
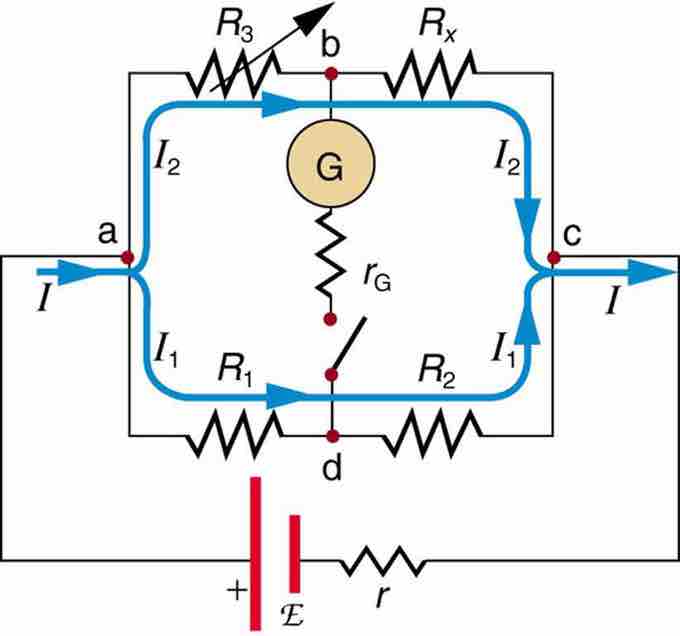
Wheatstone Bridge
The Wheatstone bridge is used to calculate unknown resistances. The variable resistance R3 is adjusted until the galvanometer reads zero with the switch closed. This simplifies the circuit, allowing Rx to be calculated based on the IR drops.
The potential difference between points b and d is then zero, meaning that b and d are at the same potential. With no current running through the galvanometer, it has no effect on the rest of the circuit. So the branches abc and adc are in parallel, and each branch has the full voltage of the source. Since b and d are at the same potential, the IR drop along ad must equal the IR drop along ab. Again, since b and d are at the same potential, the IR drop along dc must equal the IR drop along bc. This equation is used to calculate the unknown resistance when current through the galvanometer is zero. This method can be very accurate, but it is limited by two factors. First, it is not possible for the current through the galvanometer to be exactly zero. Second, there are always uncertainties in R1, R2, and R3, which contribute to the uncertainty in Rx.