Use of Vectors
Vectors can be used to represent physical quantities. Most commonly in physics, vectors are used to represent displacement, velocity, and acceleration. Vectors are a combination of magnitude and direction, and are drawn as arrows. The length represents the magnitude and the direction of that quantity is the direction in which the vector is pointing. Because vectors are constructed this way, it is helpful to analyze physical quantities (with both size and direction) as vectors.
Applications
In physics, vectors are useful because they can visually represent position, displacement, velocity and acceleration. When drawing vectors, you often do not have enough space to draw them to the scale they are representing, so it is important to denote somewhere what scale they are being drawn at. For example, when drawing a vector that represents a magnitude of 100, one may draw a line that is 5 units long at a scale of
Position and Displacement
Displacement is defined as the distance, in any direction, of an object relative to the position of another object. Physicists use the concept of a position vector as a graphical tool to visualize displacements. A position vector expresses the position of an object from the origin of a coordinate system. A position vector can also be used to show the position of an object in relation to a reference point, secondary object or initial position (if analyzing how far the object has moved from its original location). The position vector is a straight line drawn from the arbitrary origin to the object. Once drawn, the vector has a length and a direction relative to the coordinate system used.
Velocity
Velocity is also defined in terms of a magnitude and direction. To say that something is gaining or losing velocity one must also say how much and in what direction. For example, an airplane flying at 200
Acceleration
Acceleration, being the time rate of change of velocity, is composed of a magnitude and a direction, and is drawn with the same concept as a velocity vector. A value for acceleration would not be helpful in physics if the magnitude and direction of this acceleration was unknown, which is why these vectors are important. In a free body diagram, for example, of an object falling, it would be helpful to use an acceleration vector near the object to denote its acceleration towards the ground. If gravity is the only force acting on the object, this vector would be pointing downward with a magnitude of 9.81
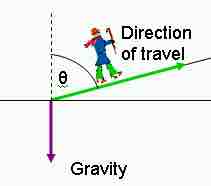
Vector Diagram
Here is a man walking up a hill. His direction of travel is defined by the angle theta relative to the vertical axis and by the length of the arrow going up the hill. He is also being accelerated downward by gravity.