Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses, and inversely proportional to the square of the distance between them.
In modern language, the law states the following: Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them:
where
If the bodies in question have spatial extent (rather than being theoretical point masses), then the gravitational force between them is calculated by summing the contributions of the notional point masses which constitute the bodies. In the limit, as the component point masses become "infinitely small", this entails integrating the force (in vector form, see below) over the extents of the two bodies.
In this way it can be shown that an object with a spherically-symmetric distribution of mass exerts the same gravitational attraction on external bodies as if all the object's mass were concentrated at a point at its center.
For points inside a spherically-symmetric distribution of matter, Newton's Shell theorem can be used to find the gravitational force. The theorem tells us how different parts of the mass distribution affect the gravitational force measured at a point located a distance
- The portion of the mass that is located at radii
$r<r_0$ causes the same force at$r_0$ as if all of the mass enclosed within a sphere of radius$r_0$ was concentrated at the center of the mass distribution (as noted above). - The portion of the mass that is located at radii
$r>r_0$ exerts no net gravitational force at the distance$r_0$ from the center. That is, the individual gravitational forces exerted by the elements of the sphere out there, on the point at$r_0$ , cancel each other out.
As a consequence, for example, within a shell of uniform thickness and density there is no net gravitational acceleration anywhere within the hollow sphere. Furthermore, inside a uniform sphere the gravity increases linearly with the distance from the center; the increase due to the additional mass is 1.5 times the decrease due to the larger distance from the center. Thus, if a spherically symmetric body has a uniform core and a uniform mantle with a density that is less than
The gravity of the Earth may be highest at the core/mantle boundary, as shown in Figure 1:
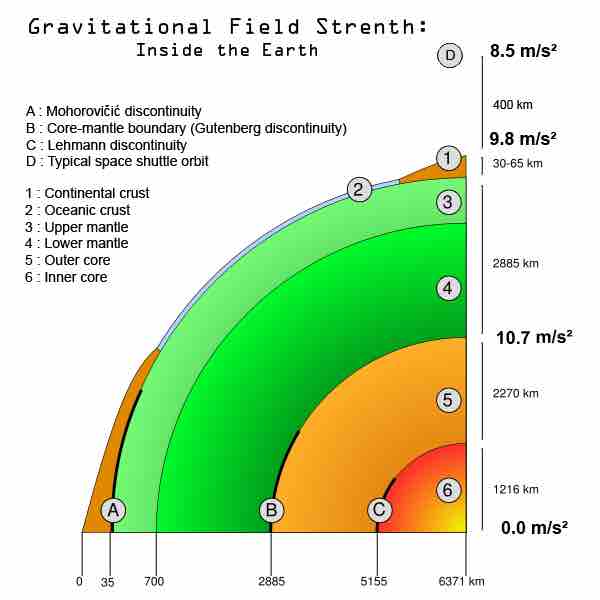
Gravitational Field of Earth
Diagram of the gravitational field strength within the Earth.