The human mind is a problem-solving machine. You may not realize it, but as you walk through the world, you are solving problems every second—everything from "I'm running late, what's the quickest way for me to get to class?" to "Where did I leave my wallet?" to "What should my psychology paper be about?"

In psychology, "problem solving" refers to a way of reaching a goal from a present condition, where the present condition is either not directly moving toward the goal, is far from it, or needs more complex logic in order to find steps toward the goal. It is considered the most complex of all intellectual functions, since it is a higher-order cognitive process that requires the modulation and control of basic skills. There are considered to be two major domains in problem solving: mathematical problem solving, which involves problems capable of being represented by symbols, and personal problem solving, where some difficulty or barrier is encountered.

Barriers to Problem Solving

There are many common mental constructs that impede our ability to correctly solve problems in the most efficient manner possible. 

Mental Set and Functional Fixedness

A mental set is an unconscious tendency to approach a problem in a particular way. Our mental sets are shaped by our past experiences and habits. For example, if the last time your computer froze you restarted it and it worked, that might be the only solution you can think of the next time it freezes.

Functional fixedness is a special type of mental set that occurs when the intended purpose of an object hinders a person's ability to see its potential other uses. So for example, say you need to open a can of broth but you only have a hammer. You might not realize that you could use the pointy, two-pronged end of the hammer to puncture the top of the can, since you are so accustomed to using the hammer as simply a pounding tool.

Unnecessary Constraints

The dot problem

In the dot problem, described below, solvers must attempt to connect all nine dots with no more than four lines, without lifting their pen from the paper. 

This is a barrier that shows up in problem solving that causes people to unconsciously place boundaries on the task at hand. A famous example of this barrier to problem solving is the dot problem. In this problem, there are nine dots arranged in a 3 x 3 square. The solver is asked to draw no more than four lines, without lifting their pen or pencil from the paper, that connect all of the dots. What often happens is that the solver creates an assumption in their mind that they must connect the dots without letting the lines go outside the square of dots. The solvers are literally unable to think outside the box. Standardized procedures of this nature often involve mentally invented constraints of this kind.

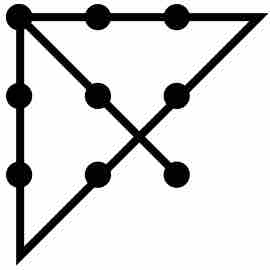
The dot problem's solution

Most solvers do not recognize that they can go outside the box and draw longer lines to connect the dots.

Irrelevant Information

Irrelevant information is information that is presented as part of a problem, but which is unrelated or unimportant to that problem and will not help solve it. Typically, it detracts from the problem-solving process, as it may seem pertinent and distract people from finding the most efficient solution. An example of a problem hindered by irrelevant information is this: 

15% of people in Topeka have unlisted telephone numbers. You select 200 names at random from the Topeka phone book. How many of these people have unlisted phone numbers?

The answer, of course, is none of them: if they are in the phone book, they do not have unlisted numbers. But the extraneous information at the beginning of the problem makes many people believe they have to perform a mathematical calculation of some sort. This is the trouble that irrelevant information can cause.

Problem-Solving Strategies

There are many strategies that can make solving a problem easier and more efficient. Two of them, algorithms and heuristics, are of particularly great psychological importance.

Heuristic

A heuristic is a rule of thumb, a strategy, or a mental shortcut that generally works for solving a problem (particularly decision-making problems). It is a practical method, one that is not a hundred percent guaranteed to be optimal or even successful, but is sufficient for the immediate goal. The advantage of heuristics is that they often reduce the time and cognitive load required to solve a problem; the disadvantage is that they cannot always be relied on to solve the problem—just most of the time. 

Algorithm

An algorithm is a series of sets of steps for solving a problem. Unlike a heuristic, you are guaranteed to get the correct solution to the problem; however, an algorithm may not necessarily be the most efficient way of solving the problem. Additionally, you need to know the algorithm (i.e., the complete set of steps), which is not usually realistic for the problems of daily life.

The difference between an algorithm and a heuristic can be summed up in the example of trying to find a Starbucks (or some other national chain) in a city. An algorithm would be a series of steps: "Walk in an increasingly large grid pattern around the city blocks until you find a Starbucks or you have looked at every street." But a heuristic could simply be, "Well, usually they're at busy intersections; I'll just walk to the nearest busy intersection."

Other Strategies

There are many other ways of solving a problem. The most effective depends on the type of problem and the resources at hand.

• Abstraction: solving the problem in a model of the system before applying it to the real system.
• Analogy: using a solution for a similar problem.
• Brainstorming: suggesting a large number of solutions and developing them until the best is found.
• Divide and conquer: breaking down a large, complex problem into smaller, solvable problems.
• Hypothesis testing: assuming a possible explanation to the problem and trying to prove (or, in some contexts, disprove) the assumption.
• Lateral thinking: approaching solutions indirectly and creatively.
• Means-ends analysis: choosing an action at each step to move closer to the goal.
• Morphological analysis: assessing the output and interactions of an entire system.
• Proof: try to prove that the problem cannot be solved. The point where the proof fails will be the starting point for solving it.
• Reduction: transforming the problem into another problem for which solutions exist.
• Root-cause analysis: identifying the cause of a problem.
• Trial and error: testing possible solutions until the right one is found.