The interquartile range (IQR) is a measure of statistical dispersion, or variability, based on dividing a data set into quartiles. Quartiles divide an ordered data set into four equal parts. The values that divide these parts are known as the first quartile, second quartile and third quartile (Q1, Q2, Q3). The interquartile range is equal to the difference between the upper and lower quartiles:
IQR = Q3 − Q1
It is a trimmed estimator, defined as the 25% trimmed mid-range, and is the most significant basic robust measure of scale. As an example, consider the following numbers:
1, 13, 6, 21, 19, 2, 137
Put the data in numerical order: 1, 2, 6, 13, 19, 21, 137
Find the median of the data: 13
Divide the data into four quartiles by finding the median of all the numbers below the median of the full set, and then find the median of all the numbers above the median of the full set.
To find the lower quartile, take all of the numbers below the median: 1, 2, 6
Find the median of these numbers: take the first and last number in the subset and add their positions (not values) and divide by two. This will give you the position of your median:
1+3 = 4/2 = 2
The median of the subset is the second position, which is two. Repeat with numbers above the median of the full set: 19, 21, 137. Median is 1+3 = 4/2 = 2nd position, which is 21. This median separates the third and fourth quartiles.
Subtract the lower quartile from the upper quartile: 21-2=19. This is the Interquartile range, or IQR.
If there is an even number of values, then the position of the median will be in between two numbers. In that case, take the average of the two numbers that the median is between. Example: 1, 3, 7, 12. Median is 1+4=5/2=2.5th position, so it is the average of the second and third positions, which is 3+7=10/2=5. This median separates the first and second quartiles.
Uses
Unlike (total) range, the interquartile range has a breakdown point of 25%. Thus, it is often preferred to the total range. In other words, since this process excludes outliers, the interquartile range is a more accurate representation of the "spread" of the data than range.
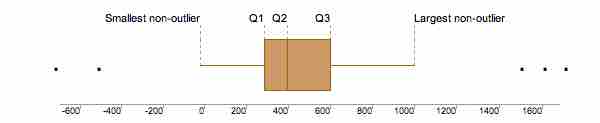
The IQR is used to build box plots, which are simple graphical representations of a probability distribution. A box plot separates the quartiles of the data. All outliers are displayed as regular points on the graph. The vertical line in the box indicates the location of the median of the data. The box starts at the lower quartile and ends at the upper quartile, so the difference, or length of the boxplot, is the IQR.
On this boxplot in , the IQR is about 300, because Q1 starts at about 300 and Q3 ends at 600, and 600 - 300 = 300.
Interquartile Range
The IQR is used to build box plots, which are simple graphical representations of a probability distribution.
In a boxplot, if the median (Q2 vertical line) is in the center of the box, the distribution is symmetrical. If the median is to the left of the data (such as in the graph above), then the distribution is considered to be skewed right because there is more data on the right side of the median. Similarly, if the median is on the right side of the box, the distribution is skewed left because there is more data on the left side.
The range of this data is 1,700 (biggest outlier) - 500 (smallest outlier) = 2,200. If you wanted to leave out the outliers for a more accurate reading, you would subtract the values at the ends of both "whiskers:"
1,000 - 0 = 1,000
To calculate whether something is truly an outlier or not you use the formula 1.5 x IQR. Once you get that number, the range that includes numbers that are not outliers is [Q1 - 1.5(IQR), Q3 + 1.5(IQR)]. Anything lying outside those numbers are true outliers.