Fracciones equivalentes |

1.- Fracciones equivalentes.
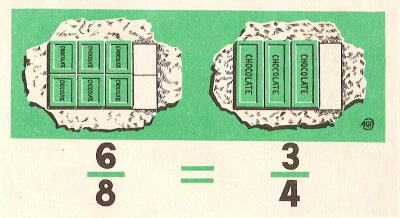
A Montse le han dado 6/8 de la tableta de chocolate de la izquierda y a Juan 3/4 de tableta del dibujo de la derecha. Ambos han recibido la misma cantidad de chocolate.
Si los dos términos de una fracción los multiplicamos por 2, su valor no varía. 3/4 = 3x2/4x2 = 6/8.
De la misma forma podemos decir que al dividir los dos términos de una fracción por un número su valor no se altera.
Ejemplo: 6/8 = 6:2/8:2 = 3/4.
Contesta a estas cuestiones: