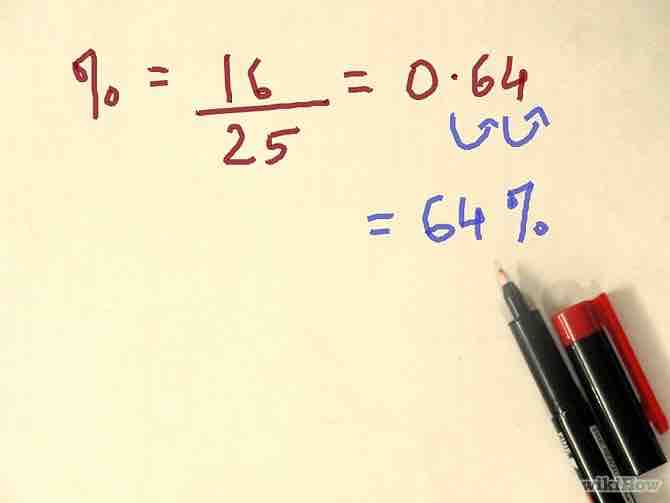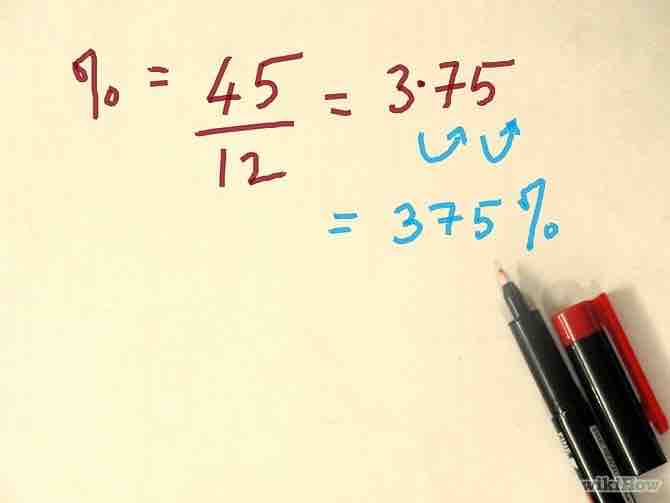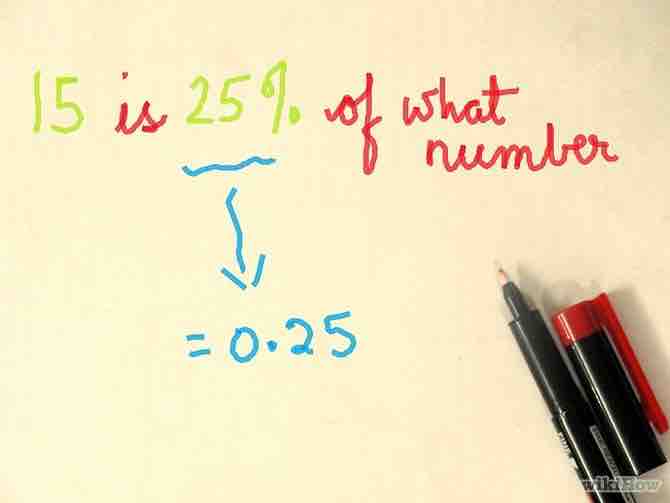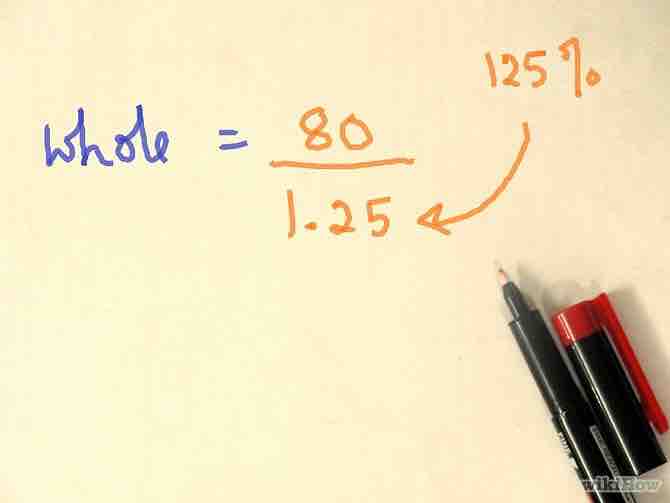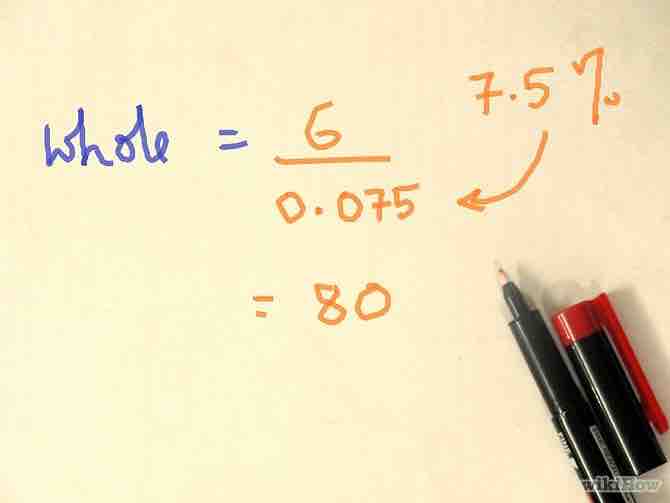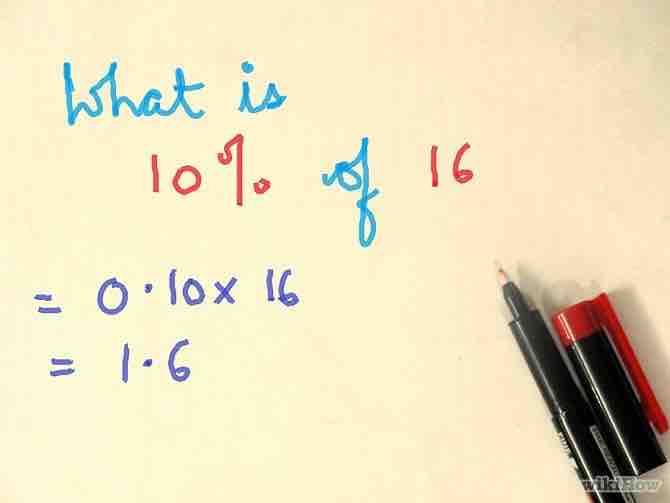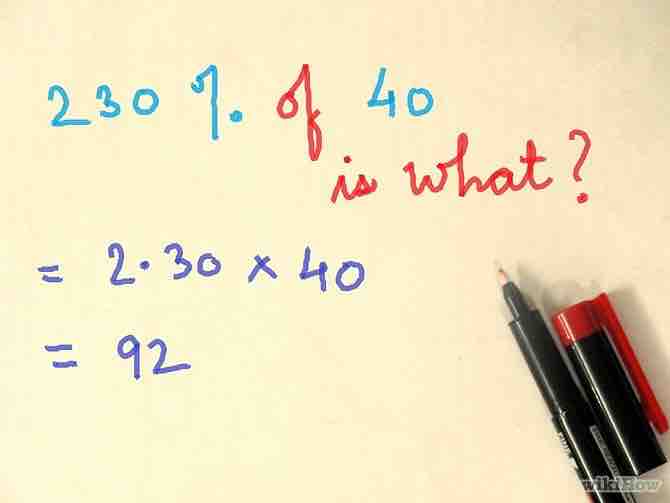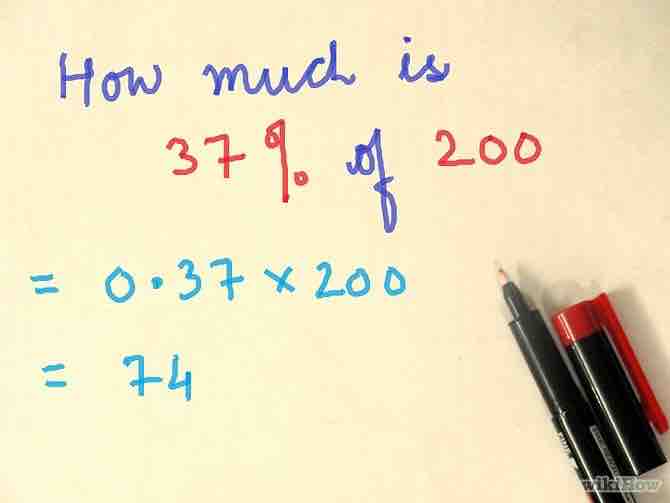Cómo trabajar con porcentajes

3 métodos:Resuelve un problema de "porcentaje desconocido"Resuelve un problema de "Cantidad total desconocida"Resuelve un problema de "cantidad parcial desconocida"

La primera cosa que debes entender es que existen "dos grandes categorías" en los problemas de porcentajes: las preguntas de comparación directa (tal como, "¿35 es el 5% de cual número?") y preguntas de aumento o decremento (como, "Si una blusa que originalmente cuesta $45 tiene un descuento de 20%, ¿cuál es el precio total?). Los problemas de aumento o decremento son un poco complicados, y por ello se tratarán en otro artículo de Wikihow, así que únicamente nos enfocaremos con las comparaciones directas en este artículo.

La otra cosa que debes saber es que hay dos maneras de abordar este tipo de preguntas. Una se basa en una ecuación que utiliza decimales y la otra usa proporciones. Vamos a utilizar el método que se basa en la ecuación decimal, la cual es: % x (cantidad total) = (cantidad parcial). Esta ecuación puede reacomodarse de la siguiente manera: % = (cantidad parcial) / (cantidad total). También puede escribirse así: (cantidad total) = (cantidad parcial) / %. El orden que se necesite depende del tipo de problema que tienes.

Anuncio

Donde comenzar

Tu primer objetivo es "entender qué tipo de problema es." En una situación de comparación directa, existen "tres estilos" de problema. El primer estilo es la pregunta de "no porcentaje". Son aquellos que suenan así: "¿Qué porcentaje de 25 es 16?" o "¿8 es qué porcentaje de 32?". El segundo estilo es el de "no hay cantidad completa " . Estos se escriben así: "¿15 es el 6% de cuál número?" o "¿20 es el 78% de cuál número?". El tercer estilo es el de "sin cantidad parcial" , que suena como: "¿Cuál es el 52% de 49?" o "¿Cuánto es el 14% de 225?"

Método 1 de 3: Resuelve un problema de "porcentaje desconocido"

Si no ves un número marcado con el signo de % (o posiblemente la palabra "porcentaje"), entonces esta es el tipo de pregunta de "sin porcentaje".

1
Decide cual de los otros números es la "cantidad total" y cual es la "cantidad parcial". Por ejemplo, un problema que dice "¿8 es qué porcentaje de 32?" indica que 32 es la cantidad total y 8 es la parcial. Para entenderlo: el 8 se conecta directamente con el "es", mientras que el 32 se conecta directamente con el "de".

Anuncio
2
Usa la ecuación % = (parcial)/(total). Así que en la calculadora, coloca la cantidad parcial, presiona dividir, e ingresa el total y presiona igual.
3
Esto te dará un decimal, el cual puedes convertir en un porcentaje al mover el punto decimal dos lugares a la derecha.
- Ejemplo: "¿Cuál porcentaje es 8 de 32?". Toma el 8, divide por 32, presiona igual; te da 0.25; conviertelo a 25%.
- Ejemplo: "¿Cuál porcentaje de 25 es 16?". Ingresa 16, divide por 25, presiona igual; te da 0.64; convierte a 64%.
- Ejemplo: "¿Cuál porcentaje de 12 es 45?". Ingresa 45, divide por 12, presiona igual; te da 3.75; convierte a 375%. (Las respuestas mayores que 100%, si bien son raras, son aceptables).
- Ejemplo: "¿9 es cuál porcentaje de 250?". Ingresa 9, divide por 250, presiona igual; te da 0.036; convierte a 3.6%.
Anuncio

Método 2 de 3: Resuelve un problema de "Cantidad total desconocida"

Vamos a decir que tienes un porcentaje. Ahora tienes que decidir si la pregunta es del tipo de "sin cantidad total" o el tipo de "cantidad parcial desconocida". Esta pregunta es difícil de responder y depende del contexto de la pregunta.

1
Busca los marcadores "es" y "de" y "qué o cuál". "Es" tiende a estar asociado con la cantidad parcial, mientras "de" se relaciona con la cantidad total. La palabra "qué o cuál" indica el elemento desconocido.
- Ejemplo: una pregunta dice, "¿Cuál es el 10% de 16?" La frase "cuál es" indica que la cantidad parcial es desconocida. La frase "de 16" indica que 16 es la cantidad total. Este es un problema de "cantidad parcial desconocida".
- Ejemplo: Una pregunta dice, "¿15 es el 25% de cuál número?" La frase "de cuál" significa que la cantidad total es desconocida, pero la frase "15 es" demuestra que 15 es la cantidad parcial. Este sería un problema de "cantidad total desconocida".
2
Vamos a asumir que el problema es de "cantidad total desconocida", como "¿15 es 25% de cuál número?". Primero que nada, cambia el porcentaje a decimal --- 0.25 en lugar de 25%, 1.38 en lugar de 138%, 0.07 en lugar de 7%, etc.
3
Usa la ecuación: (cantidad total) = (parcial) / %.
4
Utiliza tu calculadora, para ingresar la cantidad parcial, presiona dividir, ingresa el porcentaje decimal, y presiona igual.
- Ejemplo: "¿15 es el 25% de cuál número?". Toma tu calculadora, ingresa 15, presiona la tecla de dividir, ingresa 0.25, presiona igual. La respuesta es 60. Haz terminado. (Observa, es solamente 60. No 60%.)
- Ejemplo: "¿32% de cuál número es 16?". Ingresa 16, presiona dividir, ingresa 0.32, presiona igual; la respuesta es 50.
- Ejemplo: "¿125% de cuál número es 80?". Ingresa 80, presiona dividir, ingresa 1.25, presiona igual; la respuesta es 64.
- Ejemplo: "¿6 es 7.5% de cuál número?". Ingresa 6, presiona dividir, ingresa .075, presiona igual; la respuesta es 80.
Anuncio

Método 3 de 3: Resuelve un problema de "cantidad parcial desconocida"

1
Busca el "es", "de", y "qué o cuál" (o posiblemente "cuánto"). Si el "es" y el "qué o cuál" están asociados de cerca, como en la pregunta "¿Cuál es 10% de 16?", entonces tienes un problema de "sin cantidad parcial".
2
Esto es lo que hay que hacer: Cambia el porcentaje a decimal, así 32% es 0.32 y 75% es 0.75 y 150% es 1.5 y 6% es 0.06, etc.
3
Usa la ecuación: % x (cantidad total) = (cantidad parcial). En otras palabras, multiplica el porcentaje de cantidades completas.
- Ejemplo: "¿Cuál es el 10% de 16?". Ingresa 0.10, presiona multiplicar, ingresa 16, presiona igual. La respuesta es 1.6 (observa, no hay un signo de % en la respuesta).
- Ejemplo: "¿230% de 40 es qué cantidad?". Ingresa 2.3, presiona multiplicar, ingresa 40, presiona igual. La respuesta: 92.
- Ejemplo: "¿Cuánto es 37% de 200?". Ingresa 0.37, presiona multiplicar, ingresa 200, presiona igual. Respuesta: 74.
Anuncio

Consejos

En resumen, puedes: A) dividir el parcial POR el total; o, B) dividir el parcial POR el porcentaje; o, C) multiplicar el total por el porcentaje. El que decidas utilizar depende de cuáles números tienes.
El único momento donde debes multiplicar es si tienes el % y la cantidad total. De otra manera, debes dividir.
Aplica el principio de "Eso parece correcto". Asegúrate de que tu respuesta sea racional.
Con el estilo de problema de "sin cantidad parcial", el orden de la multiplicación no importa. Puedes resolver "230% de 45" con la secuencia 2.3 x 45= o con 45 x 2.3 =

Anuncio

Advertencias

¡El orden de la división es vitalmente importante! En ambos tipos de preguntas que se resuelven en la división, la "cantidad parcial se pone primero en la calculadora."
La mayoría de las calculadoras tienen una tecla de porcentaje. Su propósito es mover el punto decimal dos veces hacia la izquierda, para convertir 35% en 0.35, y 325% en 3.25, y 6% en 0.06. No te recomiendo que uses esta tecla porque he visto que los estudiantes mueven el punto decimal ellos mismos, y cuando presionan el signo de % también, todo se revuelve.