
/pt/multiplos-e-divisores/decomposicao-em-fatores-primos/content/
Por conta da importância da decomposição em fatores primos ou decomposição prima, é necessário saber como calculá-la. Vejamos neste exemplo como encontrar a decomposição prima de .
Primeiros escrevemos o número que será decomposto e ao lado traçamos uma linha reta vertical como mostra a imagem abaixo:

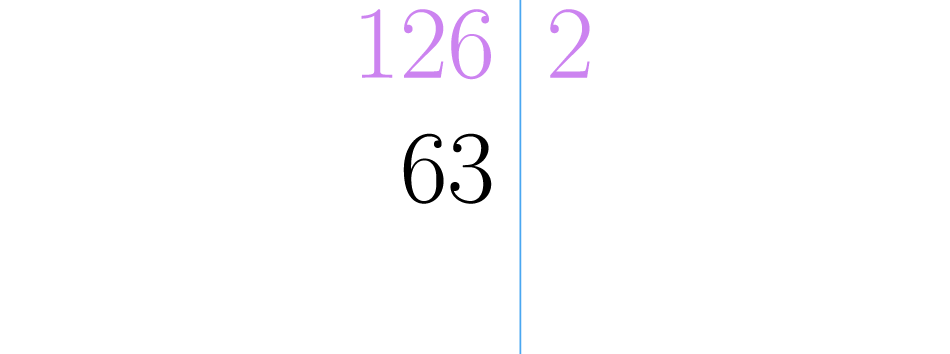
Começamos tentando com o e como é divisor de , escrevemos do outro lado da linha e fazemos a divisão . Em seguida colocamos o resultado embaixo do , como mostramos na figura.
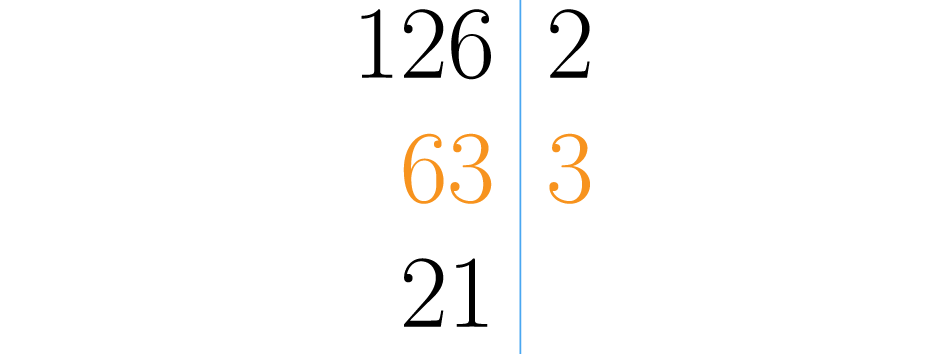
Tentamos então com próximo número primo: o . Três é divisor de assim o escrevemos à direita da linha, debaixo do e fazemos a divisão , colocando o resultado debaixo do .
Agora temos que dividir entre o menor número primo possível onde o resultado será novamente o . Escrevemos outro à direita da linha, embaixo dos outros números primos que usamos. Fazemos a divisão , e colocamos o resultado à esquerda da linha, embaixo do , para repetir o processo.
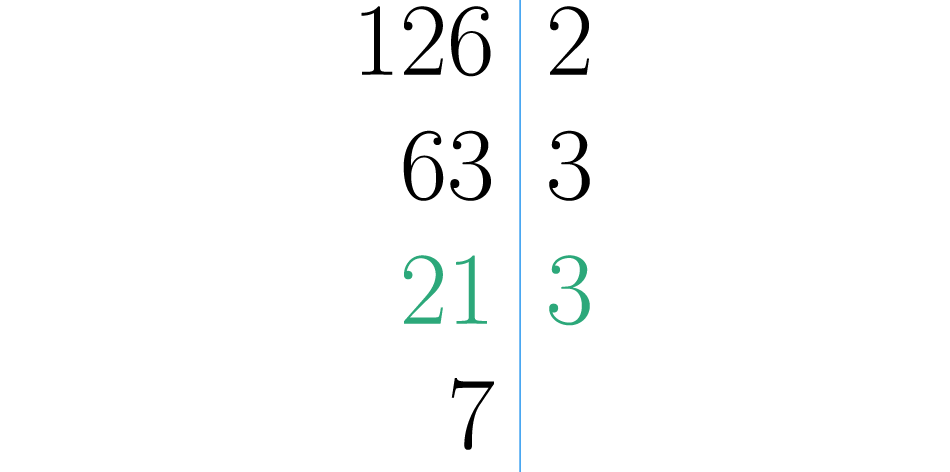
Agora devemos encontrar o menor número primo possível que divida o , mas como é um número primo, só serve ele mesmo.
Escrevemos o sete à direita da linha e fazemos a operação . Em seguida colocamos o resultado da divisão à esquerda da linha, embaixo do :
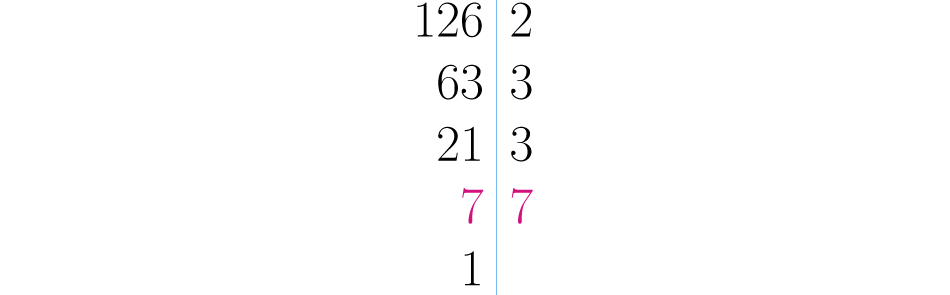
Quando obtemos o quociente na parte esquerda, consideramos o processo terminado. A decomposição que buscamos é o produto ou a multiplicação dos números primos usados no processo, ou seja, os números que ficaram escritos à direita da linha. Podemos afirmar assim que , ou que é igual: .
/pt/multiplos-e-divisores/a-decomposicao-prima-e-os-divisores/content/