
/pt/usando-a-matematica/os-numeros-binarios/content/
Talvez em alguma ocasião você já se perguntou qual era o tamanho do planeta Terra. O que você faria se fosse desafiado a medi-lo com seus próprios esforços? Sim, e isso significa que você não poderá usar o Google Earth, GPS, ou qualquer outra ferramenta tecnológica, acha que é possível descobrir essa medida? Acontece que um homem muito inteligente chamado Eratóstenes conseguiu descobrir e isso há mais de 2200 anos atrás! Neste texto vamos lhe explicar tudo, confira!
Começaremos revendo um conceito matemático simples. Lembre-se de que duas linhas ou retas são paralelas se não são cortados em nenhum ponto, isto é, se têm a mesma direção. Na imagem à direita você pode ver as retas de e , que são paralelas.
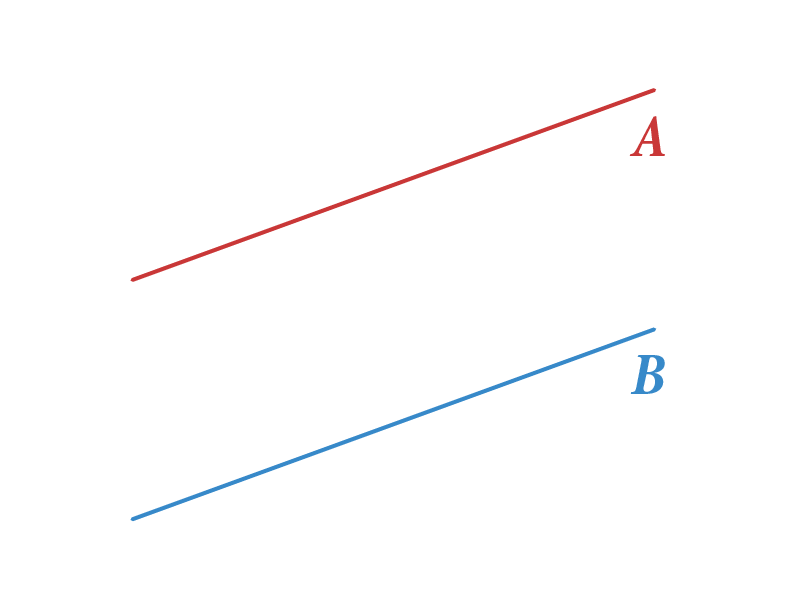
Agora traçamos uma reta que corta nossas retas paralelas e como resultado disso se formam vários ângulos como mostramos na figura.
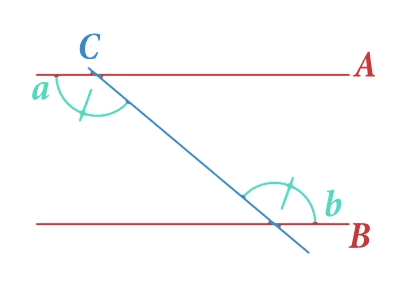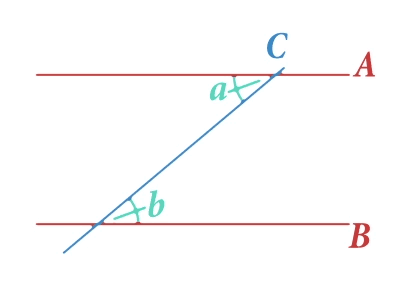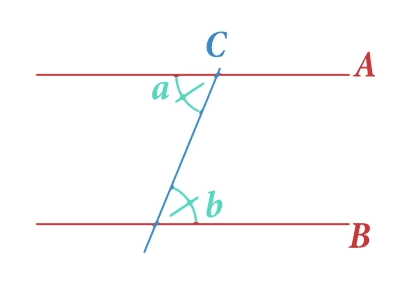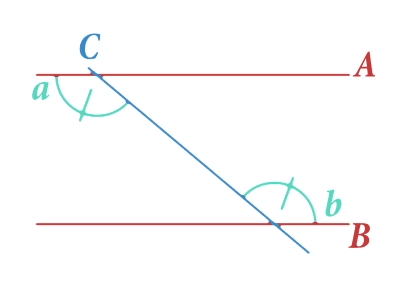
Na imagem anterior destacamos dois ângulos marcados com as letras e , que chamaremos de ângulos internos alternados. Há um princípio geométrico que afirma a igualdade destes dois ângulos. Isto é, qualquer que seja a inclinação da reta a medida dos ângulos e sempre será igual. Isso nos ajudará a entender como Eratóstenes conseguiu cumprir seu desejo. Vejamos quem foi esse ilustre personagem e como ele fez isso.
Eratóstenes nasceu na cidade grega de Cirene, atualmente Líbia no ano 276 aC. Estudou em Alexandria e em Atenas, onde se destacou por sua grande capacidade intelectual. Dominava perfeitamente matérias, como a astronomia, matemática, poesia, geografia, história e filosofia, entre outras. Foi chamado de beta (), a segunda letra do alfabeto grego, porque foi considerada o segundo melhor aluno em todas estas disciplinas. Em 236 aC foi nomeado como diretor da famosa biblioteca de Alexandria, posição que ocupou até sua morte por inanição voluntária, em 194 aC.
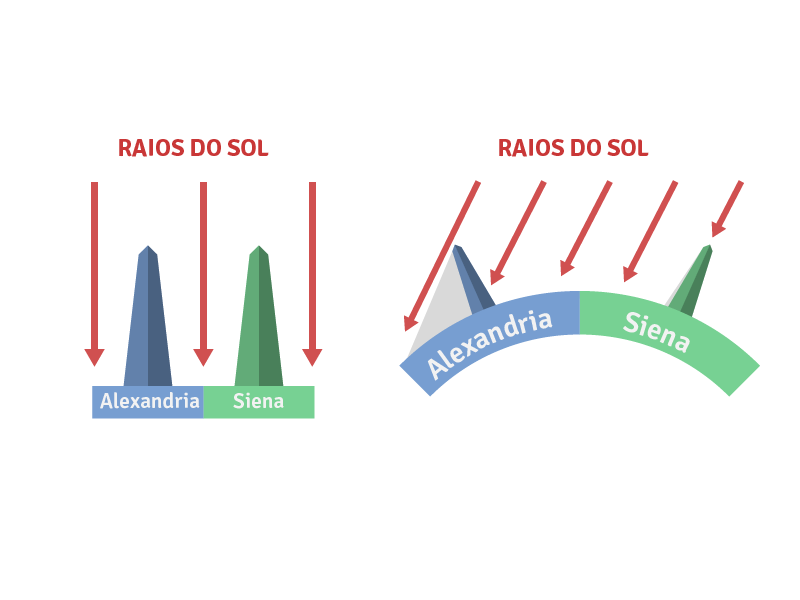
Enquanto Eratóstenes estudava alguns pergaminhos da biblioteca, descobriu que na antiga cidade de Siena (agora Aswan, Egito), nos solstícios de verão ao meio-dia exatamente as sombras não eram projetadas. No entanto, este fenômeno não acontecia em Alexandria, pois lá as sombras eram projetadas ao meio-dia nos solstícios. Este fato sugeriu a Eratóstenes que a Terra era redonda e não plana como se acreditava até então, pois se fosse plana em Alexandria também não poderia haver projeção de sombras naquele momento.
Foi neste momento que Eratóstenes usou toda a sua criatividade, pondo um pequeno pedaço de pau da forma mais vertical possível no chão na cidade de Alexandria. Ao meio-dia do solstício de verão mediu a sombra que este projetava como mostramos na figura ao lado.
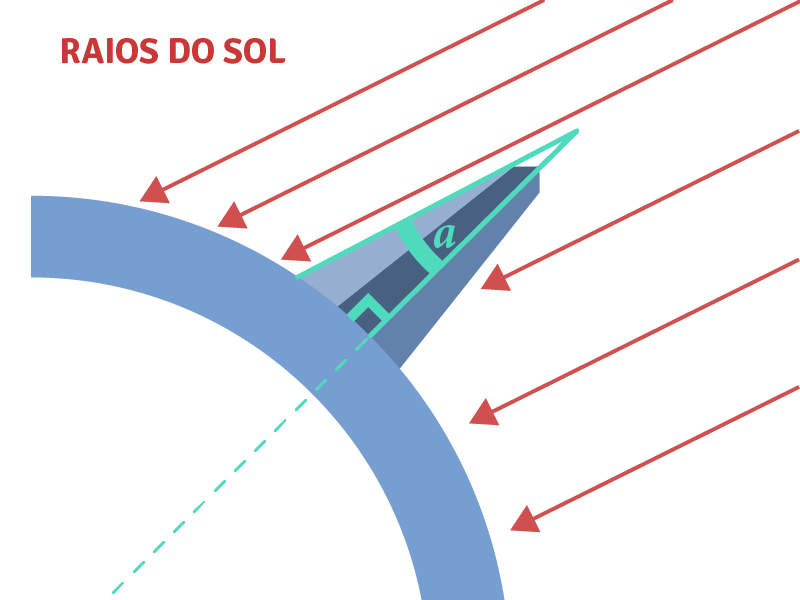
Como ele sabia que a altura da madeira que tinhaposto no chão e o comprimento da sombra,pode determinar a extensão do ângulo , naquela hora.
Agora, assumindo, assim como fez Eratóstenes, que o sol está longe o suficiente da Terra, podemos supor que os raios do sol que chegam à Alexandria são paralelos aos raios do sol que atingem Siena. Representamos essa situação da seguinte forma:
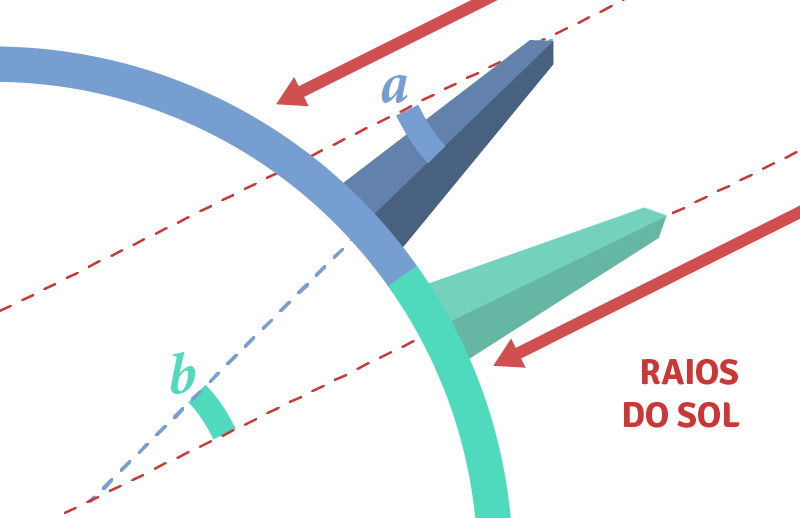
Você se lembra do princípio geométrico que vimos no início do artigo? Veja que as condições de paralelismo descritas são atendidas neste caso: os raios do sol que passam por Alexandria e Siena desempenham o papel de retas paralelas. Além disso, podemos imaginar que o pedaço de madeira de Eratóstenes forma uma reta que corta as duas paralelas, fazendo com que os ângulos e sejam internos alternados, e, portanto, que tenham a mesma medida.
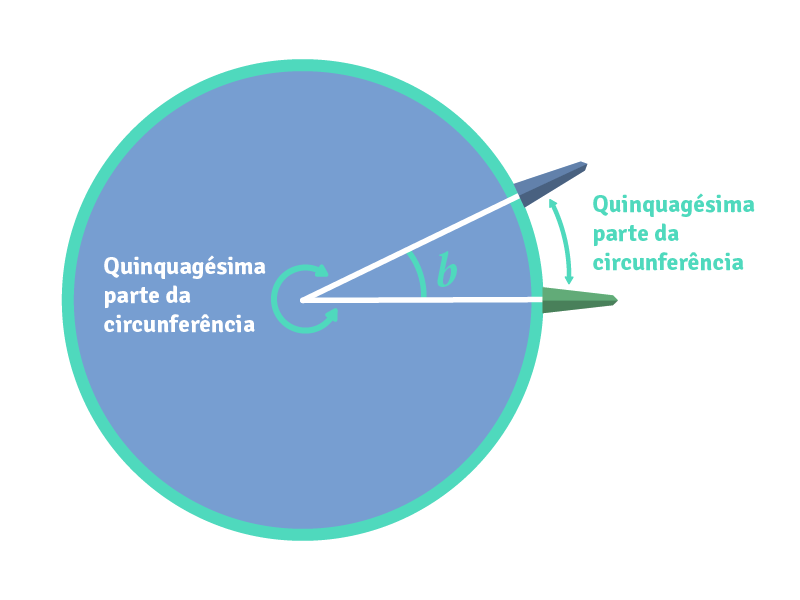
Como ele já tinha calculado a medida do ângulo , tinha também a medida do ângulo , cuja vértice é o centro da terra, assim o arco é a distância da cidade de Siena até Alexandria. Quando ele mediu o ângulo (que é igual a medida de ), descobriu que era cerca de uma quinquagésima parte de toda a circunferência, que mede ( .
Portanto, a distância entre Alexandria e Siena também deveria ser de uma quinquagésima parte da circunferência da Terra. Desta forma se ele pudesse saber a distância entre Siena e Alexandria, apenas teria que multiplicar isso por cinquenta e o resultado seria a medida da circunferência da Terra
Com o seu próprio dinheiro Eratóstenes pagou para medir a distância entre as duas cidades, alguns dizem que quem fez isso foi uma caravana de comerciantes, outros falam de militares, e outros que um dos seus servos caminhou de uma cidade para outra contando passo por passo. De qualquer forma, Eratóstenes sabia, pelo menos aproximadamente, a distância entre Alexandria e Siena.
Depois de realizar os cálculos, Eratóstenes concluiu que a circunferência da Terra era aproximadamente de estádios, unidade de medida usada naquele tempo na Grécia. Neste ponto há uma controvérsia, alguns historiadores dizem que Eratóstenes usou o estádio ático-italiano, o que resultaria em uma aproximação de km. Outros dizem que ele usou o estádio egípcio, o que daria uma aproximação de km. Em qualquer caso, são realmente boas aproximações considerando que a ciência moderna aceita 40.008km como circunferência do planeta. Um erro quase insignificante considerando a precariedade dos instrumentos de medição que ele usou para fazer suas estimativas.
Eu conheci essa incrível história há muitos anos e sempre que posso compartilho com meus alunos. Acho que é um exemplo vivo do poder do pensamento humano e das possibilidades que o homem tem e que vão além de suas limitações físicas. Eratóstenes não precisou andar um centímetro na superfície da Terra e ainda a conseguiu medir com sua sabedoria. E tudo com um pequeno pedaço de pau preso no chão!
/pt/usando-a-matematica/mas-e-se-o-sol-fosse/content/