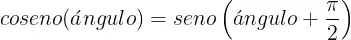Probado en Node.js:
var Log = require( 'console' ).log;
function point( min ) {
var rad = 2 * Math.PI * ( min / 60 ) - ( ( 2 * Math.PI ) / 4 );
return [ Math.cos( rad ), -Math.sin( rad ) ];
}
Log( point( 0 ) );
Log( point( 15 ) );
Log( point( 30 ) );
Log( point( 45 ) );
Log( point( 60 ) );
EDITO
Explicación detallada del meollo del asunto: var rad = 2 * Math.PI * ( min / 60 ) - ( ( 2 * Math.PI ) / 4 );
2 * Math.PI * ( min / 60 )
Transformamos los minutos en radianes. ( min / 60 ) nos resulta en los grados equivalentes a los minutos indicados. Para convertirlo en radianes (las funciones matemáticas implicadas, Math.sin y Math.cos, trabajan con radianes, no con grados), se multiplican por 2Pi.
- ( ( 2 * Math.PI ) / 4 )
Las funciones seno y coseno son funciones periódicas, con resultados comprendidos entre -1 y 1, ambos incluidos ( [-1, 1] ). Esa expresión prepara el anterior resultado ( el angulo en radianes que estamos procesando ) para que las salidas de Math.sin() y Math.cos() nos resulten útiles. Digamos que escala los radianes para que el resultado de Math.sin() y Math.cos() encajen en nuestro espacio completo de la circunferencia.
EDITO 1 para adecuarlo a la nueva versión de la pregunta.
Explicación de porque es posible esa sustitución
Como dije anteriormente, seno( ) y coseno( ) son funciones periodicas, es decir, sus valores se repiten con el tiempo. Lo que no dijimos es su periodo, lo que tardan en repetir sus valores. En ambos casos, su periodo es PI / 2.
Pensemoslo con detenimiento ... mismo rango de valores de resultado ... mismo periodo ... esto nos sugiere que ambas funciones han de ser muy similares, variando unicamente el desplazamiento sobre el eje X del resultado.
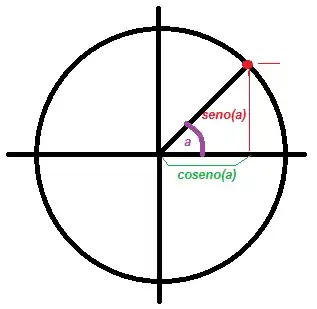
En esta gráfica tan chula, tomada de la Wikipedia, se aprecia todo muy bien. El eje X representa el angulo en radianes, mientras que el eje Y representa la salida de la función (el valor que devuelve).
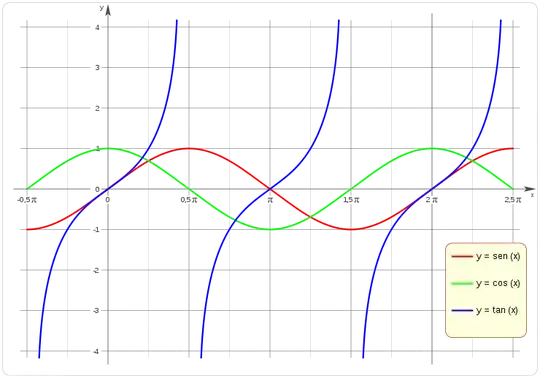
Fuente: Wikipedia, Trigonometría
Si miramos la gráfica, lo vemos todo claro:
El coseno de un ángulo (línea verde), no es más que el seno (línea roja) del mismo angulo desfasado PI/2 radianes; es decir, el coseno va por detrás; en un momento dado cualquiera, siendo X el seno de un angulo A, el coseno es exactamente el mismo que el seno de ( A - ( PI / 2 ) ), ambos en radiantes.
En la gráfica, se aprecia claramente que seno( PI ) == 0, que es exactamente coseno( PI / 2 ) == 0. Igual para los demás valores. Si lo hacemos en grados, el coseno va 45º por detrás del seno.
A continuación, puesto que la gráfica no tiene apenas valores, muestro algunos, para comprobarlo:
Grados: 0, radianes: 0, seno: 0, coseno: 1
Grados: 45, radianes: 0.7854, seno: 0.8509, coseno: 0.7071
Grados: 90, radianes: 1.5708, seno: 0.894, coseno: 0
Grados: 135, radianes: 2.3562, seno: 0.0884, coseno: -0.7071
Grados: 180, radianes: 3.1416, seno: -0.8012, coseno: -1
Grados: 225, radianes: 3.927, seno: -0.9301, coseno: -0.7071
Grados: 270, radianes: 4.7124, seno: -0.176, coseno: 0
Grados: 315, radianes: 5.4978, seno: 0.7451, coseno: 0.7071
Grados: 360, radianes: 6.2832, seno: 0.9589, coseno: 1
EDITO 2
¿ Porqué no coinciden los valores ? según la parrafada de antes, deberían coincidir, ¿ no ?
Recomiendo hechar un ojo a ¿Por qué mis programas no pueden hacer cálculos aritméticos correctamente?
En esta tabla de ejemplo, además de lo anterior, y como veremos en el código, parte de la culpa la tiene el uso de la función Number.toFixed( ), que descarta decimales. En este caso concreto, no ocurre nada, pero... si tenemos que escalar el resultado (multiplicarlo por algún número), la imprecisión puede ser suficientemente grande como para producir artefactos no deseados, sobre todo en temas gráficos.
FIN EDITO 2
El código en Node.js, muy simple, por si alguien quiere comprobarlo:
var log = require( 'console' ).log;
var grad,
rad;
for( grad = 0; grad < 365; grad += 45 ) {
rad = grad * Math.PI / 180;
log( "Grados: %d, radianes: %d, seno: %d, coseno: %d", grad, rad.toFixed( 4 ), Math.sin( grad ).toFixed( 4 ), Math.cos( rad ).toFixed( 4 ) );
}
Se aprecia que cos( 90º ) == 0, que es exactamente lo mismo que sen( 0 ) == 0; Lo dicho anteriormente, el coseno de un angulo es el seno de angulo - PI/2; o, dicho de otra forma, el coseno var 45º por detrás.
Ya sabemos porqué es posible esa sustitución.
Respuesta a la nueva pregunta.
Hablo por mí, los demás tendrán sus propias razonas. Usé el coseno porqué es lo que viene en todos los ejemplo que he visto en Internet. No se me ocurrio hacerlo asi, sin el coseno ;-)
EDITO 2
Teniendo en cuenta el tema de la precisión numérica expuesto mas arriba, resulta que si hay un motivo para usar el coseno.
Pensemos:
- ángulo X -> impreciso.
- PI -> impreciso.
Entonces, coseno( X ) tendrá mas precisión que seno( X - ( PI / 2 ) ), por el sencillo motivo de que lo segundo usa 2 números imprecisos pare realizar el cálculo, lo cual aumentará la imprecisión de la salida.
¡ Que cosas !